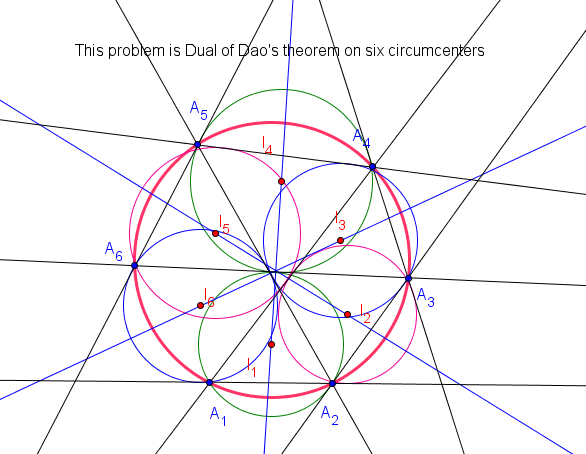
Mở rộng định lý Lester, định lý Parry, định lý Zeeman-Gossard

Một giả thuyết giống định lý Cayley–Bacharach

Giả thuyết 1: Cho sáu điểm $A, A', B, B', C, C'$ cùng nằm trên một đường bậc hai và đường bậc ba (nào đó). Cho một đường bậc hai đi qua $B, B', C, C'$ và cắt đường bậc ba đó tại $A_1, A_2$. Đường bậc hai đi qua $C, C', A, A'$ và cắt đường bậc ba đó tại $B_1, B_2$. Đường bậc ba đi qua $A, A', B, B'$ và cắt đường bậc ba tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường bậc hai. Nếu ta chọn trước các điểm $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng phải thẳng hàng.

Giả thuyết 2: Cho một đường conic cắt một đường bậc ba tại 6 điểm $A, B, C, D, E, F$. Cho một đường conic khác đi qua ba điểm $A,B,C$ cắt đường bậc ba tại $G, H, I$, cho đường conic khác đi qua ba điểm $D, E, F$ cắt đường bậc ba tại $J, Q, K$. Khi đó sáu điểm $G, H, I, J, Q, K$ sẽ nằm trên một đường conic.

Chứng minh giả thuyết 2:
Đây là cách chứng minh cho giả thuyết 2 của một giáo sư (mà mình không hiểu) nhưng cứ trình bày lại ra đây để mọi người tham khảo: 

Áp dụng luật nhóm, nếu như một đường bậc hai giao với một đường bậc ba tại sáu điểm thì tổng sáu điểm phải bằng không. Ta có A+B+C+D+E+F=0; A+B+C+G+H+I=0; D+E+F+J+Q+K=0 => G+H+I+J+Q+K=0 => Sáu điểm G, H, I, J, Q, K nằm trên một đường conic. Giả thuyết mạnh hơn được chứng minh.

Giả thuyết tổng quát: Cho hai đường cong (đa thức) cắt nhau tại $\frac{d^2+3d}{2}+\frac{l^2+3l}{2}+2$ điểm. Nếu $\frac{d^2+3d}{2}+1$ điểm nằm trên đường cong bậc $d$ thì $\frac{l^2+3l}{2}+1$ điểm còn lại sẽ nằm trên đường cong bậc $l$

Giả thuyết: Cho sáu điểm $A, A', B, B', C, C'$ nằm trên một đường conic. Đường conic qua bốn điểm $B, B', C, C'$ cắt đường thẳng $AA'$ at $A_1, A_2$. Đường conic qua bốn điểm $C, C', A, A'$ cắt đường thẳng $CC'$  tại $B_1, B_2$. Đường conic qua bốn điểm $A, A', B, B'$ cắt đường thẳng $CC'$ tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường conic. Do đó nếu chọn trước $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng thẳng hàng.

Mở rộng định lý Pascal và định lý Brianchon

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn.

2. Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

http://tube.geogebra.org/m/1539785

TẠI SAO TÔI PHÁT HIỆN RA KẾT QUẢ NÀY?

Định lý Pascal là một định lý nổi tiếng đặt theo tên nhà bác học Blaise Pascal (1623-1662). Nội dung như sau:

Cho một lục giác nội tiếp khi đó giao điểm của các cặp cạnh đối diện nằm trên một đường thẳng.

Ngày 29/08/2015 anh Nguyễn Ngọc Giang có đăng trên facebook một kết quả là mở rộng của định lý Pascal như sau:



Tôi nhìn vào cách mở rộng của anh Giang tôi thấy rằng sẽ có một lục giác đối xứng với đường tròn ngoại tiếp lục giác $ABCDEF$ ban đầu ở bên kia trục của đường thẳng d. Với kinh nghiệm "CHƠI" hình học phẳng mấy năm nay tôi hiểu rằng kết quả này có thể mở rộng thành một định lý tổng quát hơn bằng cách ta thay lục giác đối xứng đó trong kết quả của anh Giang bằng một lục giác nội tiếp bất kỳ, ở vị trí bất kỳ trong mặt phẳng. Tôi nghĩ như vậy và tôi kiểm tra qua phần mềm thấy ý tưởng của tôi hoàn toàn đúng đắn. Quan sát kỹ hơn tôi thấy rằng cấu trúc hình học này thực ra tôi đã tìm ra và đăng trên tạp chí Crux vào tháng 5/2014(mà tôi vẫn gọi là vấn đề (hoặc định lý) tám đường tròn. Vốn được tôi biết đến như là một mở rộng của định lý Brianchon (một định lý kép của định lý Pascal).

Nội dung mở rộng định lý Pascal và định lý Brianchon như sau:

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Mở rộng định lý Pascal: Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn (1)

Khi nào đường tròn này suy biến thành đường thẳng Pascal? Ở đây tôi chỉ ra hai cách để đường tròn này suy biến thành đường thẳng Pascal như sau:

Cách 1: Xây dựng như cách của anh Giang.

Cách 2: Nếu cho đường tròn qua $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm đặt tên là điêm $M$, khi đó rõ ràng $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$ đều đi qua $M$. Giả sử các giao điểm còn lại của của $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ là $A, B, C$ như vậy theo kết quả (1) $A, B, C, M$ nằm trên một đường tròn. Bây giờ nếu ta cho điểm M cứ tiến tới vô cùng khi đó đường tròn này sẽ biến thành một đường thẳng và $A, B, C$ chính là giao điểm của ba cặp cạnh đối diện của lục giác $A_1A_2A_3A_4A_5A_6$.

2. Mở rộng định lý Brianchon: Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

Khi nào kết quả trên thu về định lý Brianchon? Ở đây tôi chỉ ra hai cách để kết quả trên suy biến thành định lý Brianchon.

Cách 1: Dựng hình sao cho các điểm Ai trùng với Ai' khi đó sẽ có phát biểu là:

Cho sáu đường tròn  $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$, giả sử các đường tròn $(O_i)$ tiếp xúc $(O_{i+1})$ (chúng ta lấy Modulo 6) và sáu điểm tiếp xúc này nằm trên một đường tròn khi đó đường thẳng  $O_1O_4, O_2O_5, O_3O_6$ đồng quy. Thực sự dễ dàng thấy rằng định lý Brianchon là trường hợp đặc biệt của kết quả này.

Cách 2: Cho $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm (trùng nhau) đặt tên là điểm $M$ cho điểm này trùng với tâm đường tròn ngoại tiếp $A_1A_2A_3A_4A_5A_6$  sau đó vị tự tỉ số 2 ta sẽ có ngay định lý Brianchon.

Cho một đường conic $S$ và điểm $P$ trên mặt phẳng, ba đường thẳng qua P cắt conic lần lượt cắt đường conic tại các điểm $A, A'; B, B'; C, C'$. Nếu $D$ nằm trên đường thẳng cực của $P$ hoặc $D$ nằm trên đường conic thì $A'D, B'D, C'D$ lần lượt cắt ba cạnh $BC, CA, AB$ tại ba điểm $A_0, B_0, C_0$ thẳng hàng. Hơn thế bốn điểm $A_0, B_0, C_0, P$ thẳng hàng khi và chỉ khi $D$ nằm trên đường conic.

Kết quả trên là mở rộng của các định lý sau:

1. Định lý Droz-Farny,

2. định lý Goormaghtigh,

3. định lý đường thẳng Đào (hẹp),

4. định lý Zaslavsky,

5. định lý Colling,

6. định lý Simsson,

7. Vấn đề Adam Bliss

Kết quả trên được chứng minh trong các bài báo của:

* Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, Vol.4, (2015), Issue 2, page 102-106
* Son Tran Hoang (2014), A synthetic proof of Dao's generalization of Goormaghtigh's theorem. Global Journal of Advanced Research on Classical and Modern Geometries, volume 3, pages 125–129, ISSN 2284-5569

* O.T.Dao 2013, Two Pascals merge into one, Cut-The-Knot

* Geoff Smith (2015). 99.20 A projective Simson line. The Mathematical Gazette, 99, pp 339-341. doi:10.1017/mag.2015.47
 

Vấn đề: Dual của định lý Đào về sáu tâm đường tròn ngoại tiếp (đây là đường tròn nội tiếp).

Cho một lục giác nội tiếp, khi đó đường thẳng nối tâm các đường tròn nội tiếp các tam giác tạo bởi hai cạnh và chung đường chéo chính sẽ đồng quy.

http://tube.geogebra.org/m/1488371

Dual của định lý Maxwell.

Cho tam giác $ABC$, và đường thẳng $L$. Đường thẳng $L$ cắt ba cạnh $BC, CA, AB$ tại $A_1, B_1, C_1$. Gọi $A'B'C'$ la tam giác trong mặt phẳng đó sao cho $B'C', C'A', A'B'$ là song song với $AA_1, BB_1, CC_1$. Chứng minh rằng ba đường thẳng đi qua  $A', B', C'$ và lần lượt song song với $BC,CA,AB$ sẽ cắt ba cạnh $B'C', C'A', A'B'$ tại ba điểm thẳng hàng.

Mở rộng định lý Sondat:

Cho tam giác $ABC$, cho $P$ là một điểm bất kỳ trên mặt phẳng, cho đường thẳng $d$ cắt ba cạnh tam giác tại $A_0$, $B_0$, $C_0$ ba đường thẳng tương ứng qua $A_0,B_0,C_0$ và song song với $AP, BP, CP$ tạo thành tam giác $A_1,B_1,C_1$. Theo định lý Maxwell thì ba đường thẳng qua $A_1, B_1, C_1$ và song song với $BC,CA,AB$ một cách tương ứng lại sẽ đồng quy tại một điểm ta gọi điểm này là $P_1$. Khi đó đường thẳng $d$ chi đôi đoạn thẳng $PP_1$. Trong trường hợp $P$ là trực tâm vấn đề này là định lý Sondat.

http://tube.geogebra.org/m/1467027

https://groups.yahoo...s/messages/2673

Phiên bản cuối cùng của giả thuyết

Giả thuyết của anh không đúng, thử với $95800^4+217519^4+414560^4=422481^4$ (R. Frye 1988).

Thực ra, năm 1967, L. J. Lander, T. R. Parkin, and John Selfridge đã đưa ra một giả thuyết, mở rộng cho định lý Fermat lớn:

 

Nếu $k>3$ và $\sum_{i=1}^{n}a_i^k= \sum_{i=1}^mb_j^k$ trong đó $a_i \ne b_j$ với mọi thì $1 \le i \le n, 1 \le j \le m$ có nghiệm nguyên dương thì $m+n \ge k$.

 

Anh có thể xem thêm tại Euler's sum of powers conjecture.

 

Giả thuyết của anh chắc có thể đúng nếu chỉnh điều kiện từ $k \ge m+n$ thành $k>m+n$.

Cảm ơn em. Giáo sư Đào Hải Long cũng cho anh biết thông tin trên, và đưa đường link :

https://en.wikipedia...idge_conjecture

1. Quan sát:
 

Cho hai hàm số liên tục $f(x)$ và $g(x)$ với $x \in [a,b]$, khi đó khả năng tồn tại một giá trị $x_0$ thực để $f(x_0)=g(x_0)$ là cao hơn so với khả năng tồn tại giá trị nguyên $y_0$ để $f(y_0)=g(y_0)$. Điều này dễ dàng hình dung qua đồ thị về giao điểm của hai hàm số liên tục và giao điểm của hai hàm số rời rạc. Đối với một đa thức khi bậc của đa thức cao lên thì độ rời rạc của đa thức $f(x)$ ($x$ nguyên) càng cao và dẫn đến giá trị $f(x)+f(y)=f(z)$ với $x,y,z$ nguyên càng trở lên khó khăn. Theo chiều hướng đó khi bậc của đa thức $k$ tăng đến một mức độ nào đó thì sẽ dẫn đến phương trình $f(x)+f(y)=f(z)$ hoàn toàn trở lên vô nghiệm. Xuất phát từ nguyên lý đó tôi đưa ra một giả thuyết như sau(chú ý giả thuyết sau chỉ là một cách để cố gắng thể hiện kết quả trong quan sát trên):

2. Giả thuyết: Cho $a$ là một số nguyên khác $0$, $m,n$ là hai số nguyên dương khác nhau, $g(x)$ là một đa thức bất kỳ cho trước, đặt $f(x)=g(x)+ax^k$, khi đó tồn tại một hằng số nguyên dương $k_0$ để với mọi $k \geq k_0$ thì phương trình:
$$f(x_1)+f(x_2)+....+f(x_n)=f(y_1)+....+f(y_m)$$
không có nghiệm nguyên dương khác một.

Chú ý: Tôi thêm chữ khác 1 vào để loại bỏ trường hợp tầm thường cho phù hợp với ý tưởng xuất phát là độ rời rạc của đa thức tăng lên khi bậc của đa thức tăng lên vì với x=1 thì f(1) không thay đổi khi ta chỉ thay đổi bậc của đa thức. Ngoài ra phản biện tại #2 của Zaraki là cho phiên bản version 1

 

Bạn Quang Dương có hỏi tôi về việc chứng minh phương trình sau có nghiệm trong khoảng $(-\pi,\pi)$.

$\cos 2x+\cos x.(2-\cos  a-\cos b)+\sin x.(\sin a+\sin b)+1-\cos a-\cos b=0$, trong đó $x$ là ẩn và $a,b$ là tham số.

Theo tôi thì cách làm thông thường như biết đổi lượng giác, quy về phương trình đa thức.... có thể sẽ bế tắc.

Lời giải cho vấn đề tám đường tròn, Proposed by Đào Thanh Oai, solution by Luis Gonzalez

Cách xác định $A_1$ còn mờ ám. Vì có hai vị trí $A_1$ (vị trí còn lại nằm ở cung đối diện). Tương tự với $B_1,C_1,...$

Thực ra anh cũng nhận ra điều đó(nhưng lười viết), cảm ơn em nhé. Anh bổ sung như sau:

Nếu đường tròn $A_1$ như hình vẽ thì tất cả các đường tròn Thebault tương ứng với $B_1,C_1,...,F_1$ còn lại như hình vẽ.
Nếu đường tròn tương ứng với $A_1$ phía đối diện thì tất cả các đường trờn tương ứng với $B_1,C_1,...,F_1$ cũng nằm ở phía đối diện
Nếu đường tròn tương ứng với $A_1$ nằm ngoài thì tất cả các đường tròn tương ứng $B_1,C_1,...,F_1$ cũng năm phía ngoài.(nằm ngoài cũng có hai trường hợp)

 

Vấn đề mở rộng định lý Feuerbach–Luchterhand

Vấn đề được nêu trong file đính kèm

 June-14-2014-Feuerbach-Luchterhand.pdf   106.14K   544 Số lần tải

Vấn đề của một lục giác lồi nội tiếp và sáu đường tròn Thebault.

Cho lục giác $ABCDEF$ lồi nội tiếp đường tròn $(O)$. Gọi $A_1,B_1,C_1,D_1,E_1,F_1$ lần lượt là các tiếp điểm chung của sáu đường tròn Thebault $(FA,BC,(O))$, $(AB,CD,(O))$, $(BC,DE,(O))$, $(CD,EF,(O))$, $(DE,FA,(O))$, $(EF,AB,(O))$ với $(O)$. Hãy chứng minh $A_1D_1, B_1E_1, C_1F_1$ đồng quy.

http://tube.geogebra.org/m/1352263

Hình vẽ của mở rộng định lý Lester(#20).

Ký hiệu trong hình vẽ. $X_4$ là trực tâm, $X_{3}$ là tâm ngoại tiếp, $X_{13}$, $X_{14}$ là hai điểm Fermats

Mở rộng đường tròn Lester với đường Neuberg cubic.

Đường Neuberg cubic: Cho tam giác $ABC$, một điểm $P$ là điểm trên đường Neuberg cubic của  $ABC$ nếu thỏa mãn với $P_a,P_b,P_c$ là ba điểm đối xứng của $P$ qua ba cạnh $BC,CA,AB$ thì $AP_a, BP_b, CP_c$ sẽ đồng quy tại một điểm, ta gọi điểm này là $Q$. 

Mở rộng định lý đường tròn Lester: Bốn điểm gồm 2 điểm Fermat, P, Q được định nghĩa như trên nằm trên một đường tròn.

Với không gian hai chiều $f(n,m)=\frac{n}{m}=\frac{n}{2}$ 

Giả thuyết trên được chúng tôi phát triển từ bất đẳng thức quen thuộc trong hình học tam giác:

$\sin A.\sin B. \sin C \leq 3.\sqrt{3}/8$

Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114.

 FG201509.pdf   94.99K   458 Số lần tải

Liên quan đến định lý lá cờ Anh viết cùng thầy Nguyễn Minh Hà

 La co nuoc Anh.pdf   356.99K   1274 Số lần tải

Dao Thanh Oai, A family of Napoleon triangles associated with the Kiepert configuration, The Mathematical Gazette, Published online: 13 March 2015

http://journals.camb...d=0&issueId=544

 TamgiaNapoleon.pdf   309.59K   479 Số lần tải