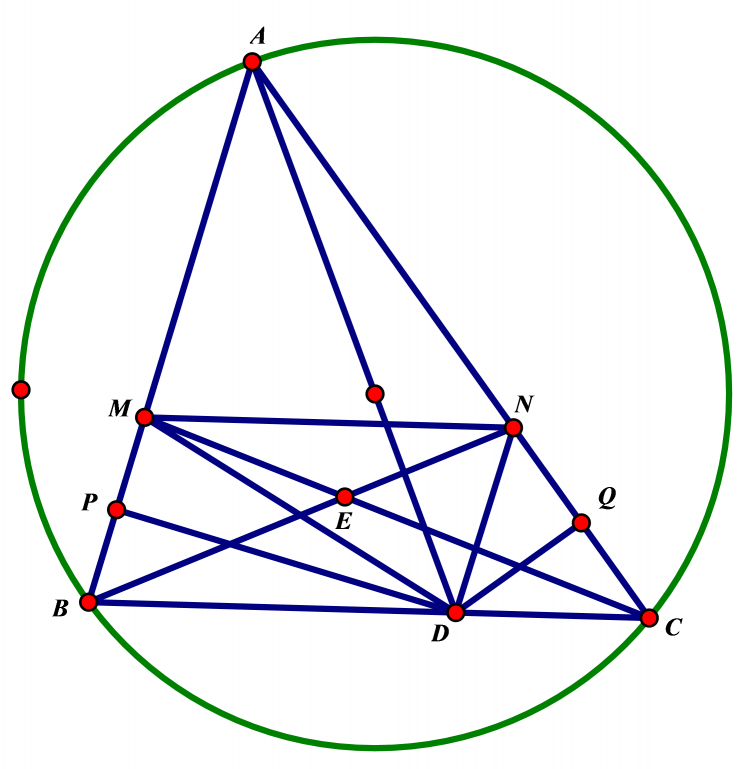
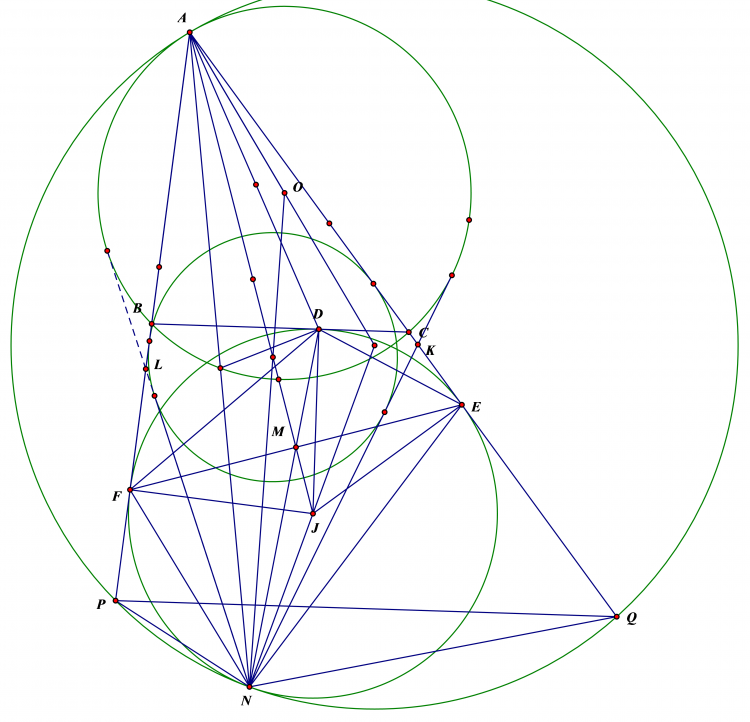
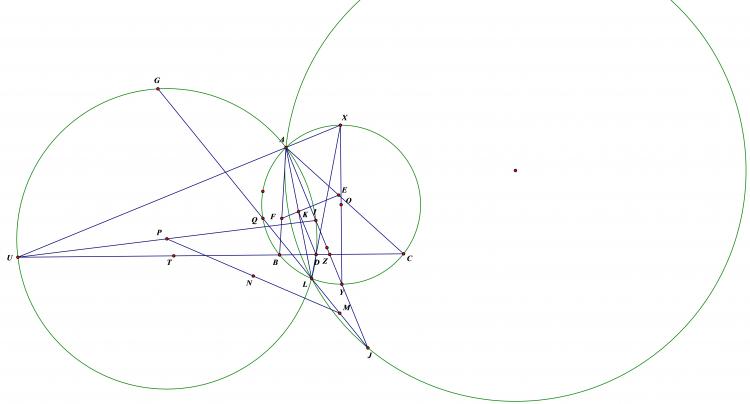
Tam giác ABC nhọn, H trực tâm. Tiếp tuyến tại A với đường tròn ngoại tiếp tam giác ABC cắt BC tại P. Từ P kẻ tiếp tuyến PQ đến (HBC). H và Q nămf cùng phía trên mặt phẳng bờ BC.Chứng minh rằng góc HQA là góc vuông

Gọi $K$ là tâm $HBC$ , suy ra $\Delta PQK=\Delta PAO$ nên $\Delta PAQ$ đồng dạng $\Delta POK$ 

Ta có :$\widehat{HAQ}=\widehat{QAP}-\widehat{HAP}=\widehat{KOP}+90^0-(\widehat{C}-\widehat{B})=180^0-(\widehat{C}-\widehat{B})-\widehat{OPB}=\widehat{APO}$

Và $\frac{AQ}{AP}=\frac{OP}{OK}=\frac{OP}{AH}$

Tứ 2 điều trên suy ra $\Delta APO$ đồng dạng $\Delta QAH$ nên  $HAQ$ vuông tại $Q$

Có thể trình bày chi tiết ra dùm mình được ko?

Đưởng thẳng nổi trực tâm của tam giác $BEM,CEN$ chính là đường thẳng Steiner của tứ giác toàn phần $AMEN.BC$ , Ta chỉ cần chứng minh $AE$ là đường thẳng Gauss của tứ giác toàn phần đó là được , để chứng minh điều đó , ta chứng minh $AE$ đy qua trung điểm $BC$ , tức là cần chứng minh $MN$ song song $BC$ , 

Gọi $P,Q$ là trung điểm $BM,CN$ khi đó$\frac{BM}{CN}=\frac{BP}{CQ}=\frac{Cos\widehat{B}.BD}{CD.Cos\widehat{C}} =\frac{Sin\widehat{OAC}.DB}{Sin\widehat{OAB}.DC}=\frac{AB}{AC}$ thì $MN$ song song $BC$ có dpcm

 Lời giải :

+Ta có bổ đề sau : Cho $(O),(C),(D)$ với $(C),(D)$ tiếp xúc trong với $(O)$ tại $A,B$ , Kẻ $BX,BY$ tiếp xúc với $(C)$ . $AZ,AT$ tiếp xúc với $(D)$ , Chứng minh 4 đường $BX,BY,AZ,AT$ tạo thành tứ giác ngoại tiếp

Giải : $AD$ cắt $BC$ tại $G$ , ta sẽ chứng minh $AEBF$ ngoại tiếp tâm $G$ ,( $E,F$ như hình vẽ ) gọi $r_{1},r_{2}$ là khoảng cách từ $G$ đến $BY,AZ$

Ta có :$\frac{r_1}{r_2}=\frac{BG.AC}{BC}:\frac{AG.BD}{AD}=\frac{BG}{AG}.\frac{AC}{BC}.\frac{AD}{BD}=1$ suy ra$r_{1}=r_{2}$ nên $(G,r_1)$ nội tiếp $AEBF$

+Trở lại bài toán : ta sẽ chứng minh $AN,AD$ đẳng giác trong góc $BAC$ , tức $AN$ sẽ đy qua tiếp điểm $A-Mix$ với $(O)$

- Nghịch đảo tâm $A$ phương tích bất kì ta có bài toán sau : tam giác $ABC$ nt $(O)$ , $(J)$ là $A-Mix$ tx $(O)$ tại $D$ , $(ADJ)$ cắt $(J)$ tại $N$ , khi đó $AN,AD$ đẳng giác ( điều này đúng do $JD=JN$) suy ra $AN$ sẽ đy qua tiếp điểm $A-Mix$ với $(O)$

-  Xét phép vị tự tâm $A$ biến $A-Mix \mapsto (J)$... $B,C \mapsto Q,P$ như hình vẽ , Khi đó $(J)$ sẽ là đường tròn $Mixtilinear$ của tam giác $APQ$ 

Áp dụng bỏ đề với $(J)$ và $(ABC)$ cùng tiếp xúc trong với $(APQ)$ nên ta có $AKNL$ ngoại tiếp.

Bài 172 (sáng tác từ một bài toán của bạn Bảo ) : Cho tam giác $ABC$ cố định có đường cao $AH$ , $P$ di chuyển trên tia đối của tia $HC$ , $M$ đối xứng với $C$ qua $H$ . $MN$ song song với $AC$ với $N$ thuộc $AP$ . $Q$ là trung điểm $AH$ . $PQ$ cắt $HN$ tại $D$. Đường tròn $(X)$ thay đổi qua $D$ và tiếp xúc với đường tròn euler của tam giác $AHD$ cắt $DA,DH$ tại $F,E$ . Chứng minh : $(XFE)$ tiếp xúc với đường thẳng cố định khi $P$ và $(X)$ thay đổi

Bài 171 : ta có $A(ROHM)=-1$ , Gọi $I$ là trung điểm $H$ thì $OI$ vuông góc $AG$ ,$OH$ cắt $AM$ tại $K$ thì $O$ là trung điểm $HK$ , mà $A(ROHM)=-1$ nên $AR$ song song $OH$

Hạ $ME,AF$ vuông góc với $AD,IM$ . $AF,ME$ cắt nhau tại $K$ , có $A(FE,PN)=-1$ nên $ENFP$ là tứ giác điều hòa nên $\frac{FP}{FN}=\frac{EP}{EN}$

mặt khác , dễ thầy , $I$ là trực tâm tam giác $AMK$ do đó $(IFKE)$ trực giao với $(AM)$ tức $(AFNEMP)$ mà $\frac{FP}{FN}=\frac{EP}{EN}$

Nên $(IEF)$ là đường tròn $(F-Apolo)$ của tam giác $FPN$ nên$\frac{IP}{IN}=\frac{EP}{EN}=\frac{Sin\widehat{PAI}}{Sin\widehat{NAI}}$ 

=> bán kinh $(AIP)=(AIN)$ nên $\widehat{IPA}=\widehat{INA}=>\widehat{IPM}=\widehat{INM}$

Hạ $IX,IY$ vuông góc với $MP,MN$ khi đó $IX,IY$ đẳng giác góc $PIN$

Bây giờ , ta thấy , phân giác $PMN$ song song pg góc $BAC$ do $ANMP$ đồng viên đường kính $AM$

Mặt khác pg góc $BAC$ song song pg $XIY$ do có các cặp cạnh song song , Mà pg góc $XIY$ chính là pg góc $PIN$ do $IX,IY$ đẳng giác góc $PIN$

Lời giải:

Phân giác ngoài góc $A$  của tam giác $ABC$ cắt $BC$ tại $T'$ . $O'$ là điểm chính giữa cung nhỏ $BC$ , $T'O'$ cắt $AB,AC$ tại $P',Q'$

 

Dễ nhận thấy các điều sau : $O$ là điểm chính giữa cung nhỏ $KL$ của $(AKL)$ và $AT$ là phân giác ngoài góc $A$ của tam giác $AKL$

 

Phép vị tự tỉ số $\frac{AB}{AK}$ tâm $A$ hợp phép quay góc $(AK,AB)$ tâm $A$ biến lần lượt :$K,L,O,T,P,Q \mapsto B,C,O',T',P',Q'$

 

Suy ra $APP'$ cân tại $P$ nên $F$ là trung điểm $AP'=>$$\widehat{NVU}=\widehat{BMP'}$  nên ta cần chứng minh $\widehat{BMP'}=\widehat{CMQ'}$

 

Điều này đúng do $M(T'O',P'Q')=-1$ với $O'M$ vuông góc với $MT'$ suy ra $\widehat{BMP'}=\widehat{CMQ'}$ . Vậy nên tam giác $NUV$ cân tại $N$

tam giác $BMA,CNA$ cân tại $B,C$ nên nếu $J$ là tâm bàng tam giác $ABC$ thì $J$ là tâm ngoại $(AMN)$

Theo bổ đề quen thuộc thì $ED$ vuông góc $JO$ , mặt khác $JO$ lại vuông góc với $AF$ nen $AF$ ss $ED$

Bài này chứng minh $AE$ là đường thẳng GAUSS của tứ giác toàn phần $AMEN.BC$ tức là $AE$ đy qua trung điểm $BC$ , hay việc chứng minh đưa về chứng minh $MN$ song song $BC$ , đến đây bạn có thể tính toán tùy ý :v , mình thì mình dùng lượng giác , cũng tàm tạm

Nham . ss voi $BC$

Từ $D$ kẻ dg thẳng ss $AB$ cắt $(O)$ tại $K$ thì $KEAF,KBAC$ là tứ giác điều hòa do đó . tiếp tuyến tại $A$ . $EF,BC$ đồng quy tại $H$ suy ra $HA^2=HE.HF=HT^2$ nên $AT$ là pg giác góc $BAC$ nên $AT$ đy qua đ chính giữa cung $BC$

Em có lời giải sau :

Bổ để : cho $(I),(O)$ trực giao nhau và cắt nhau tại $B,C$ , $D$ thuộc cung nhỏ $BC$ của $(I)$ , $DB$ cắt $(O)$ tại $F$ , $FO$ cắt $(O)$ tại $E$ thì $E,D,C$ thẳng hàng

Chứng minh , Gọi $CF$ cắt $(I)$ tại $A$ , áp dụng Pascal cho bộ $\binom{ABC}{DCB}$ suy ra dpcm

Trở lại bài toán : $BE$ cắt $CF$ trên $(O)$ tại $H$ , ta có  :$H(AQEF)=-1$ nên $HQ$ cắt $(O)$ tại $K$ thì $ABKC$ là tứ giác điều hòa nên $AK$ đối trung , $K$ cố định

Tiếp theo ta sẽ chứng minh $R$ thuộc $HK$ , ta có $\frac{AB}{AC}=\frac{Sin\widehat{BPR}}{Sin\widehat{CPR}}=\frac{BR}{CR}$ ( dó 2 bán kính đường tròn $(BRP),(CRP)$ bằng nhau ) nên $R$ thuộc $(Apolo)$ dựng trên $BC$ và qua $A$ , Mặt khác $(Apolo),(O)$ trực giao nhau nên theo bổ để , $R,H,K$ thẳng hàng

Vậy $RQ$ đy qua $K$ cố định

Em có ý tưởng khác như sau

$AI$ cắt $(I)$ tại $J,Y$. $DJ$ cắt phân giác ngooài góc $\widehat{BAC}$ tại $X$ . khi đó $(AXYD)$ thuộc đường tròn đường kính $XY$,

mặt khác ,$\widehat{MDY}=\widehat{EJY}=\widehat{MAY}$ và tương tự suy ra $ADMNXY$ cùng thuộc đường tròn đường kính $XY$ . 

Nhận thấy $AY$ là phân giác $\widehat{MAN}$ nên $XY$ là trung trực $MN$ . Nếu cho $XY$ cắt $(I)$ tại $H$ thì $AH,AD$ đẳng giác góc $A$

 Việc còn lại ta chứng minh $AD,AR$ đẳng giác . Thật vậy , Gọi phân giác ngoài tam giác $ABC $ là $AK$ thì $K(AIRD)=-1=>A(KIRD)=-1$ nên $AR,AD$ đẳng giác . suy ra $AR$ đy qua $H$ , Vì vậy $XY,AR$ cắt nhau trên $(I)$

=

Mình thì mình học trong quyển này ,

quên mắt mình chưa gọi điểm , $I$ là tâm nội tiếp đó

Gọi $I$ là tâm nội .Bài này điều cần chứng minh đưa về  các đường tròn ngoại tiếp $(AEF),(AIT),(O)$ , cùng đy qua 2 điểm

Thật vậy ,  theo tính chất đường tron $Mix$ thì $DA,DI$ đẳng giác $EDF$ nên $(ITD)$ tiếp xúc với $(DFE),(O)$ .  gọi $(AEF)$ cắt (O) tại $X$ , dễ thấy , tiếp tuyến tại $D, AX,EF$ đồng quy tại $G$ do tc tâm dẳng phương  . nên$\overline{GX}.\overline{GA}=GD^2=\overline{GT}.\overline{GI}$ nên $AXTI$ nội tiếp ,nên các tâm $(AEF),(AIT),(O)$ thẳng hàng , vị tự tâm $A$ tỉ số 2 thì $T,K,H$ thẳng hàng

gọi $JM$ cắt $AME$ tại $P$ , $JN$ cắt $FAN$ tại $Q$ ,  ta có $\widehat{PJQ}+\widehat{AQJ}+\widehat{APJ}=\widehat{FDB}+\widehat{FDE}+\widehat{EDC}=180^o$ nên $A,P,Q$ thẳng hàng , , dễ nhận thấy $FE, PQ$ song song $BC$ nên  $\widehat{PQJ}=\widehat{FDB}=\widehat{NMA}$ nên $PQMN$ nội tiếp  , suy ra $J$ thuộc trục đẳng phương của $(ANF).(AME)$

Gọi $DB$ cắt $(ABC)$ tại $J$ , theo Menelaus thì $\frac{KD}{KB}=\frac{MD}{MH}=\frac{JD}{JB}=\frac{AD^2}{AB^2}$ nên $AK$ đối trung

Lời giải của em cũng có điểm tương đồng với bạn Nguyen Dinh Hoang :

+) đầu tiên em chứng minh : $(ALDI)$ nội tiếp có tâm $P$

Thật vậy : gọi $X,Y$ là trung điểm cung lớn và nhỏ $BC$ , ta sẽ chứng minh $DL$ đy qua $X$ . TA có : $\Delta AEF \sim \Delta XBC$

và $\frac{FK}{KE}=\frac{BD}{CD}$ nên $\widehat{FAK}= \widehat{BXD}$ suy ra  $L$ thuộc $DX$ suy ra$\widehat{ALD}= \widehat{AYX}=\widehat{DIY}$ suy ra $ALDI$ nội tiếp

Lấy phân giác trong và phân giác ngoài $AZ,AU$ , dễ thấy $T$ là trung điểm $ZU$ và  tâm của $(UAID)$ là trung điểm $UI$  , từ đó suy ra $P$ là tâm $(ALDI)$

+)Tiếp theo ta sẽ chứng minh $LJ$ là trục đẳng phương của $(O)$ và $(N,NL)$

Gọi $LJ$ cắt $(O),(AID)$ tại $Q,G$ , ta đy chứng minh $Q$ thuộc  $(N,NL)$ .dễ thấy $(N,NL)$ là đường tròn đẳng phương của $(M,ML)$ và $(AID)$ nên để chứng minh $Q$ thuộc  $(N,NL)$  thì ta chứng minh $Q$ là trung điểm của $GJ$

Điều đó cũng tương đương với việc chứng minh $Q$ thuộc đường tròn đẳng phương của $(ALJ),(AID)$ , tức là chứng minh $(O)$ là đường tròn đẳng phương của $(ALJ),(AID)$ . điều này đúng do$\overline{YJ}.\overline{YA}=-\overline{YI}.\overline{YA}$ nên  $(O)$ là đường tròn đẳng phương của $(ALJ),(AID)$ ,nên ta có dpcm

  

Mình thấy bài toán trên đường tròn nội tiếp dc thầy mình dạy nhiều lắm nên quen thôi , bài toán thì chắc cũng nhiều

 Ta nhận thấy rằng , đường thẳng qua $B$ vuông góc $CM$ , đường thẳng qua $C$ vuông góc $BN$ ,$DI$ đồng quy tại $H$ là trực tâm tam giác $IBC$ . 

.Một điều nữa là $AD,BE,CF$ đồng quy tại $G$ (CEva) . $HG$ cắt $BC$ tại $P$ . dễ dàng khi chiếu các chùm điều hòa lên $HG$ thì 3 đường đồng quy tại $Q$ sao cho $(PGQH)=-1$

Mình sẽ chứng minh đối trng    

 , Gọi đường tròn qua $A,B$ và tiếp xúc $BC$ tại $B$ cắt $AM$ tại $G$,Gọi đường tròn qua $A,C$ và tiếp xúc $BC$ tại $C$ cắt $AM$ tại $G'$ , khi đó $MG.MA=MB^2=MC^2=MG'.MA$ suy ra $G$ trùng $G'$ ta có $\widehat{GBC}= \widehat{BAM}= \widehat{ABD}$ suy ra $BD,BG$ đẳng giác . tương tự suy ra $CG,CE$ đẳng giác , nên suy ra $AF,AM$ cũng đẳng giác góc $A$ nên $AF$ đối trung

 gọi $G,L$ đối xứng với $P,D$ qua $I$ , khi đó $G$ thuộc $FE$ và $GL$ là tiếp tuyền của $(I)$ ,  , có $AL$ đy qua tiếp điểm $A$-bàng với $BC$ nên $IM$ song song $AL$ ,  xét cực và đối cực $(I)$ thì $AL$ là đường đối cực của $G$ , khi đó $AL$ vuông góc $IG$ , suy ra $IP$ vuông góc $IM$

GỌi $(FEA)$ cắt $(ABD)$ tại $H$ , ta có $\frac{PE}{PD}=\frac{PD}{PF}=\frac{Sin (DAP)}{Sin (BAP)}=const$ mặt khác , lấy $H'$ đối xứng với $H$ qua trung điểm $DF$ , bằng góc ta có thể chúng minh hình $ PFH'D$ đồng dạng với tứ giác $PBHE$ suy ra $\frac{HB}{HD}=\frac{HB}{H'F}=\frac{PB}{PF}=const$ suy ra $H$ là giao của $(Apolo)$ dựng trên đoạn $BD$ với tỉ số $\frac{PB}{PF}=const$ với $(ABD)$ nên $H$ cố định ( đinh up  hình nhưng load mãi mà nó chả lên