Bài 6.

a. Dùng hai kết quả sau:

1. Cho tam giác $ABC$ với $M, N$ thuộc $BC$. Khi đó $(AMN)$ tiếp xúc với $(ABC)$ khi và chỉ khi $\angle MAN$ và $\angle BAC$ có chung phân giác.

2. Cho tam giác $ABC$, phân giác $AD$, $T$ thuộc $BC$. Khi đó $AT=TD$ khi và chỉ khi $AT$ tiếp xúc với $(ABC)$

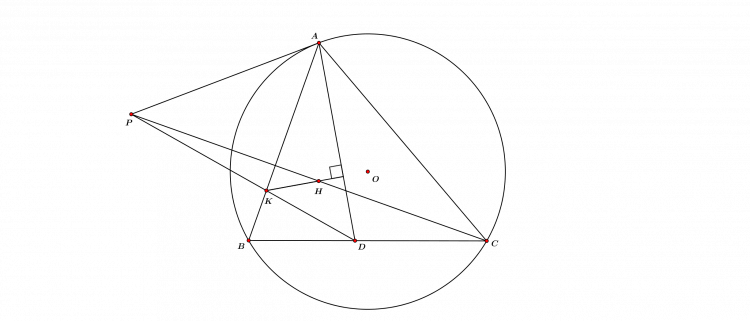
b. Bổ đề. Cho $(O)$ và hai điểm $A, B$ nằm ngoài nó. Qua $A, B$ kẻ các tiếp tuyến $AC, AD, BE, BF$. $CD$ cắt $EF$ tại $G$. Lúc này $OG\perp AB$ tại $H$ thỏa $OG.OH=R^2$

Bổ đề này chứng minh thế nào anh? Nó đã xuất hiện ở những bài toán nào ? Sách nào ?

Bài 4. (China TST 2002) 

Cho tứ giác lồi $ABCD$, gọi $E, F, P$ lần lượt là giao điểm của $AD$ và $BC$, $AB$ và $CD$,  $AC$ và $BD$. Gọi $O$ là chân đường cao hạ từ $P$ xuống $EF$. Chứng minh rằng $\angle AOD=\angle BOC$ 

Bài 3. (9) VMO 2010 

Cho tam giác $ABC$ nội tiếp $(O)$ cố định $B,C$  và $A$ di chuyển trên $(O)$. Gọi phân giác trong và ngoài của tam giác lần lượt là $AD$ và $AE$ với $D,E$ thuộc $BC$. $M$ là trung điểm của $DE$. $H$ là trực tâm của tam giác $ABC$. Chứng minh rằng đường thẳng qua $H$ vuông góc với $AM$ luôn đi qua một điểm cố định khi $A$ di chuyển trên $(O)$.

Bài 2.

Ta có: $MB.MK=ML.MC$ suy ra $M$ thuộc trục đẳng phương của $(CFL)$ và $(KBE)$.

Do đó $MP$ cũng là trục đẳng phương của hai đường tròn này nên $T$ cũng thuộc đường thẳng đó. 

Do đó $TB.TE=TC.TF$ suy ra $T$ thuộc trục đẳng phương của $(ABE)$ và $(ACF)$ nên giao điểm khác $A$ của hai đường tròn nằm trên $AT$.

Chọn đội tuyển KHTN 2013, thầy Hùng có 1 chuyên đề viết về cấu hình này

anh cho em xin tên file

K là điểm gì ?

Câu 6

Mặc dù bài này đã ra lâu rồi nhưng hôm nay em mới bắt tay vào lắm, vì thế em chỉ giải quyết con b) vì con a) quá quen thuộc rồi !

b) Gọi $H$ là giao điểm của $KE\cap BC$, ${V}=KE\cap TU$. Dễ thấy $KE.KH=KP^{2}\Rightarrow \widehat{PHK}=\widehat{KPE}=\widehat{AKP}+\widehat{PAK}$. 

$\widehat{DPK}=\widehat{DTQ}=\widehat{DTF}+\widehat{FTQ}=\widehat{DAF}+\widehat{FQK}=\widehat{DAF}+\widehat{EAF}=\widehat{EAK}$

Suy ra tứ giác $HPDK$ nội tiếp $\Rightarrow \widehat{PKE}=\widehat{PDH}=\widehat{PQT}\Rightarrow KE//QT$

Dễ thấy tứ giác $TULF$ nội tiếp $\Rightarrow \widehat{TUL}=\widehat{AFK}=\widehat{AEK}=\widehat{HPK}\Rightarrow TU//HP$

Mà $(QP,LU)=-1$ $\Rightarrow T(QP,LU)=-1$, Do $EK//TQ$ $\Rightarrow J$ là trung điểm của $VH$ với $J$ là giao điểm của $KE$ và $TP$. Từ đó tứ giác $TVPH$ là hình bình hành suy ra $EK$ đi qua trung điểm $J$ của $TP$.

Đề thi học sinh giỏi lớp 12 TP Hà Nội 

Ngày 30/09/2017

Bài 1. (4 điểm) Cho $x, y, z$ là các số hữu tỉ sao cho $x+y^{2}+z^{2}$, $y+z^{2}+x^{2}$ và $z+x^{2}+y^{2}$ đều là các số nguyên. Chứng minh rằng $2x$ là số nguyên.

Bài 2. (4 điểm) Cho hàm số $f:R\rightarrow R$ thỏa mãn điều kiện 

$f(tanx)=\frac{1}{2}sin2x-cos2x$       $\forall x\epsilon (-\frac{\pi }{2},\frac{\pi }{2})$

Tìm giá trị lớn nhất là nhỏ nhất của biểu thức  $f(sin^{2}x).f(cos^{2}x)$ $(\forall x\epsilon R)$

Bài 3. (4 điểm) Cho tam giác $ABC$ vuông tại $A$ với $AB< AC$. Gọi $M$ là trung điểm của cạnh $AB$, $N$ là điểm nằm trên cạnh $BC$ sao cho $BN=BA$. Đường tròn đường kính $AB$ cắt $(ANC)$ tại $P$. Gọi $E$ là giao điểm của đường thẳng qua $B$ vuông góc với  $MP$ và đường thẳng $AP$, $F$ là giao điểm của đường thẳng qua $B$ song song với $MP$ cắt $PN$ tại $F$. Chứng minh rằng $PC$ chia đôi $EF$.

Bài 4. (4 điểm) Tìm tất cả các đa thức $P(x)$ với hệ số thực sao cho: 

$(P(x))^{2}=2P(x^{2}-3)+1$   $(\forall x\epsilon R)$

Bài 5. (4 điểm) Với mọi $n\epsilon \left \{ 1,2,3 \right \}$ , ta gọi số tự nhiên $k$ là một số tự nhiên kiểu $n$ nếu $k=0$ hoặc $k$ là một số hạng của dãy $1;n+2;(n+2)^{2};(n+2)^{3};...$ hoặc $k$ là tổng của một số số hạng của dãy trên. Chứng minh rằng bất kì số nguyên dương nào cũng biểu diễn được dưới dạng tổng của một số kiểu 1 với một số kiểu 2 và một số kiểu 3.

Bài hình sử dụng hoàn toàn kiến thức lớp 9 và nó là 1 bài toán quen thuộc của lớp 9!

Bài toán. Cho tam giác $ABC$ có tâm đường tròn nội tiếp $I$. Gọi $T$ là giao điểm của $AI$ và $BC$. Gọi $D,E,F$ lần lượt là các điểm tiếp xúc của $BC, CA,AB$ với $I.$ AD cắt (AI) tại G. Đường tròn ngoại tiếp tam giác $ABG$ cắt $AI$ tại $Q$. Chứng minh rằng $B,F,Q,T$ đồng viên.

Bài 3.

Đoạn đầu có thể xử lý được bằng trực đẳng phương như sau:

Gọi $W,G$ lần lượt là trung điểm của $BC$, cung $BC$ chứa $A$.

Xét ba đường tròn $(DM)$, $(\varpi )$, $(ADWG)$ thì ta có trục đẳng phương của ba đường tròn đồng quy tại $S$

Do đó dễ chứng minh $SA$ là phân giác ngoài của tam giác ABC tại đỉnh A.

Còn đoạn sau mình xử lý giống bạn dogsteven.

sao mình thây trong quyển tài liệu chuyên toán ko có nhỉ 

Muôn nơi.

Bạn có thể cho mình hỏi định lí này trong tài liệu nào được không?

Mình có định lý sau: Xét hai chùm $x,y,z,t$ và $x', y', z', t'$ thỏa mãn $x\perp x', y\perp y', z\perp z'$. Khi đó $(xy, zt)=(x'y', z't')\Leftrightarrow t\perp t'$

Ở trên có $O(AD, PM)=A(SP, QA')$, có $OA\perp AS, OD\perp AP, OM\perp AA'$ nên $AP\perp AQ$

 

Dựng $A'$ thuộc $SP$ sao cho $AA' || BC$, khi đó $O(AD, PM)=(AD, PM)=(A'Q, PS)=A(SP, QA')\Rightarrow OP\perp AQ$

Cho mình hỏi tại sao hai chùm điều hòa bằng nhau lại vuông góc

Bài 198. Cho tam giác $ABC$ nội tiếp đường tròn $(O),H$ là trực tâm của tam giác. Tiếp tuyến tại $A$ của đường tròn cắt $CH$ tại $P,$ kẻ phân giác $AD,PD$ cắt $AB$ tại $K.$ Chứng minh rằng $HK$ vuông góc với $AD.$

Mọi người chú ý là lời giải hạn chế tối đa sử dụng phương pháp khác, tập trung vấn đề chủ yếu cho topic ! 

Anh chỉ đề nghị đề cho thầy, tác giả là một bạn người TQ.

 

 

Không ai full hết, có một bạn gần full thôi (sai ý ở câu PTH).

anh còn phầm mềm Maple SOS của anh không ạ em kiếm link nhưng bị die rồi 

Câu bất đẳng thức khối 11 là do một bạn người bạn người Trung Quốc nhờ mình đề nghị.

Bài này là của anh ?

Thêm vài bài giữ lửa  

Bài 16. Cho $x,y,z$ là các số thực không âm thỏa mãn $x+y+z=1$. Chứng minh rằng:

$\frac{z-xy}{x^{2}+xy+y^{2}}+\frac{y-zx}{x^{2}+xz+z^{2}}+\frac{x-yz}{y^{2}+yz+z^{2}}\geq 2$

(Phạm Văn Thuận)

Bài 17. Cho $x,y,z$ là các số thực dương thỏa mãn $x+y+z=xyz+2$. Chứng minh rằng:

$(1-xy)(1-yz)(1-zx)\geq 0$

(Vasile Cirtoaje)

Anh có thể tiếp tục topic được không ạ em khá thích chủ đề này nhưng gần đây topic này không hoạt động 

Cảm ơn em đã ủng hộ topic của anh, từ giờ anh sẽ tập trung cho topic hơn ! Nếu rảnh em hãy rủ bạn bạn của mình vào giữ lửa cho topic

Trước đây bài đề này đã từng được thảo luận ở topic: https://diendantoanh...-3/#entry363791

 

 

Ngoài ra

\[\sum \dfrac{a+3}{(a+1)^{2}} - 3 = \frac12\sum \frac{(abc^2+3)(a-b)^2+ab(a+b+2)(c-1)^2}{(a+1)^2(b+1)^2(c+1)^2} \geqslant 0.\]

Anh Huyện còn link tải phần mềm Maple của anh  không ? Nếu có thì cho em xin link với, em vào blog cũ của anh link hỏng hết rồi!

Cho mình hỏi topic này cho lớp 10 hay cả 11 và 12?

1 cách nữa

Nhìn vào đề bài như thế này ta thường hay nghĩ đến cách đổi biến

Với ý tưởng đó, ta đặt $\frac{x}{y}=a, \frac{y}{z}=b, \frac{z}{x}=c$ thì $abc=1$

$$T=\frac{1}{(a^4+1)(b+c)^3}+\frac{1}{(b^4+1)(c+a)^3}+\frac{1}{(c^4+1)(a+b)^3}$$

Áp dụng BĐT AM-GM:

$$(b+c)^3\geq 8bc\sqrt{bc}=\frac{8}{a\sqrt{a}}\geq \frac{16}{a^2+a}$$

Suy ra

$$16T\leq \frac{a^2+a}{a^4+1}+\frac{b^2+b}{b^4+1}+\frac{c^2+c}{c^4+1}$$

Ta có 

$$\frac{a^2+a}{a^4+1}\leq \frac{3(a^2+a)}{2(a^2+a+1)}\Leftrightarrow (a-1)^2(a+1)(3a^2+4a+3)\geq 0$$ (đúng)

Suy ra 

$$\frac{a^2+a}{a^4+1}+\frac{b^2+b}{b^4+1}+\frac{c^2+c}{c^4+1}\leq \frac{3}{2}\sum \frac{a+1}{a^2+a+1}\leq 3$$

(BĐT quen thuộc:nếu $abc=1$ thì $\sum \frac{a+1}{a^2+a+1}\leq 2$)

Suy ra $T\leq \frac{3}{16}$

1 cách nữa

Nhìn vào đề bài như thế này ta thường hay nghĩ đến cách đổi biến

Với ý tưởng đó, ta đặt $\frac{x}{y}=a, \frac{y}{z}=b, \frac{z}{x}=c$ thì $abc=1$

$$T=\frac{1}{(a^4+1)(b+c)^3}+\frac{1}{(b^4+1)(c+a)^3}+\frac{1}{(c^4+1)(a+b)^3}$$

Áp dụng BĐT AM-GM:

$$(b+c)^3\geq 8bc\sqrt{bc}=\frac{8}{a\sqrt{a}}\geq \frac{16}{a^2+a}$$

Suy ra

$$16T\leq \frac{a^2+a}{a^4+1}+\frac{b^2+b}{b^4+1}+\frac{c^2+c}{c^4+1}$$

Ta có 

$$\frac{a^2+a}{a^4+1}\leq \frac{3(a^2+a)}{2(a^2+a+1)}\Leftrightarrow (a-1)^2(a+1)(3a^2+4a+3)\geq 0$$ (đúng)

Suy ra 

$$\frac{a^2+a}{a^4+1}+\frac{b^2+b}{b^4+1}+\frac{c^2+c}{c^4+1}\leq \frac{3}{2}\sum \frac{a+1}{a^2+a+1}\leq 3$$

(BĐT quen thuộc:nếu $abc=1$ thì $\sum \frac{a+1}{a^2+a+1}\leq 2$)

Suy ra $T\leq \frac{3}{16}$

cho e hỏi làm sao lại tìm ra được BĐT đó (MÀU ĐỎ )

Lời giải bài 14: 

Trước tiên xin chứng minh BĐT quen thuộc: $a^2+b^2+c^2+2abc+1\geq 2(ab+bc+ca)$ theo kiểu dồn biến.

Giả sử $c$ bé nhất trong $3$ số.

Đặt: $f(a,b,c)=a^2+b^2+c^2+2abc+1-2(ab+bc+ca)$.

Ta có: 

$f(a,b,c)-f(\sqrt{ab},\sqrt{ab},c)=(\sqrt{a}-\sqrt{b})^2(a+b+2\sqrt{ab}-2c)\geq 0$.

Do đó, ta có: $f(a,b,c)\geq f(\sqrt{ab},\sqrt{ab},c)$.

Ta chứng minh: $f(\sqrt{ab},\sqrt{ab},c)\geq 0$.

Thật vậy: $f(\sqrt{ab},\sqrt{ab},c)=(c-1)^2+2c(\sqrt{ab}-1)^2\geq 0$.

Áp dụng BĐT vừa chứng minh:

$(a^2+b^2+c^2+2abc+1)^2\geq 4(ab+bc+ca)^2\geq 12abc(a+b+c)\geq 36(abc)^2$.

Suy ra: $a^2+b^2+c^2+2abc+1\geq 6abc$.

Từ đó, ta có đpcm.

 

P/S: Bài này là của mình á bạn.

Cảm ơn Bảo đã đưa ra lời giải, mình cũng đa ghi nguồn cho bài toán, hi vọng bảo sẽ góp lửa cho topic nhiều hơn !

   Tiếp tục 

Bài 14. Cho a, b, c là các số thực dương thỏa mãn $\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\geq 3$. Chứng minh rằng:

$a^{2}+b^{2}+c^{2}-4abc+1\geq 0$                                                                   

(Sưu Tầm)

P/s: Bài này bạn Baoriven đã up lên diễn đàn, tạm thời mình chưa biết nguồn nên để là sưu tầm!

Bài 15. Cho x, y, z là các số thực dương thỏa mãn $x+y+z=1$. Chứng minh rằng 

$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+48(xy+yz+zx)\geq 25$