a) Gọi $B'$ đối xứng $B$ qua $CD$, $AB$ cắt $CD$ tại $G$ thì ta có $G$ là tđ $CD$ vậy $BCB'D$ là hbh nên $AE/AC=AB/AB'=AF/AD => EF//CD$

Bài 4: Gọi $E$ là điểm bất kì trên $d$, $AB$ cắt $OH$ tại $C$

$P(C/E)=CH^2=CA.CB=P(C/O)=OC^2-R^2$

Bài 2: CMTT như bài làm của mình ở đây: https://diendantoanh...-năm-2017-2018/

Thay $n=2$ vào dễ thấy $P(x)=1$

Bài 4: $P(2017)=1, P(n)|3^n-1\forall n \in Z^{+}$

Ta xét $2$ TH sau:

$1.$ $deg(P)\geqslant 0$ , khi đó theo định lý $Schur$ sẽ tồn tại vô số ước nguyên tố $p$ của dãy $P(n)$

Giả sử $p$ là một ước nguyên tố bất kì như thế với $p>3$ và $p|P(m)$, ta có: $p|3^m-1$

Theo tính chất quen thuộc của đa thức nguyên thì $P(m+p)\equiv P(m)\equiv 0(modp)$

Từ đây lại có $p|3^{m+p}-1$ mà $p>3$ và do $a^m \equiv b^m(mod p)$ nên theo định lí $Fermat$ nhỏ ta có: $3^{m+p}-1\equiv 3^m(3^p-1)\equiv 2.3^m(mod p)$

Điều này kéo theo $p|2$ điều này rõ ràng vô lí.

$2.$ $deg(P)=0$ hay $P$ là đa thức hằng thế thì $P(x)=d$ hay $P(x)=P(2017)=1$ thử lại rõ ràng thấy đúng từ đó $P(x) \equiv 1$

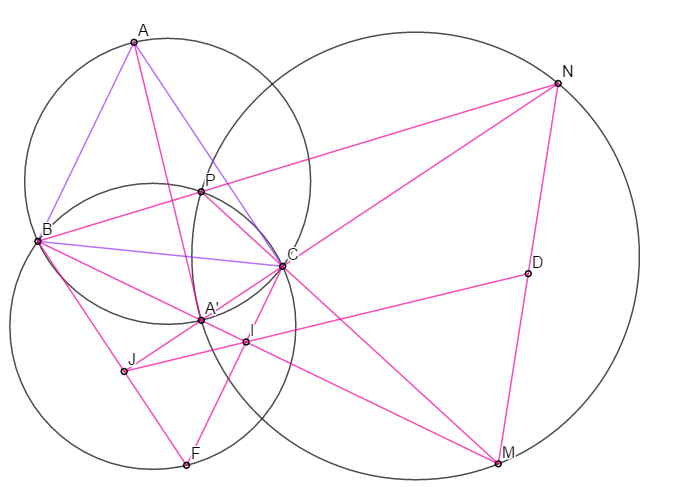
Bài 3: Lời giải rất đơn giản nhưng nghĩ ra được đường cố định thì ...  

Dựng hình bình hành $ABFC$, $BM$, $CN$ cắt $CF$, $BF$ tại $I$, $J$; $A'$ đối xứng $A$ qua $O$

Bài 1: Do vài trò đối xứng giữa 3 biến WLOG ta giả sử $x \geqslant y \geqslant z$

BĐT đã cho tương đương với: $A=\sum \frac{3-xy}{\sqrt{2(3-xy)}}\geqslant 3\Leftrightarrow \sum \frac{6-2xy}{5-xy}\geqslant 3\Leftrightarrow \sum \frac{1-xy}{5-xy}\geq 0$

Áp dụng BĐT Chebyshev ta có $A\geq (3-\sum xy)(\sum \frac{1}{5-xy})\geq 0$ do $\sum xy\leqslant \frac{(\sum x)^2}{3}=3$

Vậy ta có BĐT cần CM, dấu $=$ xảy ra khi và chỉ khi $x=y=z=1$

Để giải bài này trước hết ta cần 2 bổ đề sau:

$1.$ Bổ đề $ERIQ$: https://julielltv.wo.../15/bo-de-eriq/

$2.$ Bổ đề $Cevian Nest$: https://artofproblem...342_cevian_nest

Trở lại bài toán:

Khi đó $B(PHIC)=C(EAQD)=C(HPBI)=C(PHIB) => P,H,I$ thẳng hàng

Bài 6: (Hoàn thiện lời giải bài tổ hợp của anh Supermember )

Ta sẽ xử lí trường hợp $n\geqslant 5$ và $n$ nguyên tố bằng số học, đặt $n=p$

Lại có: $S(A_p)=pa^2+p(p+1)ab+\frac{p(p+1)(2p+1)}{6}b^2$ chia hết cho $p$ (vì $p$ nguyên tố) $(1)$

Xét tập $A_p$ có $p$ phần tử theo mod $p$ sẽ được tập $A'_p=(r_1,r_2,...,r_{p})$ với $0\leqslant r_i\leqslant p-1, 1\leqslant i\leqslant p$ 

Xét các tổng $s_i=r_1+...+r_i$, ta được $p$ tổng như vậy

Chú ý rằng, với mỗi $p$ nguyên tố, ta có đúng $\frac{p+1}{2}$ số chính phương mod $p$

Vì vậy, theo nguyên lí Dirichlet, tồn tại $s_i$, $s_j$, $i<j$ có cùng số dư khi chia cho $p$

Từ đó, lấy $k=s_j-s_i$, dễ dàng thấy $k$ cũng là một tập con của $A$, đồng thời nó chia hết cho $p$ $(2)$

Từ $(1)(2)$, ta có ngay $(S(A_p),k)\geqslant p$ vì vậy không thỏa mãn $S(A_p)$ nguyên tố với mọi tổng tập con của $A_p$

Vậy ta có ĐPCM.

Đổi tên $2$ điểm liên hợp đẳng giác là $P$, $Q$ như hình vẽ.

Gọi $BE, CF, BK, CL$ lần lượt là các đường cao của $QBC$ và $ABC$, $S$ là giao của $FK$ và $EL$

Bằng cộng góc đơn giản dễ có $PC//LE$ và $PB//KF$

Gọi $AP$ cắt $DE$ tại $H$ thì áp dụng định lí $Menelaus$ cho tam giác $APC$ cát tuyến $HGE$ và tam giác $APB$ cát tuyến $HFD$ với chú ý $DE//BC$ thì có ngay $HD/HF=HE/HG$ hay $HD.HG=HE.HF$ tức $P(H/(PGD))=P(H/(PFE))$ vì vậy $A$ thuộc trục đẳng phương nên $AP$ vuông góc $OI$

Kết quả này đã bao gồm trong chứng minh của mình ở đây: https://diendantoanh...-định/?p=714387

Bài toán trên sai hoặc thiếu đề. Nếu cho C,D cố định dễ thấy ngay đề vô lí

Kẻ $AH$ vuông góc $BC$, $DT$ cắt $AB$ tại $G$, đgt | $DT$ cắt $OM$ tại $X$

Theo hàng điều hòa quen thuộc thì $D(AFGB)=D(AFTB)=-1$

Chú ý: $DA|AO, DF|AM, DT|AX, DB|AH$

Do $AH//OM$ nên dễ thấy $A(OXMH)=-1$ hay $X=O'$ đối xứng $O$ qua $M$

Hệ quả: $AT$ cắt $BC$ tại $I$ thì do $(DIBC)=-1$ nên $A,T,S$ thẳng hàng

Gọi $R, r$ là bán kính ngoại, nội tiếp, $H$ là trực tâm, $AI$ cắt $(O)$ tại $U, G$ là giao của $MK$ với $EF$

Áp dụng công thức diện tích $ABC$ ta đc $BC. MG=abc/4R$

Lại có $KE^2=GK^2+GE^2=(R-MG)^2+(R^2-OG^2)=2R^2-2R.MG+MO^2+2MO.OG=2R^2-1/2bc+MO^2+1/4(R^2-OH^2)=MO^2-1/2bc-1/4(a^2+b^2+c^2)=R^2+1/4(b-c)^2=MK^2+MD^2=KD^2$

Từ đó $KE=KF=KD$ hay $K$ là tâm $(EFD)$

Ta có bài toán tổng quát hơn với chú ý: $P(I/DEF)=IK^2-KX^2=r^2-2Rr$ là: $I$ là trục đp của các đg tròn đối xứng như trên

Gọi $AE$ cắt $(O)$ tại $K, G$ đx $F$ qua $K$, $AJ$ cắt $(O)$, $(B,BC)$ tại $I,M, FJ$ cắt $BC$ tại $H, D$ là chân đg cao, $C'$ đx $C$ qua $D$

Ta có: $AF^2=AG^2=AC^2=AD.AB => AFD=AGD(=DBG) => BA.BD=BF.BG=BK.BE => (BEGF)=-1$ (Maclaurin đảo)

CMTT thì $(AEMJ)=-1$

Bài 1: Kéo dài XB cắt YC tại J dễ thấy J thuộc (I)

Gọi F là tđ BC, G là tđ AH thì theo kq quen thuộc AH=2OF nên AG=GH=OF nên GF//AE. Chú ý DI là trung tuyến ADE nên theo bổ đề hình thang thì DI đi qua tđ J của GF và cũng là tđ OH. Chú ý DP//HO nên theo tỉ số đơn thì D(HOJP)=(HOJ)=-1. Gọi OD giao AB, AC tại X,Y thì D(AXNQ)=D(AYPM)=-1 nên (AXNQ)=(AYMP) từ đó MN, PQ, XY đồng quy hay nói cách khác K,O,D thẳng hàng

a) Gọi tâm (AEF) là O'

Bài 1 của em ạ:

 Bổ đề Cho tam giác $ABC$, tiếp tuyến tại $A, C$ cắt nhau tại $E$. Khi đó: $sinAEB/sinCEB=(AC/BC)^2$

$sinAEB/sinCEB=sinAEB/sinBAE.sinBAE/sinBCE.sinBCE/sinBEC=AB/BE.sinBCA/sinBAC.BE/AC=(AB/AC)^2$

Áp dụng định lí $Ceva$ sin cho 3 đường $BAb, CAc, AA1$ đồng quy tại $A1$