Mình vừa mới nghĩ ra lời giải bài toán mới của thầy Hùng http://analgeomatica.blogspot.com/ Tuần 2 tháng 3 nên đăng trước khi đi ngủ, với lại mình vừa đăng bài lần đầu nên chưa hiểu rõ cách đăng bài, xóa post,.. ra sao, mong mọi người thông cảm  . Xin trích dẫn bài toán mới của thầy Hùng thay bạn Zaraki 

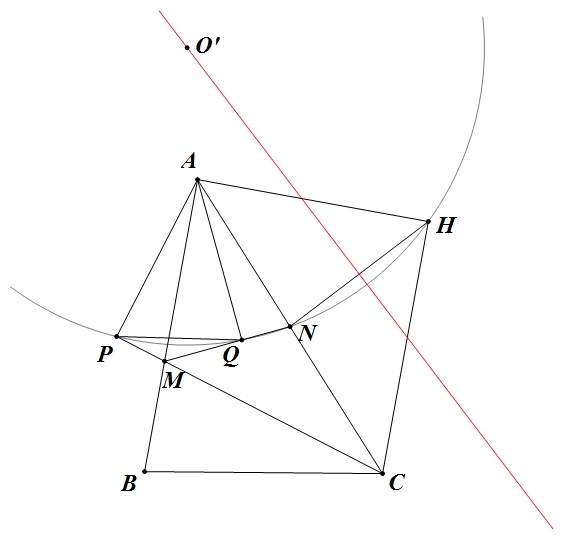
 Bài 28: Cho tam giác $ABC$ với các điểm $E, F$ thuộc $CA, AB$ sao cho $B, C, E, F$ cùng thuộc đường tròn. Gọi $M, N$ là trung điểm của $BE, CF$. $MN$ cắt $Ca, AB$ tại $K, L$. $P$ là trung điểm $KL$. $BE$ giao $CF$ tại $H$. Chứng minh $\angle HAB = \angle PAC$.

              Lời giải của mình:

• Gọi $S = LK \cap EF$, sử dụng Menelaus ta có $\dfrac{\overline{LB}}{\overline{LF}} = - \dfrac{\overline{LB}}{\overline{LF}}.\dfrac{\overline{ME}}{\overline{MB}} = - \dfrac{\overline{SE}}{\overline{SF}} = - \dfrac{\overline{NC}}{\overline{NF}}.\dfrac{\overline{KE}}{\overline{KC}} = \dfrac{\overline{KE}}{\overline{KC}}$ ($M, N$ là trung điểm $EB, FC$). Do đó nếu ${X; H} = (BHF) \cap (CHE)$ thì $X$ là tâm vị tự quay biến $B \mapsto E, F \mapsto C$, suy ra $L \mapsto K$. Do đó, $X$ cũng là tâm vị tự quay biến $BE \mapsto LK, M \mapsto P$, do đó $\triangle XBL \sim \triangle XMP \sim \triangle XEK$, tương tự $\triangle XLF \sim \triangle XPN \sim \triangle XKC$, từ đó ta có $\dfrac{\overline{LB}}{\overline{LF}} = \dfrac{\overline{PM}}{\overline{PN}} = \dfrac{\overline{KE}}{\overline{KC}} (1)$
•  
• Gọi $Y = BP \cap FC, Z = CP \cap EB$, lại sử dụng Menelaus lần nữa ta có $\dfrac{\overline{YN}}{\overline{YF}} = \dfrac{\overline{BL}}{\overline{BF}}.\dfrac{\overline{PN}}{\overline{PL}} = \dfrac{\overline{EK}}{\overline{EC}}.\dfrac{\overline{PN}}{-\overline{PK}} = \dfrac{\overline{PM}}{-\overline{PK}}.\dfrac{\overline{CK}}{\overline{EC}}$ (do (1)) $= \dfrac{\overline{PM}}{\overline{PK}}.\dfrac{\overline{CK}}{\overline{CE}} = \dfrac{\overline{ZM}}{\overline{ZE}}$, do $M, N$ lần lượt là trung điểm $EB, FC$ nên $\dfrac{\overline{YF}}{\overline{YC}} = \dfrac{\overline{ZE}}{\overline{ZB}}$.
•  
• Từ $B$ kẻ đường thẳng song song $FC$ cắt $AC$ tại $U$, từ $C$ kẻ đường thẳng song song $EB$ cắt $AB$ tại $V$, $T = BU \cap CV$, ta có $ B(ACPT)$ $=$ $B(FCYT)$ = $\dfrac{\overline{YF}}{\overline{YC}}$ = $\dfrac{\overline{ZE}}{\overline{ZB}}$ =$ C(EBZT)$ $=$ $C(ABPT)$, do đó $\overline{A, P, T}$ do dễ thấy $A, B, C, P, T$ không cùng thuộc đường tròn. Công việc còn lại của chúng ta chỉ là chứng minh $AH, AT$ đẳng giác trong góc $\widehat{BAC}$
• Bổ đề: Cho $\triangle ABC$, một đường tròn $(O)$ đi qua $B, C$ cắt $AB, AC$ lần lượt tại $Y, X$. Gọi $P = BX \cap CY$. Kẻ hình bình hành $BPCQ$. Khi đó $AP, AQ$ đẳng giác trong góc $\widehat{BAC}$. Bổ đề này quen thuộc, xin phép không chứng minh ở đây ạ

Lời giải của mình :
Trung trực $ID$ cắt $IB, IC$ tại $N,S$. Ta có $FI = FB$ nên $FN \perp BI$. Tương tự $ES \perp IC$. Do đó $F, N, S, E$ đồng viên. Do $M$ là trung điểm $EF$ nên $MF = MN$, ta có $MQ \perp FN$ nên $MQ$ là trung trực $FN$, suy ra $\triangle QFN$ cân tại $Q$. Do $\widehat{QNF} = 90° - \dfrac{\widehat{ABC}}{2}$ nên $\widehat{FQN} = \widehat {ABC}$, do $ QR//BC$ nên $FQ//AB$. Do $F$ là điểm chính giữa của cung $AB$ không chứa điểm $C$ nên $QF$ là tiếp tuyến của $(O)$. Tương tự $RE$ là tiếp tuyến của $(O)$. Gọi $K = FQ \cap RE$. Ta dễ dàng suy ra $M$ là tâm nội tiếp $\triangle KQR$. Do $KQ, KR$ tiếp xúc $(O)$ tại $F, E$ và $M$ là trung điểm $EF$ nên đường tròn $(O)$ là đường tròn mixtilinear trong góc $\widehat{QKR}$ của $(KQR)$. Ta lại có $\triangle KQR$ và $\triangle ABC$ có các cạnh tương ứng sông song nên $QB, KA, RC$ đồng quy tại $X$ là tiếp điểm của $(O)$ và $(KQR)$. Do $I, M$ là tâm nội tiếp $\triangle ABC, \triangle KQR$ nên $\overline{X, I, M}$. Khi đó $IM$ cắt $(KQR)$ tại $P'$ thì $P'$ thuộc trung trực $QR$, do đó $P'$ trùng $P$ hay $P \in (KQR)$. Ta có đpcm.

Lời giải: 

Ta có $A, E, P, B$ đồng viên và $AP$ là phân giác $\widehat{BAE}$ nên $PE = PB$, tương tự $PC = PF$, mặt khác $\widehat{BPE} = 180^{\circ} - \widehat{BAC} = \widehat{CPF}$, nên $\widehat{BPF} = \widehat{CPE}$, do đó $\triangle BPF = \triangle EPC$, ta suy ra $BF = CE$. Do $R$ là tâm vị tự quay biến $FE \mapsto BC$ nên $R$ là điểm chính giữa của các cung $BAC, EAF$ hay $AR$ là phân giác ngoài của $\triangle ABC$. 

Sử dụng định lí Ce-va dạng lượng giác cho $\triangle ABC$ với $AL, BL, CL$; $AK, BK, CK$ và $AP, BP, CP$ đồng quy:

 $\dfrac{\sin{\widehat{LAB}}}{\sin{\widehat{LAC}}}. \dfrac{\sin{\widehat{LCA}}}{\sin{\widehat{LCB}}}.\dfrac{\sin{\widehat{LBC}}}{\sin{\widehat{LBA}}} = 1$; $\dfrac{\sin{\widehat{KAB}}}{\sin{\widehat{KAC}}}. \dfrac{\sin{\widehat{KCA}}}{\sin{\widehat{KCB}}}.\dfrac{\sin{\widehat{KBC}}}{\sin{\widehat{KBA}}} = 1$; $\dfrac{\sin{\widehat{PCB}}}{\sin{\widehat{PCA}}}. \dfrac{\sin{\widehat{PAC}}}{\sin{\widehat{PAB}}}.\dfrac{\sin{\widehat{PBA}}}{\sin{\widehat{PBC}}} = 1$. Nhân theo vế, rút gọn và chú ý $\widehat{LAB} = \widehat{KAC}$, $\widehat{LAC} = \widehat{KAB}$, $\widehat{PAB} = \widehat{PAC}$, ta có:

$\dfrac{\sin{\widehat{LBC}}}{\sin{\widehat{LBA}}}. \dfrac{\sin{\widehat{KCA}}}{\sin{\widehat{KCB}}} = 1$. hay là $\dfrac{\sin{\widehat{JBC}}}{\sin{\widehat{JBA}}}. \dfrac{\sin{\widehat{JCA}}}{\sin{\widehat{JCB}}}.\dfrac{\sin{\widehat{PAB}}}{\sin{\widehat{PAC}}} = 1$ hay $\overline{A, P, J}$.

Gọi $X$ là tâm $(AEF)$. $BP, CP$ thứ tự cắt $(PAC), (PAB)$ tại điểm thứ hai $Z, Y$. Ta có $B, C, Y, Z$ đồng viên. Ta có:

$BX^2 - CX^2 = \mathcal{P}_{B/(X)} - \mathcal{P}_{C/(X)} = \overline{BF}.\overline{BA} - \overline{CE}.\overline{CA} = \overline{BP}.\overline{BZ} - \overline{CP}.\overline{CY} = \overline{BP}(\overline{BP}+\overline{PZ}) - \overline{CP}(\overline{CP}+\overline{PY}) = PB^2 - PC^2$. Suy ra $PX \perp BC$, từ đó $\overline{P, N, X}$. 

Ta có $T$ đối xứng $A$ qua $NX$, $S$ đối xứng $A$ qua $NJ$ $\Rightarrow$ $\widehat{PNJ} = \dfrac{1}{2}.\widehat{TNS} = \widehat{TNM}$, hay là $\widehat{ONM} = \widehat{PNT} = \widehat{PNA}$. Do đó $NA, NM$ đẳng giác trong góc $\widehat{PNJ}$. Gọi $l$ là đường thẳng đẳng giác với $ND$ trong góc $\widehat{PNJ}$. Ta có: $(NM, l, NO, NP) = (NA, ND, NP, NJ) = (ADPJ) = -1 = (ST, AM, AS, AT)$, do $NM \perp ST, NO \perp AS, NP \perp AT$ nên $l \perp AM$, do đó $\widehat{MAS} = (l, NO) = \widehat{PND} = \widehat{NDC} - 90^{\circ}$. 

Chắc lời giải trên cũng giống bạn Bảo thôi, nhưng mình viết chi tiết hơn

Trong lời giải của em có chứng minh $PX$ vuông góc $AT$ với $X$ là tâm $(AEF)$

Thưa thầy, thầy có ý tưởng gì về bài toán tổng quát không ạ, em vẽ hình mãi không ra

Mình chưa hiểu tại sao bạn Bảo chứng minh được $\triangle KNA \sim \triangle LMA$, mới chỉ có một cặp cạnh tỉ lệ thôi.

Tổng kết lại một chút, ta có thể viết lại bài toán này như sau

 

Cho tam giác $ABC$ và một đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$ khác $C,B$. $BE$ cắt $CF$ tại $H$. Một đường thẳng qua $H$ cắt $CA,AB$ tại $M,N$. Trên $BC$ lấy $P,Q$ sao cho $MP\parallel BE$ và $NQ\parallel CF$. $MP$ cắt $NQ$ tại $R$. Chứng minh rằng $(PQR)$ tiếp xúc $(ABC)$.

 

Figure3780.png

 

Thực sự rằng kết quả này thì lại không mới, mình đã lần đầu tổng quát kết quả này từ kết quả của anh Đào Thanh Oai tại đây từ khoảng 2,3 năm trước http://oaithanhdao.b...tangent-to.html, tuy nhiên mình chỉ dùng nó tập huấn đội tuyển KHTN chứ chưa công bố ở đâu. 

 

Trước đây mình nhớ cũng có một bạn nào post một kết quả tương tự thế này lên ddth nhưng mình không tìm lại được link.

 

Gần đây kết quả này được xuất hiện dưới dạng bổ đề bởi bạn Lê Viết Ân ở đây http://artofproblems...c6t48f6h1236077

 

Đến thời điểm này thì việc ai tìm ra và có trước sau thế nào không mấy quan trọng nữa, quan trọng là chúng ra đang từng bước tìm ra những lời giải khác đẹp cho bài toán trên. Hy vọng các bạn hãy cùng tham gia giải quyết tiếp bài toán trên.

Một cách giải khác cho bài toán trên :

$MP, NQ$ thứ tự cắt $AB, AC$ tại $X, Y$. Do $B, C, E, F$ đồng viên nên $M, N, X, Y$ đồng viên và ta có $\dfrac{BX}{BN} = \dfrac{HM}{HN} = \dfrac{CM}{CY}$. (1) 

$(XNR)$ cắt $(YMR)$ tại điểm thứ hai $S$. Vì $S$ là tâm vị tự quay biến $XN \mapsto MY$ và cũng do (1) nên biến $B \mapsto C$. Do $S$ là điểm Miquel của tứ giác toàn phần $AMNRYX$ nên $S \in (AMX)$. Mặt khác phép vị tự quay tâm $S$ biến $XM \mapsto BC$ nên $S \in (ABC)$.

Ta lại có $\triangle SXM \sim \triangle SBC$ nên $S, X, B, P$ đồng viên, tương tự $S \in (CQY)$. Do đó $\widehat{SPQ} = \widehat{SXN} = \widehat{SRQ}$ nên $S \in (PQR)$, và ta có $\widehat{BSP} = \widehat{BXP} = \widehat{CYQ} = \widehat{CSQ}$. 

Kẻ tiếp tuyến $Sx$ của $(ABC)$, ta có $\widehat{PQS} = \widehat{BCS} + \widehat{CSQ} = \widehat{BSx} + \widehat{BSP} = \widehat{PSx}$, do đó $Sx$ là tiếp tuyến của $(PQRS)$, từ đó ta có đpcm.

Bài 33 (Saudi Arabia TST). Cho ba số thực dương $a,b,c$ thỏa mãn điều kiện $a+b+c=3.$ Chứng minh rằng \[\frac{1}{a^2+b^2+c^2}+\frac{1}{\sqrt{abc}} \geqslant \frac{4}{3}.\]

.
Đặt $t=ab+bc+ca$, với $t \in (0;3]$.
Sử dụng liên tiếp AM-GM ta có $3^6 = [a^2+b^2+c^2+2(ab+bc+ca)]^3 \geq 27(a^2+b^2+c^2)(ab+bc+ca)^2$ $\Leftrightarrow$ $\frac{1}{a^2+b^2+c^2} \geq \frac{t^2}{27}$. Mặt khác $3 \geq t \geq 3 \sqrt[3]{a^2b^2c^2}$. Do đó $\frac{1}{\sqrt{abc}} \geq \sqrt{\dfrac{27}{t^3}}$. Từ đó ta có $\frac{1}{a^2+b^2+c^2} + \frac{1}{\sqrt{abc}} \geq \frac{t^2}{27} + \sqrt{\frac{27}{t^3}} = \frac{t^2}{81}.3 + \frac{1}{9}\sqrt{\frac{27}{t^3}}.4 + \dfrac{5}{9}\sqrt{\frac{27}{t^3}} \geq 7\sqrt[7]{(\frac{t^2}{81})^3.(\dfrac{1}{9}\sqrt{\frac{27}{t^3}})^4} + \frac{5}{9} = \frac{4}{3}$. Dấu bằng xảy ra khi $a=b=c=1$.

Lời giải:
Gọi $O, I$ là tâm ngoại tiếp tam giác $\triangle ABC, \triangle DEF$. Do $\triangle ABC$ và $\triangle DEF$ có các cạnh tương ứng song song nên $AD, BE, CF$ đồng quy tại tâm vị tự $H$. Khi đó ta cũng có $I, H, O$ thẳng hàng. Đường thẳng qua $D, E, F$ song song $PA, PB, PC$ đồng quy tại $L$ và ta có $P, H, L$ thẳng hàng. Gọi $k = \frac{HD}{HA}$, ta có $k$ cố định. Do đó $\frac{DL}{DQ} = \frac{EL}{EQ} = \frac{FL}{FQ} = k$. Từ đó ta suy ra $D, E, F$ thuộc đường tròn Apollonius ứng với tỉ số $k$ của đoạn thẳng $LQ$. Ta có ngay $I \in LQ$. Khi đó $ID$ là tiếp tuyến của $(DLQ)$ nên nếu gọi $R$ là bán kính $(DEF)$ thì $\frac{ID}{IQ} = \frac{DL}{DQ} = k$, do đó $Q \in (I; \frac{R}{k})$. Suy ra $IL = \frac{ID^2}{IQ} =kR$. Từ đó ta tính được $OP = IL.\frac{OH}{HI} =k^2R$ hay $P \in (O;k^2R)$. Mặt khác dễ thấy tiếp tuyến tại $Q$ của $(I; \frac{R}{k})$, tiếp tuyến tại $L$ của $(I; kR)$ và tiếp tuyến tại $P$ của $(O;k^2R)$ song song nên PQ đi qua tâm vị tự $K$ của $(I; \frac{R}{k})$ và $(O; k^2R)$, hay $PQ$ đi qua điểm đối xứng với $H$ qua trung điểm $OI$.

Theo em nghĩ, khó có thể thay thế hai tam giác có cạnh tương ứng song song, có thể thay trọng số bất kì cho hệ thức đoạn thẳng bằng nhau, nó không ảnh hưởng gì cả

Em nghĩ để theo hệ thức $PA:PB:PC=QD:QE:QF$ thì lời giải của em nó không bị ảnh hưởng gì mà, chỉ khác một chút về đường tròn Apollonius thôi ạ.

Mình xin mở màn bài đầu tiên
$\boxed{\text{Lời giải bài toán 1:}}$
Gọi $H$ là trực tâm $\triangle ABC$. Ta dễ dàng tính được $\widehat{BHC} = \widehat{BIC} = \widehat{BOC} = 120^{\circ}$. Do đó $B, H, I, O, C$ đồng viên. Nếu gọi $J$ là tâm $(BIC)$ thì $J$ đối xứng với $O$ qua $BC$. Ta có $\widehat{OIX} = 90^{\circ}-\frac{\widehat{AJO}}{2} = 90^{\circ}-\frac{\widehat{BJO}-\widehat{AJB}}{2} = 90^{\circ}-\frac{90^{\circ}-\frac{\widehat{BOJ}}{2}-\widehat{ACB}}{2}= 80^{\circ} = \widehat{AXO}$. Do đó $OI=OX$. Ta có $\widehat{BXJ} = 80^{\circ} =\widehat{ABC} = \widehat{CEJ} = \widehat{BEJ}$ nên $B, E, X, J$ đồng viên. Do $\triangle BOJ$ đều nên $\triangle XOE$ đều, do đó $OX=OE$. Do $\widehat{OEK}=\widehat{OKE}=80^{\circ}$ nên $OK=OE$.
$(J;JC)$ cắt $AC$ tại điểm thứ hai $L'$. Ta có $OI=OL'$ và $\widehat{MOL'}=\widehat{BOL'}-\widehat{BOM}=140^{\circ}-40^{\circ}=100^{\circ}$(do ta dễ dàng tính được $\widehat{AMO}=40^{\circ}$). Suy ra $\widehat{OKL'}=40^{\circ}=\widehat{ACB}$ nên $K,M,C,L'$ đồng viên. Từ đó ta suy ra $\widehat{CL'E}=180^{\circ}-\widehat{AL'O}-\widehat{OL'E}=180^{\circ}-\widehat{OBC}-50^{\circ}=100^{\circ}=\widehat{CKM}=\widehat{CL'M}$(do $L' \in (O;OK)$), do đó $L' \in ME$ nên $L' \equiv L$. Hay là $L \in (O;OI)$. Từ đó ta tính được $\widehat{CEL}=40^{\circ}=\widehat{KFC}$ nên $K, E, L, F$ đông viên hay $OF=OK$. Từ đó ta có đpcm.
Chú thích: Ta có thể chứng minh bài sau: Chứng minh rằng $(F;FK)$ tiếp xúc $(O)$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline \end{array}$$

Lời giải bài 9.
Ta có $\sum_{cyc}\sqrt{\dfrac{a+b}{2c}} \geq \sum_{cyc}\dfrac{\sqrt{a}+\sqrt{b}}{2\sqrt{c}} \geq \dfrac{1}{2}\sum_{cyc}\sqrt{a}\left (\frac{1}{\sqrt{b}}+\dfrac{1}{\sqrt{c}}\right ) \geq \sum_{cyc}\dfrac{2\sqrt{a}}{\sqrt{b}+\sqrt{c}} \geq \sum_{cyc}\sqrt{\dfrac{2a}{b+c}}$.

 

Bài toán 10. Cho $a, b, c >0$. Chứng minh rằng:
\[(a+b+c)\left(\dfrac{a}{b^2+c^2} + \dfrac{b}{c^2+a^2} + \dfrac{c}{a^2+b^2}\right) \geq 4+ \dfrac{4a^2b^2c^2}{(a^2+b^2)(b^2+c^2)(c^2+a^2)}\]

 

 \begin{array}{| l | l |} \hline \text{HDTterence2k} & 1\\ \hline \text{hoanglong2k} & 3\\ \hline \text{Gachdptrai12} & 4\\ \hline \text{Nguyenhuyen_AG} & 3\\ \hline \text{fatcat12345} & 1\\ \hline \text{lenhatsinh3} & 1\\ \hline \text{tuanyeubeo2000} & 1\\ \hline \text{Ngockhanh99k48} & 1 \\ \hline \end{array} 

 Một lời giải khác cho bài toán 14:
 Đặt $\frac{a+b}{2}=z, \frac{b+c}{2}=x, \frac{a+c}{2}=y$.

 Ta có $x+y+z=1$, sử dụng AM-GM ta có $\frac{a+b}{ab+1} \geq \frac{a+b}{(\frac{a+b}{2})^2+1}=\frac{2z}{z^2+1}$.

 Phần còn lại ta chứng minh $\frac{x}{x^2+1} +\frac{y}{y^2+1} +\frac{z}{z^2+1} \geq \frac{9}{10}$.

 Đó là BĐT Polish 96 nổi tiếng.

$\boxed{\text{Lời giải bài toán 18:}}$
Đường thẳng qua $C$ song song $AB$ cắt đường thẳng qua $A$ vuông góc $AB$ tại $H$. Ta có $\triangle AHC$ vuông tại $H$ nên $\triangle NHC$ cân tại $N$. Do đó $\widehat{NHP}=\widehat{NHC}-\widehat{PHC}=\widehat{NCH}-\widehat{PAC}$(do $P, A, H, C$ đồng viên) $= \widehat{BAC}-\widehat {PAC}=\widehat{BAP}=\widehat{MQP}$. Do đó $(PQN)$ đi qua điểm $H$ cố định hay tâm $(PQN)$ thuộc trung trực $NH$ cố định. Ta có đpcm.

P/s: mãi mới tranh bài để được giải, các bạn giải nhanh quá . Mình xin đề xuất bài toán 19 sau, mình sưu tầm được từ thầy Nguyễn Minh Hà
$\boxed{\text{Bài toán 19: }}$ Cho tam giác $\triangle ABC$ nội tiếp $(O)$, ngoại tiếp $(I)$. Các điểm $A_b, A_c$ thứ tự thuộc các cạnh $AB, AC$ sao cho $A_bA_c$ song song $BC$ và $A_bA_c$ tiếp xúc $(I)$. Định nghĩa tương tự với các điểm $B_c, B_a, C_a, C_b$. Gọi $I_1, I_2, I_3$ là tâm nội tiếp $\triangle AA_bA_c$, $\triangle BB_cB_a$, $\triangle CC_aC_b$. Chứng minh rằng $OI$ đi qua điểm Lemoine của $\triangle I_1I_2I_3$.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 2\\ \hline IHateMath & 1\\ \hline fatcat12345 & 2\\ \hline dogsteven & 3\\ \hline baopbc & 5\\ \hline QuangDuong12011998 & 1\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline\end{array}$$

Em cảm ơn thầy về ví dụ trên. Theo bản thân mình thấy bài này rất hay. Mong bạn Bảo theo nguyện vọng của mình, vẫn giữ nguyên bài 19, ai có lời giải thuần túy thì người đó được cộng thêm 3 điểm. Trong 2 ngày nữa, nếu không ai có lời giải thuần túy thì mình xin phép đăng lời giải bài mình đề xuất.

Anh Dương giỏi quá  , cảm ơn anh về lời giải. Cơ mà lời giải của em không cần dùng đến nghịch đảo đâu ạ, với lại đoạn chứng minh "$I$ là trọng tâm $\triangle ABC$" anh cũng không cần phải dùng đến vecto đâu ạ.

Cấu hình của bài thầy Hà trong bài đề nghị của Khánh là cấu hình rất thú vị, trên đó khai thác được khá nhiều điểm đặc biệt các tam giác $AA_bA_c,BB_cB_a,CC_aC_b$ mà những tâm đặc biệt của tam giác tạo bởi các tâm trên nằm trên đường thẳng $OI$ của $ABC$.

 

Mình ví dụ một bài như sau

 

Giữ nguyên đề của Khánh. Gọi $O_a,O_b,O_c$ là tâm ngoại tiếp tam giác $AA_bA_c,BB_cB_a,CC_aC_b$. Chứng minh rằng trọng tâm tam giác $O_aO_bO_c$ nằm trên đường thẳng $OI$ của $ABC$.

Còn ví dụ của thầy thì lại khá đơn giản: Gọi $O_{bc}, O_{ca}, O_{ab}$ lần lượt là trung điểm $O_bO_c, O_cO_a, O_aO_b$. Khi đó ta có $IO_{bc} \parallel OO_a, IO_{ca} \parallel OO_b, IO_{ab} \parallel OO_c$. Từ đó ta có trọng tâm $G$ của $\triangle O_aO_bO_c$ thuộc $OI$ và $\frac{\overline{GO}}{\overline{GI}} = -2$.

$\boxed{\text{Lời giải bài toán 19}}$

Bổ đề 1 (1đ): $I$ là trọng tâm tam giác $\triangle I_1I_2I_3$

Gọi $D, E, F$ thứ tự là tiếp điểm của $(I)$ với $BC, CA, AB$ và $X, Y, Z$ thứ tự là tiếp điểm của $A_bA_c, B_cB_a, C_aC_b$ với $(I)$.

Gọi $S(X)$ là ảnh của hình $X$ qua phép đối xứng tâm $I$.

Ta có $B_a = FF \cap YY = S(ZZ) \cap S(EE) = S(ZZ \cap EE) = S(C_a)$. Vậy $B_a$ đối xứng $C_a$ qua $I$. $\triangle AB_aC_a$ có $AI$ là phân giác và trung tuyến nên $AI \perp B_aC_a$. Do $I$ là tâm bàng tiếp của hai tam giác $\triangle BB_aB_c, \triangle CC_aC_b$ nên $I_2B_aC_aI_3$ là hình thang vuông. Do đó $AI$ chứa đường trung bình của hình thang vuông $I_2B_aC_aI_3$ nên $AI$ đi qua trung điểm $I_2I_3$, hay $I_1I$ là trung tuyến $\triangle I_1I_2I_3$. Từ đó ta có $I$ là trọng tâm $\triangle I_1I_2I_3$ $\blacksquare$.

Bổ đề 2 (1,5đ)(Bổ đề chìa khóa): Cho $\triangle ABC$ với điểm $P$ bất kì nằm trong tam giác. $AP, BP, CP$ thứ tự cắt $BC, CA, AB$ tại các điểm $A_0, B_0, C_0$. Đường thẳng qua $P$ vuông góc $AP$ cắt $BC$ tại $A_1$. Định nghĩa tương tự với $B_1, C_1$. Gọi $P_0$ là liên hợp đẳng giác của $P$ đối với $\triangle A_0B_0C_0$. Khi đó $A_1, B_1, C_1$ thuộc cùng một đường thẳng vuông góc với $PP_0$.(Mathematical Reflections 2006). 

Chứng minh bổ đề 2: 

Gọi $\triangle DEF, \triangle D_0E_0F_0$ thứ tự là tam giác pedal của điểm $P, P_0$ đối với $\triangle A_0B_0C_0$. Từ giả thiết $PA_1 \perp PA_0$ và $E_0F_0 \perp PA_0$, ta có $PA_1 \parallel E_0F_0$. Nếu $PA_1$ cắt $C_0A_0, A_0B_0$ tại $Y, Z$ thì theo định lí Reim ta có $E, F, Y, Z$ đồng viên (do $D, E, F, D_0, E_0, F_0$ đồng viên).

Gọi $J_a$ là giao điểm của $EF$ và $PA_1$. Ta có $\widehat{A_1PE} = \widehat{PA_0E} = \widehat{PFE}$, do đó $A_1P$ là tiếp tuyến của $(PEF)$. $B_0C_0$ cắt $BC$ tại $S$, theo hàng điểm cơ bản thì  $A(SA_0C_0B_0)= (SA_0BC)=-1$, do đó $(A_1PYZ)=A_0(A_1PYZ)=A_0(SAC_0B_0)=A(SA_0C_0B_0)=-1$. Từ đó ta có $J_aP^2=J_aE.J_aF=J_aY.J_aZ$, do $(A_1PYZ)=-1$ nên $J_a$ là trung điểm $A_1P$. Gọi đường tròn pedal của $P, P_0$ đối với $\triangle A_0B_0C_0$ là $\Omega$. Ta có $P_{J_a/(P,0)} = J_aP^2=J_aE.J_aF=P_{J_a/\Omega}$. Do đó $J_a$ thuộc trục đẳng phương của đường tròn điểm $P$ và đường tròn $\Omega$. Định nghĩa tương tự với $J_b, J_c$ thì $\overline{J_aJ_bJ_c} \perp PP_0$. Để ý rằng $J_a, J_b, J_c$ là trung điểm $PA_1, PB_1, PC_1$. Từ đó ta có đpcm $\blacksquare$.

Đặc biệt hóa: Khi $P$ là trọng tâm $\triangle ABC$, ta có $P_0$ là điểm Lemoine của $\triangle A_0B_0C_0$. Khi đó ta có $PP_0$ đi qua điểm Lemoine $L$ của $\triangle ABC$. Hay $PL$ vuông góc với $\overline{A_1B_1C_1}$

Bổ đề 3 (Hiển nhiên): Cho $\triangle ABC$ với tâm nôi tiếp $I$, tâm ngoại tiếp $O$. Đường qua $I$ vuông góc $IA$ cắt $BC$ tại $A_1$, Định nghĩa tương tự với $B_1, C_1$. Khi đó $\overline{A_1B_1C_1} \perp OI$.

Quay lại bài toán 19(0,5đ): 

Dễ thấy rằng $\triangle B_aI_2B_c, \triangle C_aI_3C$ có các cạnh tương ứng song song nên $B_aC_a, BC, I_2I_3$ đồng quy tại $A_1$. Tương tự, $A_bC_b, I_1I_3, AC$ đông quy tại $B_1$ và $A_cB_c, I_1I_2, AB$ đông quy tại $C_1$. Áp dụng bổ đề 3 ta có $OI \perp \overline{A_1B_1C_1}$. Gọi $L$ là điểm Lemoine của $\triangle I_1I_2I_3$, với chú ý $I$ là trọng tâm $\triangle I_1I_2I_3$ ta có $IL \perp \overline{A_1B_1C_1}$. Từ đó $O, I, L$ thẳng hàng $\blacksquare$.

 

 

$\boxed{\text{Lời giải bài toán 20:}}$

Bổ đề: Cho tam giác $\triangle ABC$ và điểm $P$ bất kì. Gọi $l_a$ là đường thẳng đối xứng của $AP$ qua đường phân giác góc $\widehat{BAC}$. Định nghĩa tương tự với $l_b, l_c$. Khi đó $l_a, l_b, l_c$ đôi một song song $\Leftrightarrow$ $P \in (ABC)$.

Quay lại bài toán:

Gọi $M_a, \Omega_a$ là điểm Miquel của tứ giác toàn phần ${AB, AC, DB, DC}$. Định nghĩa tương tự vói $M_b, M_c, \Omega_b, \Omega_c$. Gọi $E = AD \cap BC, F = AB \cap CD, G = AC \cap BD$. Gọi $E_1, E_2, G_1, G_2$ thứ tự là tâm ngoại tiếp tam giác $\triangle EAB, \triangle ECD, \triangle GAB, \triangle GCD$, $S = E_1G_1 \cap E_2G_2$. 

Ta có $(SE_1, SE_2) \equiv (E_1G_1,E_2G_2) \equiv (FB, FC)$ (mod $\pi$) (do $E_1G_1 \perp FB$ và $E_2G_2 \perp FC$) $\equiv (M_bA, M_bD) \equiv (M_bE_1, M_bE_2)$ (mod $\pi$) (dễ thấy $\triangle M_bE_1A \stackrel{+}{\sim} \triangle M_bE_2D$). Do đó $S \in \Omega_b$. Tương tự $S \in \Omega_a$. Gọi $T$ là giao điểm thứ hai của $\Omega_b$ và $\Omega_a$. Ta sẽ chứng minh $T \in (M_aM_bM_c)$.

Xét phép nghịch đảo cực $M_a$ hợp với phép đối xứng trục phân giác $l$ góc $\widehat{AM_aD}$:

$I_{M_a}^{M_aA.M_aD} \circ Đ_l$ biến $A \leftrightarrow D$, $B \leftrightarrow C$ (dễ thấy do $\triangle M_aAB \stackrel{-}{\sim} \triangle M_aDC$), do đó biến $(M_aAB) \leftrightarrow CD$, $(M_aCD) \leftrightarrow AB$. hay $G \leftrightarrow F$. 

Do $G \leftrightarrow F$, $A \leftrightarrow D$, $D \leftrightarrow A$ nên $(FAD) \leftrightarrow (GDA)$, tương tự $(FBC) \leftrightarrow (GCB)$ nên $M_b = (FAD) \cap (FBC) \leftrightarrow M_c = (GAD) \cap (GBC)$. Theo định nghĩa, ảnh của tâm đường tròn $(M_aAB)$ tức $G_1$ là đối xứng của cực qua ảnh đường tròn đó qua phép nghịch đảo, tức là đối xứng của $M_a$ qua đường thẳng $DC$. Gọi $l_{M_a}$ là đường thẳng qua $M_a$ vuông góc $CD$, thế thì $M_aG_1$ và $l_{M_a}$ đẳng giác trong góc $\widehat{AM_aD}$, hơn nữa $M_aM_b, M_aM_c$ đẳng giác trong góc $AM_aD$, thế thì $M_aG_1$ và $l_{M_a}$ đảng giác trong $\triangle M_aM_bM_c$. Định nghĩa tương tự với $l_{M_b}$, ta cũng chứng minh được $l_{M_b}$ và $M_bE_1$ đăng giác trong $\triangle M_aM_bM_c$. Theo Bổ đề ta có: $M_aG_1$ cắt $M_bE_1$ tại một điểm thuộc $(M_aM_bM_c)$. Giả sử $X=M_aG_1 \cap M_bE_1$ thì $X \in (M_aM_bM_c)$.

Từ đó ta có $(TM_a, TM_b) \equiv (TM_a, TS) + (TS, TM_b) \equiv (G_1M_a, G_1S) + (E_1S, E_1M_b) \equiv (G_1M_a, E_1M_b) \equiv (XM_a, XM_b) \equiv (M_cM_a, M_cM_b)$ (mod $\pi$). Vậy $T \in (M_aM_bM_c)$, hay $\Omega_a, \Omega_b, (M_aM_bM_c)$ đồng quy. Tương tự thì ta có đpcm $\blacksquare$.

$\boxed{\text{Bài toán 21 (AoPS)}}$: Cho tứ giác $ABCD$ ngoại tiếp đường tròn $(I)$. Các đoạn thẳng $AI, BI, DI$ thứ tự cắt $(I)$ tại $A', B', D'$. Tia $CI$ cắt $(I)$ tại $C'$ thỏa mãn $I$ nằm giữa $C, C'$. $X = AC \cap A'C'$, $Y= BD \cap B'D'$. Chứng minh $XY$ tiếp xúc $(I)$. 

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 3\\ \hline IHateMath & 1\\ \hline fatcat12345 & 2\\ \hline dogsteven & 3\\ \hline baopbc & 5\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline\end{array}$$

Lời giải bài 26: 

Đặt $(a+b+c)(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) = t$, theo AM-GM ta suy ra $t \geq 9$. 

Theo Cauchy-Schwarz ta có:

$(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}) = \sqrt{[(a^2+b^2+c^2)+2(ab+bc+ca)][(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2})+2(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca})]} \geq \sqrt{(a^2+b^2+c^2)(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2})} + 2\sqrt{(ab+bc+ca)(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca})} = \sqrt{(a^2+b^2+c^2)(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2})} + 2\sqrt{(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})}$. 

Do đó $(a^2+b^2+c^2)(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}) \leq (t-2\sqrt{t})^2 = t(\sqrt{t}-2)^2$.

Điều đó có nghĩa ta chỉ cần chứng minh: 

$t \geq 1+2\sqrt[3]{6t(\sqrt{t}-2)^2+10}$ $\Leftrightarrow$ $t^3-51t^2+192t\sqrt{t}-189t-81 \geq 0$ $\Leftrightarrow$ $(\sqrt{t}-3)^3(t\sqrt{t}+9t+3\sqrt{t}+3) \geq 0$ (luôn đúng với mọi $t \geq 9$). Ta có đpcm $\blacksquare$.

P/s: bạn nào post bài mới hộ mình đi, mình chưa có bài đề xuất nào.

Ngoài tính chất trên thì có rất nhiều tính chất thú vị khác cũng đúng! Sau đây là các phát biểu của anh Dương gửi cho em!

Cho $P,Q$ đẳng giác trong tam giác $ABC$. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA,AB$ tại $P_{ac},P_{ab}$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA,AB$ tại $Q_{ac},Q_{ab}$. Thì $P_{ac},P_{ab},Q_{ac},Q_{ab}$ cùng thuộc một đường tròn $(O_a)$ tiếp xúc $(O)$ tại $A_a$. Tương tự có $B_b,C_c$.

a) $AA_a,BB_b,CC_c$ đồng quy tại $I$.

b) Gọi $O_a,O_b,O_c$ lần lượt là tâm các đường tròn tiếp xúc với $(O)$. Chứng minh rằng $AO_a,BO_b,CO_c$ đồng quy tại $J$.

c) Chứng minh rằng $O,I,J$ thẳng hàng.

Post 193.png

Hình vẽ

Xin phép được chứng minh toàn bộ tính chất Bảo đưa ra và một tính chất thầy Hùng đăng ở post #15:

Anh Dương đã chứng minh $(O_a)$ tiếp xúc $(O)$, em xin được chứng minh theo cách khác không dùng chứng minh trùng .

Trước hết, gọi $A_a = (BPP_{ab}) \cap (ABC)$. Ta có $(PP_{ac}, PA_a) \equiv (PP_{ab}, PA_a) \equiv (BP_{ab}, BA_a) \equiv (BA, BA_a) \equiv (CA, CA_a) \equiv (CP_{ac}, CA_a)$ (mod $\pi$), do đó $C, P, P_{ac}, A_a$ đồng viên. Gọi $R = BP \cap CQ$. Ta có $(PR, PP_{ac}) \equiv (PB, PP_{ab}) \equiv (CB, CP)$ (do $PP_{ab}$ là tiếp tuyến $(PBC)$) $\equiv (CQ, CA)$ (do $P, Q$ đẳng giác) $\equiv (CR, CP_{ac})$ (mod $\pi$). Do đó $C, P, P_{ac}, A_a, R$ đồng viên. Gọi $S= BQ \cap CP$ thì tương tự ta có $S \in (BP_{ab}PA_a)$. 

Ta có $(QQ_{ac}, QS) \equiv (QQ_{ab}, QB) \equiv (CQ, CB)$ (do $QQ_{ab}$ là tiếp tuyến $(QBC)$) $\equiv (CA, CP) \equiv (CQ_{ac}, CS)$ (mod $\pi$) nên $C, Q, S, Q_{ac}$ đồng viên. Tương tự $B, Q, R, Q_{ab}$ đồng viên. Do $A_a$ là điểm Miquel của tứ giác toàn phần $PRQSBC$ nên $A_a \in (CQ_{ac}QS), A_a \in (BQ_{ab}QR)$. Ta lại có $(RQ_{ab}, RB) \equiv (QQ_{ab}, QB) \equiv (QQ_{ac}, QS) \equiv (CQ_{ac}, CS) \equiv (CP_{ac}, CP) \equiv (RP_{ac}, RP) \equiv (RP_{ac}, RB)$ (mod $\pi$). Do đó $Q_{ab}, R, P_{ac}$ thẳng hàng. Tương tự thì $P_{ab}, S, Q_{ac}$ thẳng hàng. Do đó $(P_{ac}Q_{ab}, P_{ac}Q_{ac}) \equiv (P_{ac}R, P_{ac}C)  \equiv (PR, PC) \equiv (PB, PS) \equiv (P_{ab}B, P_{ab}S) \equiv (P_{ab}Q_{ab}, P_{ab}Q_{ac})$ (mod $\pi$). Do đó $P_{ab}, P_{ac}, Q_{ab}, Q_{ac}$ đồng viên. Từ đó ta cũng có $(A_aB, A_aQ) \equiv (Q_{ab}B, Q_{ab}Q) \equiv (Q_{ab}P_{ab}, Q_{ab}Q_{ac}) \equiv (P_{ac}P_{ab}, P_{ac}Q_{ac}) \equiv (P_{ac}P, P_{ac}C) \equiv (A_aP, A_aC)$ (mod $\pi$). Do đó $A_aP, A_aQ$ đẳng giác trong góc $\widehat{BA_aC}$. 

Ta có $(A_aP_{ab}, A_aQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (A_aQ, A_aQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (SQ, SQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (SB, SP_{ab}) \equiv (A_aP_{ab}, A_aQ) + (A_aB, A_aP_{ab}) \equiv (A_aB, A_aQ) \equiv (Q_{ab}B, Q_{ab}Q) \equiv (Q_{ab}P_{ab}, Q_{ab}Q_{ac})$ (mod $\pi$). Do đó $A_a \in (P_{ab}P_{ac}Q_{ab}Q_{ac})$. Kẻ tiếp tuyến $A_ax$ của $(ABC)$. Ta có $(A_aP_{ab}, A_ax) \equiv (A_aP_{ab}, A_aB) + (A_aB, A_ax) \equiv (PP_{ab}, PB) + (CB, CA_a) \equiv (CP, CB) + (CB, CA_a) \equiv (CP, CA_a) \equiv (P_{ac}P, P_{ac}A_a) \equiv (P_{ac}P_{ab}, P_{ac}A_a)$ (mod $\pi$). Do đó $A_ax$ cũng là tiếp tuyến $(A_aP_{ab}P_{ac}Q_{ac}Q_{ab})$. Do đó $(O_a)$ tiếp xúc $(O)$ tại $A_a$. 

Bây giờ ta sẽ chứng minh bài của Bảo: 

a) Ta sẽ sử dụng bổ đề Ceva trong đường tròn: Cho $\triangle ABC$ nội tiếp $(O)$, các điểm $A', B', C'$ bất kì chạy trên $(O)$. Khi đó $AA', BB', CC'$ đồng quy $\Leftrightarrow$ $\frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B} = 1$.

Quay lại bài toán:

Ta đã có $(A_aB, A_aQ) \equiv (A_aP, A_aC)$ (mod $\pi$), mà $(QA_a, QB) \equiv (QA_a, QS) \equiv (CA_a, CS) \equiv (CA_a, CP)$ (mod $\pi$). Do đó $\triangle A_aBQ \stackrel{+}{\sim} \triangle A_aPC$. Tương tự $\triangle A_aBP \stackrel{+}{\sim} \triangle A_aQC$. Với hai cặp tam giác đồng dạng cùng hướng ta có $\frac{A_aB}{A_aC} = \frac{A_aB}{A_aP}.\frac{A_aP}{A_aC} = \frac{BQ}{PC}.\frac{BP}{QC} = \frac{BP.BQ}{CP.CQ}$.   

Khi định nghĩa tương tự với $B_b, C_c$, do sự hoán vị vòng quanh nên ta có ngay $\frac{A_aB}{A_aC}.\frac{B_bC}{B_bA}.\frac{C_cA}{C_cB}=1$. Ta có đpcm $\blacksquare$.

Trước khi chứng minh phần b) và c) của bài toán, mình sẽ chứng minh tính chất $B_bC_c, O_bO_c, BC$ đông quy.

Trước hết ta có $(A_aP_{ab}, A_aB) \equiv (PP_{ab}, PB) \equiv (CP, CB)$ (mod $\pi$). Do đó $A_aP_{ab}$ cắt $CP$ tại một điểm $C_p$ thuộc $(O)$. Tương tự định nghĩa như vậy với $A_p, B_p, A_q, B_q, C_q$.

$B_bC_c$ cắt $BC$ tại $A_1$. Dễ dàng chứng minh được $Q_{ca}Q_{cb} \parallel B_qA_q$. Do đó $(B_bC_c, B_bQ_{bc}) \equiv (B_bC_c, B_bA_q) \equiv (B_qC_c, B_qA_q) \equiv (Q_{ca}C_c, Q_{ca}Q_{cb}) \equiv (P_{cb}C_c, P_{cb}Q_{cb}) \equiv (P_{cb}C_c, P_{cb}Q_{bc})$ (mod $\pi$). Do đó $B_b, C_c, Q_{bc}, P_{cb}$ đồng viên. Tương tự $B_b, C_c, Q_{cb}, P_{bc}$ đồng viên.

Xét phép nghịch đảo cực $A_1$ biến $B_b \leftrightarrow C_c$, $P_{cb} \leftrightarrow Q_{bc}$, $P_{bc} \leftrightarrow Q_{cb}$. Do đó $(O_b) \leftrightarrow (O_c)$. Do đó $A_1, O_b, O_c$ thẳng hàng hay $B_bC_c, O_bO_c, BC$ đồng quy $\blacksquare$.

b) Định nghĩa: Cho $\triangle ABC, \triangle DEF$ có $AD, BE, CF$ đồng quy tại $M$ thì $M$ gọi là tâm phối cảnh của hai tam giác $\triangle ABC, \triangle DEF$. Và nếu $X = AB \cap DE, Y =BC \cap EF, Z =CA \cap FD$ thì $\overline{XYZ}$ gọi là trục phối cảnh của hai tam giác $\triangle ABC, \triangle DEF$.

Ta có nếu định nghĩa tương tự với $B_1, C_1$ tương tự $A_1$ thì do $\triangle O_aO_bO_c, \triangle A_aB_bC_c$ nhận $O$ là tâm phối cảnh nên $\overline{A_1B_1C_1}$ là trục phối cảnh của $\triangle A_aB_bC_c$ và $\triangle O_aO_bO_c$. Do tính chất đồng quy và chứng minh trên: $B_bC_c, O_bO_c, BC$ đồng quy, nên $\overline{A_1B_1C_1}$ là trục phối cảnh của $\triangle ABC$ và $\triangle O_aO_bO_c$. Do đó $AO_a, BO_b, CO_c$ đồng quy tại $J$.

c) Ta sử dụng bổ đề sau. Cho $\triangle ABC, \triangle MNP, \triangle XYZ$ có chung trục phối cảnh. Khi đó 3 tâm phối cảnh của $\triangle ABC, \triangle MNP , \triangle XYZ$ thẳng hàng. (Điều này dễ dàng chứng minh được nhờ Pappus, Menelaus như khi mình chứng minh định lí Desargues). 

Xét tam giác $\triangle ABC, \triangle O_aO_bO_c, \triangle A_aB_bC_c$ có chung trục phối cảnh nên 3 tâm phối cảnh $O, I, J$ thẳng hàng $\blacksquare$. 

Một chất chất khác giống điểm Nagel mà em vừa tìm thấy như sau:

Gọi $G$ là trọng tâm $\triangle ABC$, $M$ là trung điểm $PQ$ và $I*$ là liên hợp đẳng giác của $I$ (đồng quy của $AA_a, BB_b, CC_c$) thì $\overrightarrow {GI*} = 2\overrightarrow{MG}$ 

Theo em thấy thì ý tưởng của các lời giải trên có thể chứng minh bài này.
Dễ thấy $Q, R$ là trung điểm $BM, CN$, nên $Q, O, R$ thẳng hàng và là trục đối xứng của hình chữ nhật $ABCD$. $AQ$ cắt $DR$ tại $X$. $SQ, TR$ thứ tự cắt $AC, BD$ tại $Y, Z$ thì $Q, R$ thứ tự là trung điểm $SY, TZ$. Do đó $QK \parallel AC$ và $RK \parallel BD$ do đó $\widehat{QKR}=\widehat{AOD}=\widehat{AXD}=\widehat{QXR}$. Hơn nữa $SQRT$ là hình thang vuông nên dễ thấy $\triangle QKR$ cân tại $K$. Do đó ta có ngay $K$ là tâm của đường tròn $(XQR)$. $AQ, DR$ thứ tự cắt $BC$ tại $E, F$. Dễ thấy $DCFN$ là hình chữ nhật nên $TZ$ cũng là trung trực $CF$. Do đó $\triangle TCF$ cân tại $T$. Hay ta có $TF \parallel BD$. Tương tự $SE \parallel AC$. Nếu $SE$ cắt $TF$ tại $H$ thì ta cũng suy ra $H$ là tâm ngoại tiếp $\triangle XEF$. Do $EF \parallel QR$ nên $X, H, K$ thẳng hàng. Mặt khác $SHTO$ là hình bình hành nên $H, K, O$ thẳng hàng. Do đó $O, K, X$ thẳng hàng. Ta có đpcm.

$\boxed{\text{Lời giải bài 27}}$
Gọi $O$ là tâm đường tròn ngoại tiếp $\triangle ABC$. Đương nhiên $KH$ cắt $AO$ tại $F$ thuộc $(O)$. Gọi $I$ là tâm đường tròn ngoại tiếp $\triangle BHC$. Tiếp tuyến tại $H$ của $(I)$ cắt $AC$ tại $J$. Ta có $\widehat{AJH}+\widehat{CAF} = \widehat{ACH}+\widehat{JHC}+\widehat{CAF}=\widehat{ABH}+\widehat{HBC}+90°-\widehat{ABC}=90°$. Do đó $HJ \perp AF$, nên $HI \parallel AO$. Gọi $M$ là giao điểm của $HI$ và $KO$ thì $\triangle MHK$ cân tại $M$. Ta cũng có đường tròn $(M;MK)$ tiếp xúc trong $(O)$ tại $K$ và tiếp xúc ngoài $(I)$ tại $H$. Theo định nghĩa về tâm đăng phương thì tiếp tuyến tại $K$ của $(O)$, tiếp tuyến tại $H$ của $(BHC)$ và $BC$ đồng quy tại $S$. Ta có do $HD, HE$ đẳng giác góc $\widehat{BHC}$ nên $SH$ tiếp xúc $(HDE)$ do đó $SK^2=SH^2=SD.SE$ nên $SK$ tiếp xúc $(KDE)$. Do $SK$ tiếp xúc $(O)$ nên ta có đpcm.
P/s: một bạn đề xuất bài mới giúp mình được không ạ?

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 4\\ \hline IHateMath & 1\\ \hline fatcat12345 & 3\\ \hline dogsteven & 4\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline halloffame & 1\\ \hline\end{array}$$