$\boxed{1}$ Kể từ thời Trung Cổ, $2013$ là năm đầu tiên chứa bốn số liên tiếp nhau. Hỏi có bao nhiêu năm như vậy, kể từ năm $2013$ đến trước năm $10000$ ?
$\boxed{2}$ Tìm tất cả các cặp $(A,B)$ trong đó $A$ là số có $2$ chữ số, $B$ là số có $3$ chữ số thỏa mãn $A$ tăng lên $B$% sẽ bằng $B$ giảm $A$%.
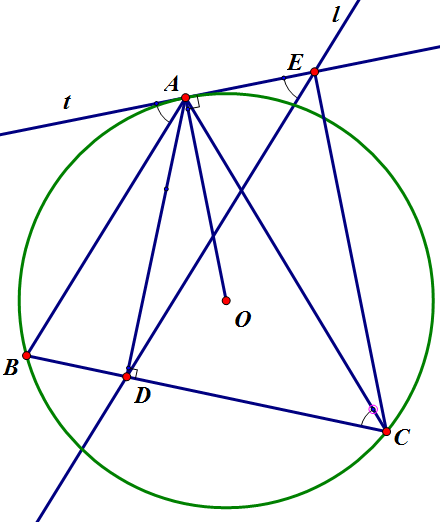
$\boxed{3}$ Cho tam giác nhọn $ABC$, $AD$ là đường cao từ $A$ hạ xuống $BC$. Đường thẳng $l$ đi qua $D$ song song $AB$, $t$ là tiếp tuyến đường tròn ngoại tiếp $ABC$ tại $A$. Gọi $E$ là giao điểm của $l$ và $t$. Chứng minh $CE$ vuông góc với $t$.
$\boxed{4}$ Tìm tất cả các đa thức $f,g$ có hệ số thực thỏa mãn:
$\boxed{5}$ Đặt một số đồng xu lên bảng có $20\times 13$ ô. Hai đồng xu được gọi là láng giềng nếu chúng được đặt cùng hàng hoặc cột và giữa chúng không có đồng xu nào. Hỏi số đồng xu lớn nhất có thể đặt lên bảng sao cho không đồng xu nào có hơn 2 đồng xu láng giềng?
$\boxed{6}$ Cho tam giác nhọn $ABC$ với $AC\neq BC$, $O$ là tâm đường tròn ngoại tiếp $ABC$ và $F$ là chân đường cao hạ từ $C$. Kéo dài $CO$, ta hạ đường cao $AX$ và $BY$. $FO$ cắt đường tròn ngoại tiếp tam giác $FXY$ tại điểm thứ $2$ là $P$. Chứng minh rằng: $OP<OF$.
Translate by funcalys