Chủ đề này có 3 trả lời

[LongKa]

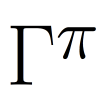
Chứng minh:

\[\sum_{n = 0}^{\infty} \dfrac{C_{2n}^{n} }{2^{2n}} a^{3n} = \dfrac{1}{\sqrt{1 - a^3}}\]

với 0 < a < 1 và $C_{2n}^{n}$ là tổ hợp chập $n$ của $2n$.

[Mrnhan]

Chứng minh:

\[\sum_{n = 0}^{\infty} \dfrac{C_{2n}^{n} }{2^{2n}} a^{3n} = \dfrac{1}{\sqrt{1 - a^3}}\]

với 0 < a < 1 và $C_{2n}^{n}$ là tổ hợp chập $n$ của $2n$.

 

Lời giải.

 

Ta có nhận xét sau:

 

$$\Gamma(n+\frac{1}{2})=\int_{0}^{\infty} x^{n-\frac{1}{2}}e^{-x}dx=\frac{(2n!)}{2^{2n}n!\sqrt{\pi}}$$

 

$$\Rightarrow \frac{C_{2n}^{n}a^{3n}}{2^{2n}}=\int_{0}^{\infty}\frac{x^{-\frac{1}{2}}e^{-x}}{\sqrt{\pi}}\frac{(xa^3)^n}{n!}dx$$

 

$$\Rightarrow\sum_{n=0}^{\infty} \frac{C_{2n}^{n}a^{3n}}{2^{2n}}=\int_{0}^{\infty}\frac{x^{-\frac{1}{2}}e^{-x}}{\sqrt{\pi}}\sum_{n=0}^{\infty}\frac{(xa^3)^n}{n!}dx=\frac{1}{\sqrt{\pi}}\int_{0}^{\infty}x^{-\frac{1}{2}}e^{-x(1-a^3)}dx$$

 

$$=\frac{1}{\sqrt{\pi(1-a^3)}}\int_{0}^{\infty}x^{-\frac{1}{2}}e^{-x}dx=\frac{\Gamma(\frac{1}{2})}{\sqrt{\pi(1-a^3)}}=\frac{1}{\sqrt{1-a^3}}$$

 

 

Bài viết đã được chỉnh sửa nội dung bởi Mrnhan: 17-05-2015 - 10:19

[chanhquocnghiem]

Chứng minh:

\[\sum_{n = 0}^{\infty} \dfrac{C_{2n}^{n} }{2^{2n}} a^{3n} = \dfrac{1}{\sqrt{1 - a^3}}\]

với 0 < a < 1 và $C_{2n}^{n}$ là tổ hợp chập $n$ của $2n$.

Xét khai triển Mac Laurin của hàm $f(x)=\frac{1}{\sqrt{1-x}}$ (xác định và có đạo hàm mọi cấp trên $(0;1)$)

Đạo hàm cấp n là $f^{(n)}(x)=\frac{1.3.5...(2n-1)}{2^n}(1-x)^{-\frac{2n+1}{2}}\Rightarrow f^{(n)}(0)=\frac{1.3.5...(2n-1)}{2^n}$

$\Rightarrow \frac{1}{\sqrt{1-x}}=f(0)+\sum_{n=1}^{\infty}\frac{f^{(n)}(0)}{n!}\ x^n=1+\sum_{n=1}^{\infty}\frac{(2n)!}{2^{2n}.(n!)^2}\ x^n=1+\sum_{n=1}^{\infty}\frac{C_{2n}^{n}}{2^{2n}}\ x^n$

Nếu quy ước $C_{0}^{0}=1$ thì ta có thể viết gọn : $\sum_{n=0}^{\infty}\frac{C_{2n}^{n}}{2^{2n}}\ x^n=\frac{1}{\sqrt{1-x}}$

Vì $a^3\in (0;1)$ nên ta có $\sum_{n=0}^{\infty}\frac{C_{2n}^{n}}{2^{2n}}\ a^{3n}=\frac{1}{\sqrt{1-a^3}}$

 

Mở rộng : Với $a\in (0;1)$ và $\alpha$ là số thực dương, ta có $a^\alpha \in (0;1)$, do đó $\sum_{n=0}^{\infty}\frac{C_{2n}^{n}}{2^{2n}}\ a^{\alpha n}=\frac{1}{\sqrt{1-a^\alpha }}$

Bài viết đã được chỉnh sửa nội dung bởi chanhquocnghiem: 17-05-2015 - 18:55

[hxthanh]

\begin{align*} (1-x^3)^{-\frac{1}{2}}=\sum_{n=0}^\infty{-\frac{1}{2}\choose n}(-x^3)^n &=\sum_{n=0}^\infty\dfrac{\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)...\left(-\frac{2n-1}{2}\right)}{n!}(-1)^nx^{3n}\\ &=\sum_{n=0}^\infty\dfrac{(2n-1)!!(2n)!!}{(2n)!!2^n.n!}x^{3n} \\ &=\sum_{n=0}^\infty\dfrac{1}{2^{2n}}{2n\choose n}x^{3n}\end{align*}