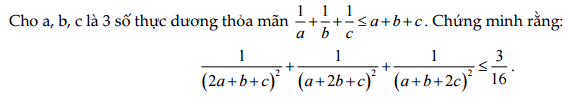Chủ đề này có 2 trả lời

[Drago]

[IHateMath]

Bài này tương tự bài toán $\text{A2 IMO 2009 Shortlist}$, chỉ thay điều kiện $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=a+b+c$. Lời giải cũng tương tự như bài toán nói trên.

[Drago]

Theo đáp án của $ A2 IMO 2009 Shortlist $ thì có 2 cách:
Cách 1:
Với $x,y,z$ là các số thực dương, theo bất đẳng thức $AM-GM$ ta có:
     $2x+y+z=(x+y)+(x+z) \geq 2\sqrt{(x+y)(x+z)}$
nên ta được:
     $\frac{1}{\left ( 2x+y+z \right )^2}\leq \frac{1}{4(x+y)(x+z)}$
 
Suy ra:
     $\sum _{x,y,z}\frac{1}{\left ( 2x+y+z \right )^2}\leq \sum _{x,y,z}\frac{1}{4(x+y)(x+z)}=\frac{a+b+c}{2(a+b)(b+c)(c+a)}$             $(1)$                                                                                                                                                            
Giả thiết $\sum_{x,y,z} \frac{1}{a}=\sum_{x,y,z} a$ có thể viết lại như sau:
     $ab+bc+c=abc(a+b+c)$                                                                                                       $(2)$
 
Ta cũng có hai BĐT quen thuộc $(ab+bc+ca)^2 \geq 3abc(a+b+c)$                                        $(3)$
                                                   $9(a+b)(b+c)(c+a) \geq 8(a+b+c)(ab+bc+ca)$                       $(4)$
 
Kết hợp $(1),(2),(3)$ và $(4)$, ta kết thúc chứng minh:
     $\frac{a+b+c}{2(a+b)(b+c)(c+a)}=\frac{\left ( a+b+c \right )\left ( ab+bc+ca \right )}{2(a+b)(b+c)(c+a)}.\frac{ab+bc+ca}{abc(a+b+c)}.\frac{abc(a+b+c)}{\left (ab+bc+ca \right )^2}\leq \frac{9}{2.8}.1.\frac{1}{3}=\frac{3}{16}$  
 

P/s: lười gõ quá, đành đăng cách 2 bằng ảnh, ai chỉ mình cách spoiler đoạn này vs 

 

                                                                                                          

Bài viết đã được chỉnh sửa nội dung bởi Drago: 18-06-2017 - 10:22