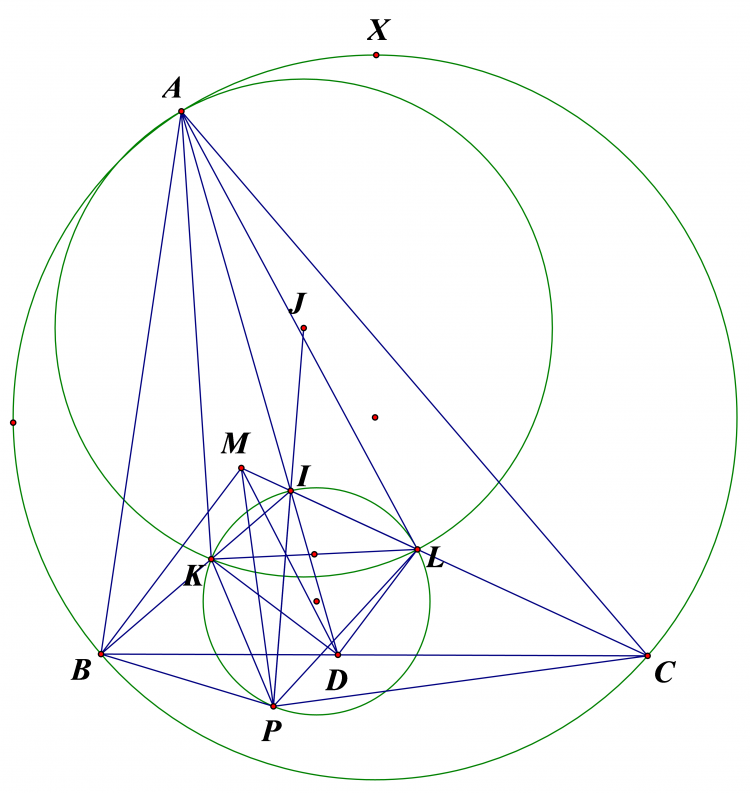
lời giải bài 2 của em
Bổ đề 1 : Cho tam giác $ABC$,trung điểm cung $AC$ không chứa $B$ là $X$ trung điểm $BC$ là $M$. Đường đối trung $AK$. Chứng minh rằng nếu $X$ là tâm của $\odot (ACM)$ thì $AX \perp AK$
Chưng minh. Ta có $BX$ là phân giác $\angle{ABC}$. Mà $\angle{BMA}=\frac{\angle{AXC}}{2}=90-\frac{\angle{ABC}}{2}=90-\angle{XBM}$ vậy $BX \perp AM$
Vậy $90-\angle{CAX}=\frac{\angle{AXC}}{2}=\angle{BMA}=\angle{MAB}=\angle{KAC}$ Suy ra $AK \perp AX$
Bổ đề 2: Cho tam giác $ABC$ nội tiếp $\odot(O)$. Đường kính $AX$, tiếp tuyến tại $X$ cắt $BC$ tại $K$. Giao của $KO$ và $AB,AC$ là $D,E$. Chứng minh rằng $O$ là trung điểm $DE$.
Chứng minh. (Bổ đề này quen thuộc)
Quay lại bài toán:
Ta gọi đường kính của $\odot(O)$ là $AX$. Tiếp tuyến tại $X$ cắt $BC$ tại $L$. Vậy theo bổ đề 2 thì $E,D,O,K$ thẳng.
Gọi giao của $DE$ và $\odot(O)$ là $Y,Z$ sao cho $Y$ nằm trên cung $AC$ từ gia thiết $DE=OA$ suy ra $OD=DY$. Giao của $YC$ và đường thẳng qua $O$ song song $AC$ thì $M'$ thì ta có $CM'=CY$ tương tự ta có điềm $N'$ và $BN'=BZ$. Vậy theo E.R.I.Q thì $K$ là trung điểm $M'N'$. Gỉa sử tồn tại $U,V$ khác $M',N'$ và nhận $K$ là trung điểm suy ra hình bình hành vố lí vậy $M'$ trùng $M$ và $N'$ trùng $N$.
Vậy ta có $\angle{OMC}=\angle{ACY}=\angle{AXY}$. Vậy $O,X,M,Y$ thuộc 1 đường tròn tương tự $O,X,N,Z$ thuộc 1 đường tròn.
Vậy theo Miquel thì $P,M,N,X$ thuộc 1 đường tròn.
Áp dụng Pascal cho 5 điểm $X,B,C,Y,Z$. Gọi giao của $BY$ và $XC$ là $G$. Giao của $CZ$ và $XB$ là $H$ thì $G,K,H$ thẳng. Gọi giao của $BY$ và $CZ$ $T$ vậy áp dụng Desargues suy ra $TX$,$YC$,$BZ$ đồng qui.tại $P$. Vậy $PX \perp DE$ suy ra $\angle{CPX}=90-\angle{OYC}=\angle{CXY}$
Áp dụng bổ đề 1 cho $\triangle YXM$ thì ta suy ra $XK$ là đường đối trung của vậy $\angle{MXL}=\angle{CXY}=\angle{CPX}$ vậy ta suy ra $LX$ là tiếp tuyến của $\odot(PMN)$ mà $LX$ là tiếp tuyến của $\odot(O)$ vậy ta suy ra $\odot (O)$ tiếp xúc $\odot (PMN)$
Bài viết đã được chỉnh sửa nội dung bởi NHN: 09-10-2017 - 16:55