Ký hiệu $r,R$ lần lượt là bán kính của đường tròn nội tiếp và ngoại tiếp $\Delta ABC$
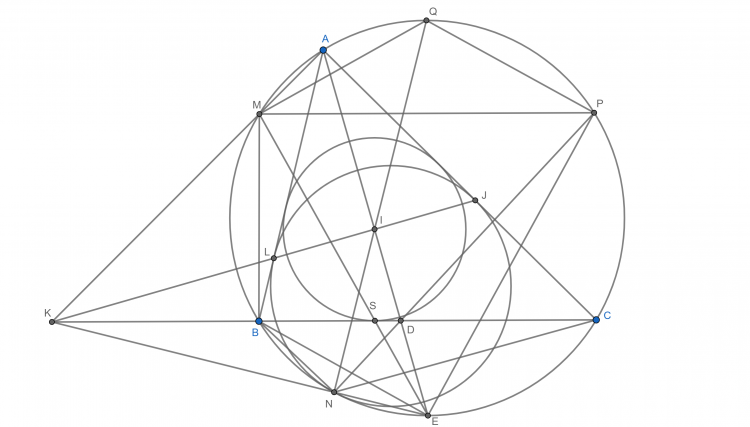
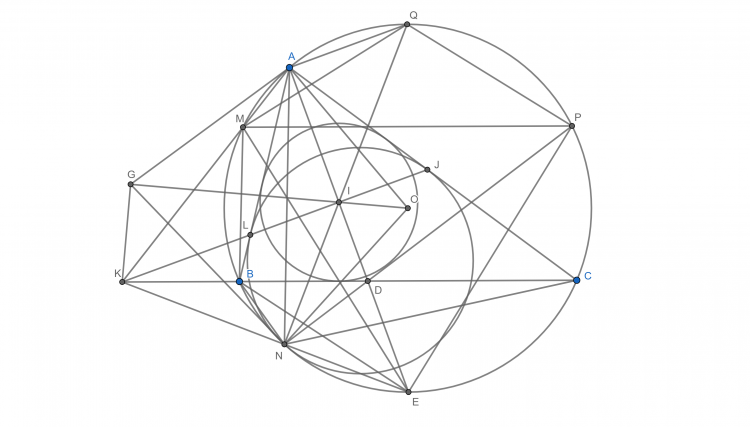
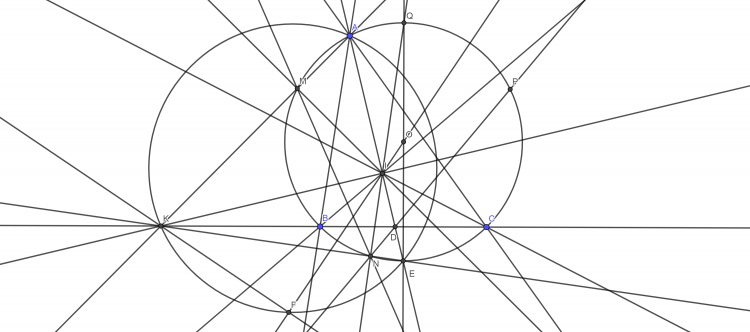
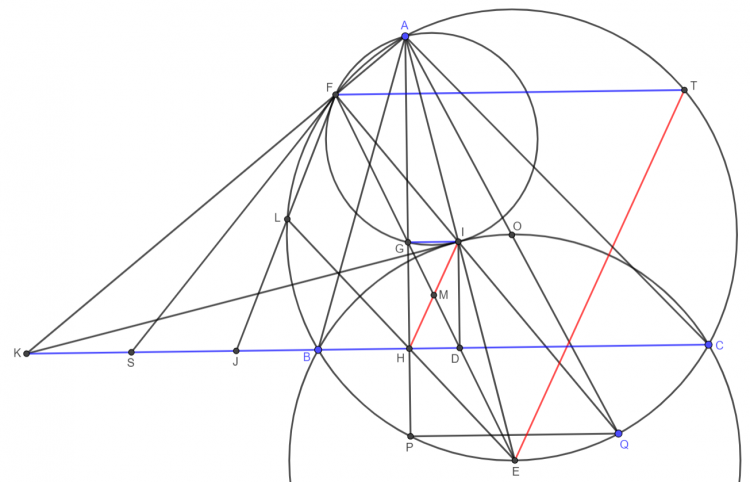
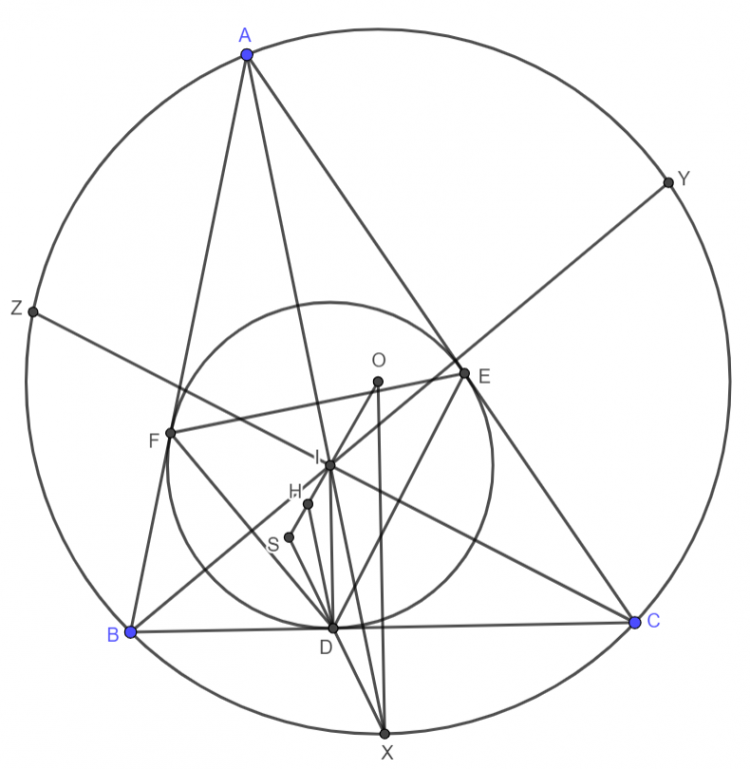
Bổ đề: Cho $\Delta ABC$ nội tiếp đường tròn ($O$) và ngoại tiếp đường tròn ($I$). $D,E,F$ lần lượt là tiếp điểm của ($I$) trên $BC,CA,AB$. Khi đó $OI$ là đường thẳng Euler của $\Delta DEF$
Cm: $AI,BI,CI$ lần lượt cắt lại ($O$) tại điểm thứ $2$ là $X,Y,Z$ thì $X,Y,Z$ lần lượt là điểm chính giữa cung $BC$ ko chứa $A$, cung $CA$ ko chứa $B$, cung $AB$ ko chứa $C$ của đường tròn ($O$)
Dễ thấy $OX\parallel ID$. $XD$ cắt $OI$ tại $S$. Theo định lý Thales: $\dfrac{SD}{SX}=\dfrac{SI}{SO}=\dfrac{r}{R} \Rightarrow S$ cố định. Tương tự $YE,ZF$ cũng đi qua $S$
Lấy điểm $H\in SO$ thỏa mãn $\dfrac{SH}{SI}=\dfrac{r}{R} \Rightarrow H$ cố định. Mà $\dfrac{SD}{SX}=\dfrac{r}{R}$ nên theo định lý Thales đảo thì $DH\parallel XI$ hay $DH\perp EF$
Tương tự $EH\perp FD$ và $FH\perp DE$. Từ đó $H$ là trực tâm của $\Delta DEF \Rightarrow \overline{I,H,O}$ là đường thẳng Euler của $\Delta DEF \Rightarrow$ đpcm
Trở lại bt:
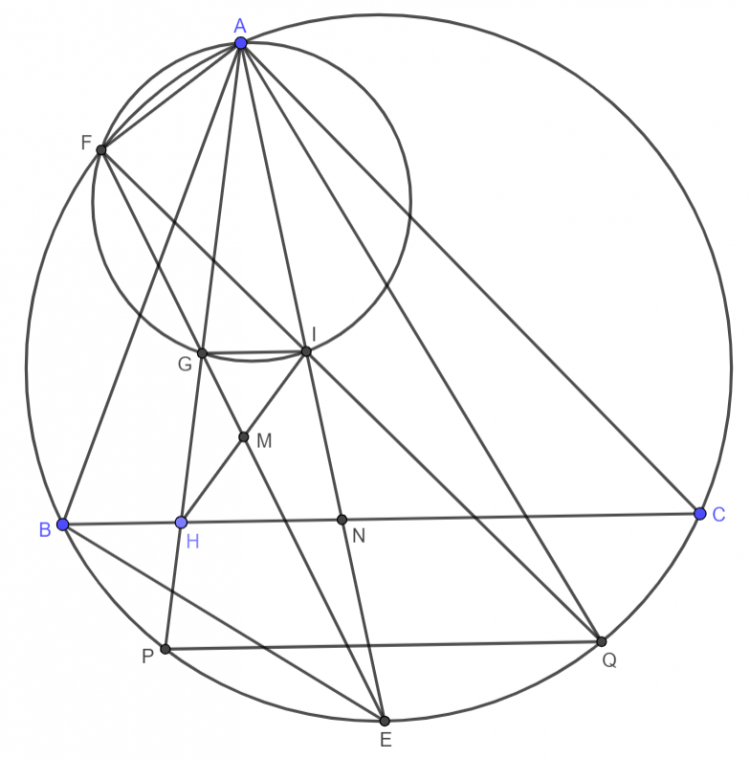
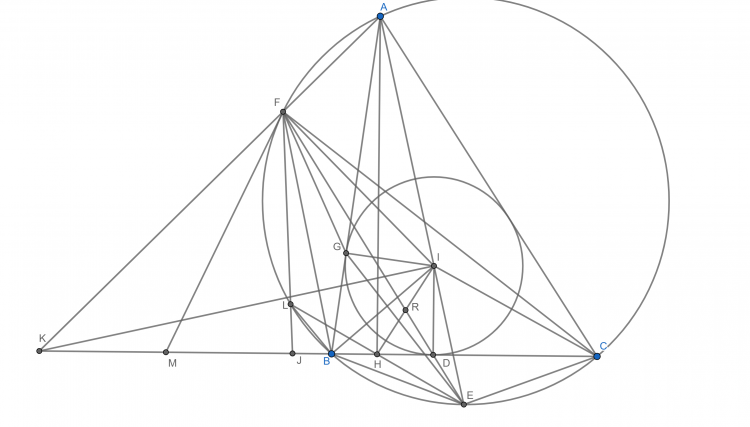
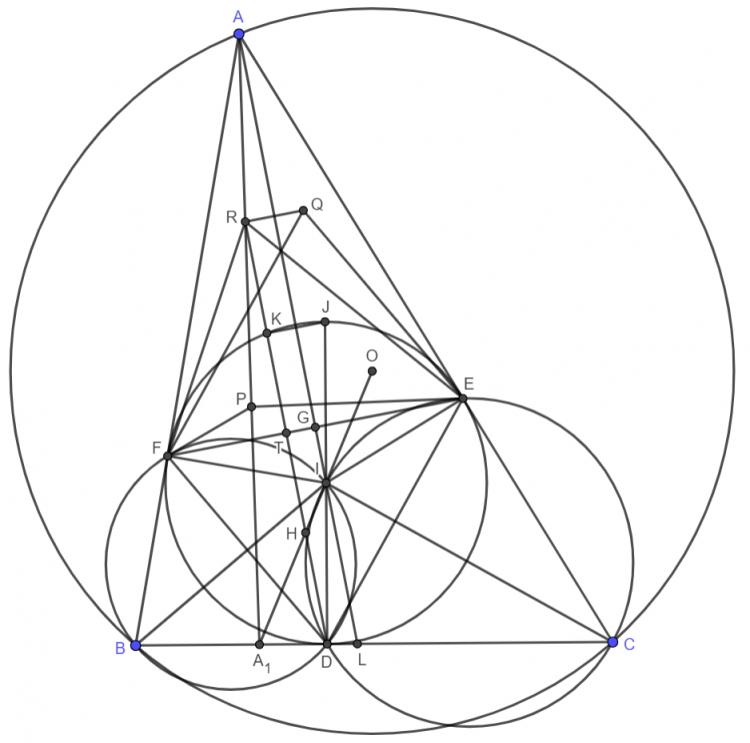
Gọi $D$ là tiếp điểm của ($I$) trên $BC \Rightarrow D$ thuộc ($IEC$) và ($IFB$). Gọi $Q$ là điểm liên hợp đẳng giác của $P$ trong $\Delta AEF$, $R$ là điểm đối xứng với $Q$ qua $AI \Rightarrow \overline{A,R,P}$
Ta có biến đổi góc: $\angle QEF=\angle AEP=\angle EIC=\dfrac{\angle EID}{2}=\angle DFE \Rightarrow QE\parallel DF$. Tương tự: $QF\parallel DE$
$\Rightarrow QEDF$ là hình bình hành $\Rightarrow QE=DF$ và $QF=DE$. Dễ thấy $RQEF$ là hình thang cân $\Rightarrow RF=QE$ và $RE=QF$
Nên $EF$ là đường trung trực của $DR$ hay $R$ đối xứng với $D$ qua $EF$
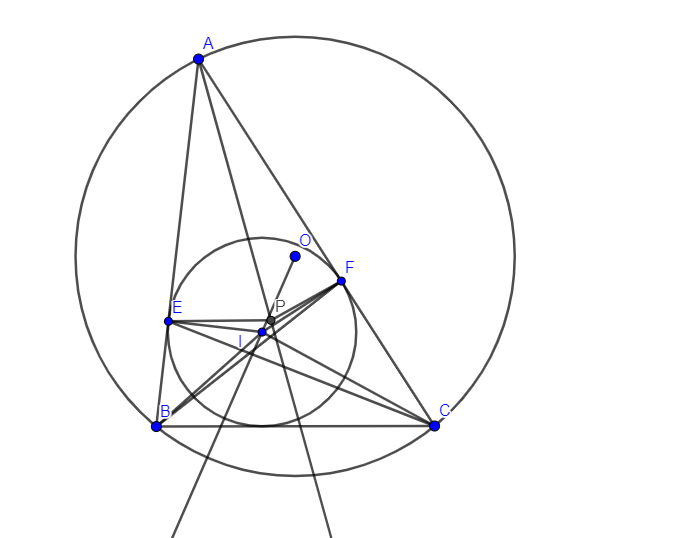
$AI$ cắt $EF,BC$ lần lượt tại $G,L$. Kẻ đường kính $DJ$ của ($I$). $DR$ cắt $EF$ và cắt lại ($I$) lần lượt tại $T,K$. Gọi $H$ là điểm đối xứng với $K$ qua $T \Rightarrow H$ là trực tâm của $\Delta DEF$
$\Delta AEI \sim \Delta EGI \Rightarrow \dfrac{AI}{r}=\dfrac{r}{IG}=\dfrac{2r}{DH}$ ($1$)
$\Delta DKJ \sim \Delta IDL \Rightarrow \dfrac{2r}{DK}=\dfrac{IL}{r}$ ($2$)
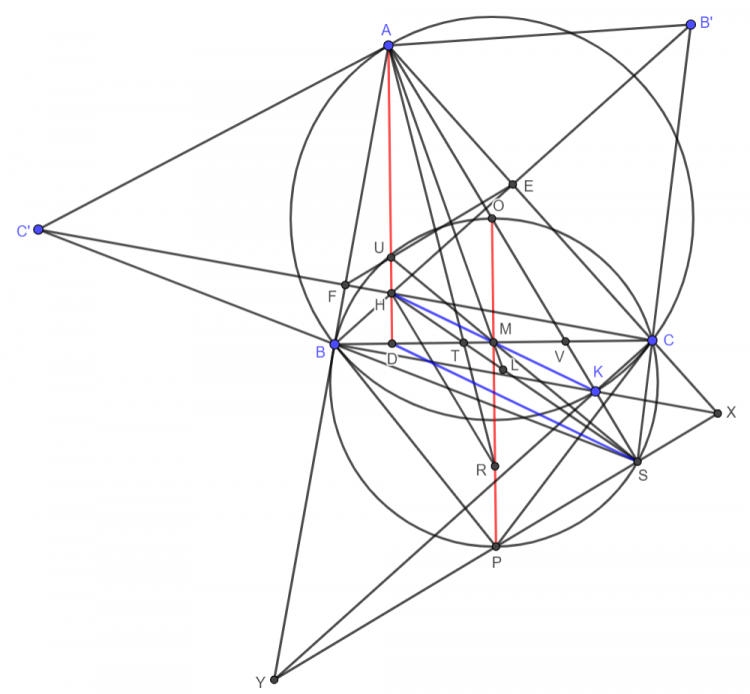
Từ ($1$) và ($2$) suy ra $\dfrac{AI}{IL}=\dfrac{DK}{DH}=\dfrac{RH}{DH}$. Theo bổ đề ERIQ đảo thì $AR,DL,IH$ đồng quy. Mà $\overline{I,H,O}$ theo bổ đề nên ta có đpcm. Bài toán đc giải quyết
Bài viết đã được chỉnh sửa nội dung bởi Dark Repulsor: 17-07-2021 - 09:47
![]()
![]()
![]()