Chủ đề này có 3 trả lời

[nhungvienkimcuong]

Đề thi Olympic Toán quốc tế năm 2023

Thời gian: 270 phút

 

Ngày thi thứ nhất: 08/07/2023

 

Bài 1. Xác định tất cả các hợp số $n>1$ thỏa mãn điều kiện sau: nếu $d_1,d_2, \dots, d_k$ là tất cả các ước nguyên dương của $n$ với $1=d_1<d_2<\dots<d_k=n$, thì $d_i$ là ước của $d_{i+1}+d_{i+2}$ với mọi $1\le i\le k-2$.

 

Bài 2. Cho tam giác nhọn $ABC$ với $AB<AC$. Gọi $\Omega$ là đường tròn ngoại tiếp của tam giác $ABC$. Gọi $S$ là điểm chính giữa cung $CB$ của $\Omega$ có chứa $A$. Đường thẳng vuông góc từ $A$ đến $BC$ cắt $BS$ tại $D$ và cắt lại $\Omega$ tại $E\neq A$. Đường thẳng qua $D$ song song với $BC$ cắt đường thẳng $BE$ tại $L$. Kí hiệu đường tròn ngoại tiếp của tam giác $BDL$ bởi $\omega$. Đường tròn $\omega$ cắt lại $\Omega$ tại $P\neq B$.

Chứng minh rằng đường tiếp tuyến của $\omega$ tại $P$ cắt đường thẳng $BS$ tại một điểm nằm trên đường phân giác trong của $\angle BAC$.

 

Bài 3. Với mỗi số nguyên $k\ge 2$, xác định tất cả các dãy vô hạn các số nguyên dương $a_1, a_2, \dots,$ để khi đó tồn tại một đa thức $P$ có dạng $P(x)=x^k+c_{k-1}x^{k-1}+\dots+c_1x+c_0$ với $c_0, c_1, \dots, c_{k-1}$ là các số nguyên không âm, sao cho

\[P(a_n)=a_{n+1}a_{n+2}\dots a_{n+k}\]

với mọi số nguyên $n\ge 1$.

 

 

Ngày thi thứ hai: 09/07/2023

 

Bài 4. Cho $x_1,x_2,\dots,x_{2023}$ là các số thực dương đôi một phân biệt sao cho

\[a_n=\sqrt{(x_1+x_2+\dots+x_n)\left(\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_n}\right)}\]

là một số nguyên với mọi $n=1,2,\dots,2023$. Chứng minh rằng $a_{2023}\ge 3034$.

 

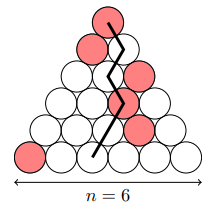
Bài 5. Cho $n$ là một số nguyên dương. Một tam giác Nhật Bản gồm $1+2+\dots+n$ hình tròn được xếp thành một hình tam giác đều sao cho với mỗi $i=1,2,\dots,n$, hàng thứ $i$ có đúng $i$ hình tròn và trên hàng đó có đúng một hình tròn được tô màu đỏ. Một đường đi ninja trong một tam giác Nhật Bản là một dãy gồm $n$ hình tròn nhận được bằng cách xuất phát từ hàng trên cùng, đi lần lượt từ một hình tròn xuống một trong hai hình tròn ngay dưới nó, và kết thúc tại hàng dưới cùng. Trong hình vẽ là một tam giác Nhật Bản với $n=6$ và một đường đi ninja có chứa hai hình tròn màu đỏ.

 Screenshot 2023-07-09 143751.png   15.42K   38 Số lần tải

Như một hàm số của $n$, tìm giá trị lớn nhất của $k$ sao cho trong mỗi tam giác Nhật Bản luôn có một đường đi ninja chứa ít nhất $k$ hình tròn màu đỏ.

 

Bài 6. Cho tam giác đều $ABC$. Các điểm $A_1,B_1,C_1$ nằm trong tam giác $ABC$ sao cho $BA_1=A_1C,CB_1=B_1A,AC_1=C_1B$ và

\[\angle BA_1C+\angle CB_1A+\angle AC_1B=480^{\circ}.\]

Cho $BC_1$ và $CB_1$ cắt nhau tại $A_2$, $CA_1$ và $AC_1$ cắt nhau tại $B_2$, $AB_1$ và $BA_1$ cắt nhau tại $C_2$.

Chứng minh rằng nếu $A_1B_1C_1$ là tam giác không cân thì các đường tròn ngoại tiếp của ba tam giác $AA_1A_2,BB_1B_2$ và $CC_1C_2$ sẽ đi qua hai điểm chung.

 

 

Nguồn: imo-official

Bài viết đã được chỉnh sửa nội dung bởi nhungvienkimcuong: 09-07-2023 - 12:39

[giappkk]

Bài $2$ ( hình ) đáp án của thầy Linh cũng khá chuẩn ạ. 

File gửi kèm

•  bai-2-imo-2023.pdf   122.42K   756 Số lần tải

[huytran08]

Câu 4 bất khá hay:

Đặt $m_{n}=x_{1}+x_{2}+...+x_{n},p_{n}=\frac{1}{x_{1}}+\frac{1}{x_{2}}+...+\frac{1}{x_{n}}$ thì $a_{n}= \sqrt{m_{n}.p_{n}}\in \mathbb{N}$ với mọi $n=1,2,...,2023$

Kết hợp với $AM-GM$ ta có biến đổi:

 $a_{n+1}^{2}=m_{n+1}.p_{n+1}=(m_{n}+x_{n+1})\left ( p_{n}+\frac{1}{x_{n+1}} \right )$

                                       

                                       $=m_{n}.p_{n}+\left ( \frac{m_{n}}{x_{n+1}}+p_{n}.x_{n+1} \right )+1$

 

                                       $=a_{n}^{2}+\left ( \frac{m_{n}}{x_{n+1}}+p_{n}.x_{n+1} \right )+1$

 

                                       $\geq a_{n}^{2}+2\sqrt{m_{n}.p_{n}}+1=a_{n}^{2}+2a_{n}+1=(a_{n}+1)^{2}$

 

 $\Rightarrow a_{n+1}\geq a_{n}+1$ với mọi $n$,dấu "$=$" xảy ra khi và chỉ khi $\frac{m_{n}}{x_{n+1}}=p_{n}.x_{n+1}$ hay $x_{n+1}^{2}=\frac{m_{n}}{p_{n}}$

 Giả sử tồn tại 2 giá trị $n_{o}$ và $n_{o}+1$ để dấu bằng xảy ra liên tiếp thì ta có:

 $x_{n_{o}+2}^{2}=\frac{m_{n_{o}+1}}{p_{n_{o}+1}}=\frac{m_{n_{o}}+x_{n_{o}+1}}{p_{n_{o}}+x_{n_{o}+1}}=\frac{m_{n_{o}}+\sqrt{\frac{m_{n_{o}}}{p_{n_{o}}}}}{p_{n_{o}}+\sqrt{\frac{m_{n_{o}}}{p_{n_{o}}}}}=\frac{m_{n_{o}}}{p_{n_{o}}}=x_{n_{o}+1}^{2}$

 Điều này mâu thuẫn vì $x_{1},x_{2},...,x_{2023}$ là các số thực dương đôi một phân biệt

Do đó $a_{n+2}\geq a_{n+1}+1\geq a_{n}+2$ suy ra $a_{n+2}\geq a_{n}+3 \forall n=1,2,...,2023 $ vì $a_{n}\in \mathbb{N}$(do $a_{n}\in \mathbb{Z}$ và $a_{n}>0$) và không xảy ra 2 dấu bằng liên tiếp.Từ đây ta có:

                                      $a_{2023}\geq a_{1}+3.1011\geq 3034$(đpcm)

Bài viết đã được chỉnh sửa nội dung bởi huytran08: 09-07-2023 - 22:16

[chuyenndu]

bài 1

gỉa sử n có nhiều hơn 2 ước nguyên tố, gọi 2 ước nguyên tố nhỏ nhất là p<q

thì $d_2=p$, tồn tại i sao cho $d_3=p^2,...,d_{i-1}=p^{i-2},d_i=q$

suy ra $d_{k-1}=\frac{n}{p},d_{k-2}=\frac{n}{p^2},\dots,d_{k-i+2}=\frac{n}{p^{i-2}},d_{k-i+1}=\frac{n}{q}$

$d_{k-i+1}|d_{k-i+2}+d_{k-i+3}\Rightarrow \frac{n}{q}|\frac{n}{p^{i-2}}+\frac{n}{p^{i-3}}\Rightarrow \frac{n}{q}|n+\frac{n}{p}\Rightarrow \frac{n}{p}|\frac{n}{q}\Rightarrow q|p$ (VL)

Bài viết đã được chỉnh sửa nội dung bởi chuyenndu: 10-07-2023 - 17:03