Chủ đề này có 10 trả lời

[thvn]

Để chào mừng diễn đàn trở lại, tôi xin gửi tới các bạn trẻ yêu bộ môn Hình Học sáng tác mới nhận được của thầy Nguyễn Bá Đang, bài toán như sau:

 

Cho tam giác ABC vuông tại A, các đường thẳng qua B và C đồng thời vuông góc với BC cắt CA tại E và AB tại D, M là trung điểm BC, H là hình chiếu của A trên BC, I là trung điểm AH.

Chứng minh rằng MI vuông góc DE.

[HaiDangPham]

Để chào mừng diễn đàn trở lại, tôi xin gửi tới các bạn trẻ yêu bộ môn Hình Học sáng tác mới nhận được của thầy Nguyễn Bá Đang, bài toán như sau:

 

Cho tam giác ABC vuông tại A, các đường thẳng qua B và C đồng thời vuông góc với BC cắt CA tại E và AB tại D, M là trung điểm BC, H là hình chiếu của A trên BC, I là trung điểm AH.

Chứng minh rằng MI vuông góc DE.

 

 

Một bài khó, mặc dù mới nhìn qua thì tưởng đơn giản. Cảm nhận ban đầu là mình có thể tìm ra 3 cách giải, nhưng sau mấy ngày suy nghĩ thì mới tìm được 1. 

 

Phương pháp tư duy của mình vẫn là thay vì tập trung nhiều vào kết luận, ta cố gắng mở rộng giả thiết, tức là thử nghiệm một cách tự do việc tạo ra các hình phụ từ đó rút ra các tính chất mới. Chính tiến trình này giúp mình nhìn ra hai đường phụ $BK$ và $BF$. Cuối cùng là ý tưởng sử dụng đường tròn. Đơn giản là mình đã nghĩ: "Tại sao không thử tạo ra đường tròn phụ?"  Và từ đây $MF$ và giao điểm $O$ với $AC$ được nhận ra dẫn đến điểm mấu chốt của toàn bộ lời giải là hai tam giác đồng dạng $DBG$ và $OMI$. 

 

 

LỜI GIẢI. Gọi $F$ là trung điểm $DC$. $MF$ cắt $AC$ tại $O$. Dễ thấy $MF$ là đường trung trực của $AC$ nên $MF$ vuông góc với $AC$, và $O$ là trung điểm của $AC$. Ngoài ra ta còn có ba điểm $B, I, F$ thẳng hàng. 

 

Tiếp theo kẻ $BK$ vuông góc $DE$, cắt $AE$ tại G. Tam giác $BDE$ có $G$ là trực tâm nên $DG$ vuông góc $BE$, từ đó suy ra $DG$ vuông góc $DC$. Ngoài ra, $OI$ là đường trung bình tam giác $AHC$ nên $OI$ song song $BC$, từ đó ta có $OI$ song song $DG$. 

 

Mục tiêu của chứng minh sau đây là chỉ ra hai tam giác $DBG$ và $OMI$ đồng dạng.

 

Hai tam giác này có ngay $\angle MOI=\angle BDG$. Lý do là bởi hai góc đó có hai cặp cạnh tương ứng song song. Như vậy ta chỉ còn phải chứng minh $$\frac{DG}{BD}=\frac{OI}{OM}$$ điều này tương đương $$\frac{DG}{BD}=\frac{HC}{AB}$$ bởi vì $OI=\frac{HC}{2}$ còn $OM=\frac{AB}{2}$. 

 

Bây giờ, dễ thấy hai tam giác $DGC$ và $HCA$ đồng dạng, suy ra $\frac{DG}{HC}=\frac{DC}{AH}$ Tam giác $BDC$ có $AH$ song song $CD$ nên theo Định lý Thales ta có $\frac{DC}{AH}=\frac{BD}{AB}.$ Suy ra $$\frac{DG}{HC}=\frac{BD}{AB}$$ và đây cũng chính là đẳng thức ta cần chứng minh ở trên. 

 

Như vậy ta đã chứng minh được hai tam giác $BDG$ và $MOI$ đồng dạng. Suy ra $$\angle OMI=\angle DBG=\angle OED$$ Vì vậy nếu gọi $S$ là giao điểm của $MI$ và $DE$ thì bốn điểm $S, O, M, E$ đồng viên, và do đó ta có ngay $MI$ vuông góc $DE$ tại $S$. 

Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 27-10-2023 - 08:13

[hovutenha]

Đây là cách sử dụng Định lí 4 điểm.

Ta có:

$IE^{2}=\frac{EA^{2}+EH^{2}}{2}-\frac{AH^{2}}{4}=\frac{EB^{2}-AB^{2}+EB^{2}+BH^2}{2}-\frac{AH^{2}}{4}=EB^{2}-\frac{3AH^{2}}{4}$

Tương tự:

$ID^{2}=DC^{2}-\frac{3AH^{2}}{4}$

Suy ra: 

$ID^{2}-IE^{2}=DC^{2}-EB^{2}=DM^{2}-EM^{2}$

Do đó: $IM$ vuông góc $ED$ (điều phải chứng minh)

[HaiDangPham]

 

Sau đây là cách giải thứ ba. 

 

Gọi $G$ là giao điểm của hai đường thẳng $DE$ và $BC$. $AH$ cắt $DE$ tại F. $AG$ cắt $BE$ tại $N$. Ta chứng minh không mấy khó khăn rằng $A$ là trung điểm của $FH$ và $N$ là trung điểm $BE$. 

 

Vì $MB=MA$ và $NB=NA$ nên hai tam giác $MBN$ và $MAN$ bằng nhau, suy ra $\angle MAN=\angle MBN=90^{\circ}$, hay $MA \perp AG$. 

 

Bây giờ, ta gọi $K$ là điểm đối xứng của $H$ qua $M$. Khi đó $MA$ là đường trung bình của tam giác $HFK$, vì thế ta có $AM \parallel FK$. Suy ra $AG \perp FK$. 

 

Tam giác $FKG$ có $AF \perp GK$, $AG \perp FK$ nên $A$ là trực tâm tam giác, dẫn tới $KA \perp FG$, nói cách khác ta có $KA \perp DE$.

 

Mà $IM \parallel KA$ (đường trung bình tam giác $KHA$), suy ra $MI \perp DE$. 

 

 

[HaiDangPham]

 

Sau cách giải thứ ba, mình có cảm giác về một cách giải nữa. Việc tìm ra không mấy khó khăn. Điểm mấu chốt nhất chính là nhìn ra ba điểm $E, M, K$ thẳng hàng. 

 

LỜI GIẢI. Không mất tính tổng quát ta giả sử $AB>AC$. Qua $B$ kẻ đường thẳng song song với $DE$ cắt đường thẳng $CD$ tại $F$. Đường thẳng $AH$ cắt $BE$ tại $K$. 

Trước hết, ta chứng minh $E, M, K$ thẳng hàng. Dễ thấy do $HK \parallel EB$ nên ta chỉ còn cần khẳng định được rằng $$\frac{MH}{MB}=\frac{HK}{BE}.$$ Thật vậy, lưu ý rằng $BFDE$ là hình bình hành nên $BE=DF$. Do đó $$\frac{HK}{EB}=\frac{AK-AH}{BE}=\frac{AK}{DF}-\frac{AH}{BE}.$$ Áp dụng liên tiếp Định lý Thales ta có $\frac{AK}{DF}=\frac{AB}{BD}=\frac{HB}{BC}$ và $\frac{AH}{BE}=\frac{HC}{BC}.$ Lưu ý giả thiết $AB>AC$ nên ta có $$\frac{HK}{BE}=\frac{HB}{BC}-\frac{HC}{BC}=\frac{(MH+MB)-(MC-MH)}{BC}=\frac{2MH}{BC}=\frac{MH}{MB}.$$ Vậy ta có $E, M, K$ thẳng hàng. 

 

Tiếp theo, ta thấy rằng tam giác $BAH$ và $ECB$ đồng dạng, mà $I$ là trung điểm $AH$, $M$ là trung điểm $BC$ nên không mấy khó khăn ta suy ra tam giác $BIH$ và $EMB$ cũng đồng dạng. Suy ra $\angle HBI=\angle BEM$.

 

Gọi $G$ là giao điểm của $BI$ và $EM$ khi đó dễ thấy $BI \perp EM$ tại $G$. Mà $E, M, K$ thẳng hàng nên $MK \perp BI$ tại $G$. 

 

Tam giác $BIK$ có $MK \perp BI$, $MB \perp IK$, vì vậy $M$ là trực tâm tam giác, dẫn tới $MI \perp BK$. Mà $BK \parallel DE$ nên ta có $MI \perp DE$. 

Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 28-10-2023 - 23:07

[HaiDangPham]

Cách giải cuối cùng. Phức tạp hơn cả, nhưng cũng đáng để tìm kiếm. Cảm giác rất thú vị. 

 

LỜI GIẢI. Gọi $G$ là điểm đối xứng với $B$ qua $I$. $AH$ lần lượt cắt $DE, GC$ tại $K, N$. $DE$ và $BC$ cắt nhau tại $F$. $J$ là trung điểm $CD$. 

 

Ta lần lượt xét các mệnh đề. 

 

Mệnh đề 1. $IM \parallel NG$. 

 

Đúng vì $IM$ là đường trung bình của tam giác $BCG$. 

 

Mệnh đề 2. $B, I, J$ thẳng hàng; $A, J, F$ thẳng hàng. 

 

Đây là bài toán cơ bản, mình tạm lược bỏ chứng minh. 

 

Mệnh đề 3. $EM \perp BI$. 

 

Tam giác BCE đồng dạng tam giác $HAB$, hơn nữa, $M$ là trung điểm $BC$, $I$ là trung điểm $AH$ nên ta suy ra tam giác $BHI$ đồng dạng tam giác $EBM$. Từ đó có $\angle BEM=\angle IBH$, và suy ra $IB \perp EM$.

 

Mệnh đề 4. $KC \parallel EM$.

 

Tiếp theo, ta có $\frac{KF}{KE}=\frac{KF}{KD}.\frac{KD}{KE}$ . Trong đó $\frac{KF}{KD} =\frac{HF}{HC}$ (tam giác $HKF$ có $CD \parallel KH$), còn $\frac{KD}{KE}=\frac{HC}{HB}$ (hình thang $BCDE$ có $KH$ song song hai đáy $CD, BE$). Vì vậy $$\frac{KF}{KE}=\frac{HF}{HC}.\frac{HC}{HB}=\frac{HF}{HB}$$ điều này chứng tỏ $KC \parallel EM$. 

 

Mệnh đề 5. $AM \perp AF$ và $AM^2=MH.MF$. 

 

Vì $A, J, F$ thẳng hàng (Mệnh đề 2) và $J$ là trung điểm $CD$ nên $\angle FAC=\angle JAC=\angle JCA=\angle MBA=\angle MAB$. Từ đó suy ra $\angle FAC+\angle MAC=\angle MAB+\angle MAC=90^{\circ}$. Vậy $AM \perp AF$. 

Tam giác $MAF$ vuông tại $A$ và có $AH \perp MF$, theo hệ thức lượng trong tam giác ta có $AM^2=MH.MF$. 

 

Mệnh đề 6. $BG \parallel FN$. 

 

Vi $MA=MC, JA=JC$ nên $JM$ là đường trung trực của $AC$, dẫn tới $JM \perp AC$, suy ra $JM \parallel AB$. Theo định lý Thales ta có $$\frac{AJ}{JF}=\frac{MB}{MF}=\frac{BC}{2MF}$$ Ta lại có $IM \parallel NG$ (Mệnh đề 1) suy ra $$\frac{IA}{IN}=\frac{IH}{IN}=\frac{MH}{MC}=\frac{2MH}{BC}.$$ Theo Mệnh đề 5, ta có $AM^2=MH.MF$ hay $$\frac{BC}{2MF}=\frac{2MH}{BC}$$ Do đó $\frac{AJ}{JF}=\frac{IA}{IN}$. Nói cách khác $IJ \parallel NF$. Mà $B, I, J$ thẳng hàng (Mệnh đề 2) nên $NF \parallel BG$. 

 

Mệnh đề 7. $MI \perp DE$. 

 

Theo Mệnh đề 3 và Mệnh đề 4 ta suy ra $KC \perp BG$. Mà theo Mệnh đề 6 ta có $BG \parallel NF$ nên $KC \perp NF$. 

Tam giác $KNF$ có $KC \perp NF$, $FH \perp NK$, suy ra $C$ là trực tâm tam giác. Do đó $NG \perp KF$ hay $NG \perp DE$. 

Cuối cùng, theo Mệnh đề 1, $MI \parallel NG$ nên $MI \perp DE$. 

Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 31-10-2023 - 12:38

[HaiDangPham]

Thêm một cách giải nữa...Cảm giác thôi thúc để đi tìm kiếm một cái gì còn dang dở.

 

Các cách giải trước của mình chủ yếu sử dụng Định Lý Thales và tính chất ba đường cao đồng quy trong tam giác. Cách giải sau đây ngoài hai lý thuyết trên còn vận dụng thêm Hệ thức lượng trong tam giác vuông và Định lý Menelaus.

 

Cách giải gồm hai ý tưởng chính làm điểm xuất phát. Thứ nhất, đường thẳng qua $M$ song song với $DE$. Thứ hai, hình chữ nhật chứa ba đỉnh $B, C, E$ từ đó sinh ra trung điểm $EC$. Cả hai ý tưởng này đều được thấy bởi trực giác. Không có một phương pháp nào ở đây cả. Chúng xuất hiện và mình đi theo chúng. 

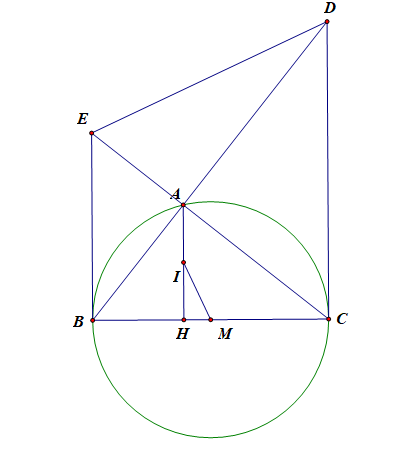
LỜI GIẢI.  Cần thêm các điểm phụ như sau:

• Qua $M$ kẻ đường thẳng song song với $DE$ cắt $BE$ tại $N$
• Lấy $P$ là trung điểm $EC$
• $MP$ cắt $AB$ tại $K$
• Lấy $Q$ là trung điểm $CD$ 
• $QK$ cắt $AC$ tại $G$
• $DE$ và $BC$ kéo dài cắt nhau tại $F$. 

Mệnh đề 1. $A, Q, F$ thẳng hàng và $AF \perp AM$.  

 

Chứng minh $A, Q, F$ thẳng hàng là một bài toán cơ bản; chứng minh không phải quá dễ, nhưng mình vẫn xin được lược bỏ để tập trung vào các lập luận chính yếu hơn. Ý tưởng chính: gọi giao điểm $AH$ và $DE$ là $H'$ khi đó $A$ là trung điểm $HH'$. 

 

Có $A, Q, F$ thẳng hàng rồi thì dễ dàng suy ra $AF \perp AM$. Chứng minh điều này tham khảo cách giải trước của mình. 

 

Mệnh đề 2. $MA^2=MH.MF$. 

 

Theo Mệnh đề 1 ta có $AM \perp AF$, nên tam giác $AMF$ vuông tại $A$ và có đường cao $AH$. Theo hệ thức lượng trong tam giác ta có $MA^2=MH.MF$. 

 

Mệnh đề 3. $PQ$ song song $DE$. 

 

Ta có $MA=MC, QA=QC$ nên $MQ$ là đường trung trực của $AC$. Do đó $MQ \perp AC$, dẫn tới $MQ \parallel AB$. Suy ra $\frac{FQ}{AQ}=\frac{MF}{MB}$.

 

Ta có $MP$ là đường trung bình của tam giác $BEC$ nên $MP \parallel BE$. Trong hình thang $BEAH$ ta có $\frac{EP}{AP}=\frac{MB}{MH}$. 

 

Bây giờ, theo Mệnh đề 2, ta có $MA^2=MH.MF$ mà $MA=MB$ nên $MB^2=MH.MF$ hay $\frac{MB}{MH}=\frac{MF}{MB}$. 

 

Vậy ta có $\frac{FQ}{AQ}=\frac{EP}{AP}$. Theo định lý Thales ta suy ra $PQ \parallel EF$ hay $PQ \parallel DE$.  

 

Mệnh đề 4. $M, I, G$ thẳng hàng. 

 

Do $MP \parallel BE$ nên $MP \parallel CD$, mà $M$ là trung điểm $BC$ dẫn tới $K$ là trung điểm $BD$. Tam giác $BDC$ có $QK$ là đường trung bình nên $QK \parallel BC$ hay $QG \parallel CF$. 

 

Theo Mệnh đề 1 ta có $A, Q, F$ thẳng hàng. Ngoài ra, do $QG \parallel CF$, áp dụng định lý Thales trong tam giác $ACF$ ta có $\frac{AG}{CG}=\frac{AQ}{FQ}=\frac{MB}{MF}$. Ta lại có theo Mệnh đề 2, do $MA=MB=MC$ nên $MB.MC=MH.MF$, nói cách khác  $\frac{MB}{MF}=\frac{MH}{MC}.$ Vì vậy $\frac{AG}{CG}=\frac{MH}{MC}$. 

 

Trong tam giác $AHC$ xét ba điểm $M, I, G$ có $\frac{AG}{CG}.\frac{MC}{MH}.\frac{IH}{IA}=1$. Theo định lý Menelaus ta có $M, I, G$ thẳng hàng. 

 

Mệnh đề 5. $MI$ vuông góc $DE$. 

 

Ta có $QK \parallel BC$ nên $QK \perp MP$. Hơn nữa, $PG \perp QM$. Chứng tỏ $G$ là trực tâm tam giác $MPQ$. Suy ra $MG \perp PQ$. 

 

Ta lại có $M, I, G$ thẳng hàng (Mệnh đề 4) nên $MI \perp PQ$. Hơn nữa, $PQ \parallel DE$ (Mệnh đề 3) nên $MI \perp DE$. 

Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 02-11-2023 - 15:47

[HaiDangPham]

Một lời giải khác nữa, gần tương tự cách giải số 4. Điểm cốt lõi của hai cách giải là sử dụng một bổ đề về hai tam giác đồng dạng. 

 

Bổ đề. Cho tam giác $ABC$ và tam giác $A'B'C'$ đồng dạng. $M, M'$ là hai điểm lần lượt thuộc $BC, B'C'$ sao cho $\frac{MB}{MC}=\frac{M'B'}{M'C'}$. Khi đó tam giác $AMB$ đồng dạng tam giác $A'M'B'$ và tam giác $AMC$ đồng dạng tam giác $A'M'C'$.

 

Cùng với Định lý Thales, bổ đề này thật sự quan trọng. Chứng minh thì khá đơn giản, xin dành cho bạn đọc. 

 

Bây giờ quay trở lại bài toán ban đầu với cách giải thứ 7. Với mình, đây là cách giải đơn giản và đẹp nhất. 

LỜI GIẢI. Gọi $K$ là trung điểm $CD$. Hai đường thẳng $BC, DE$ cắt nhau tại $F$. $N$ là trung điểm $HF$. 

 

Ta có  $B, I, K$ thẳng hàng; $A, K, F$ thẳng hàng và $AF \perp AM$. 

 

Tam giác $MAH$ và tam giác $AFH$ đồng dạng. $I, N$ tương ứng là trung điểm $AH, FH$. Theo bổ đề đã nói, ta có tam giác $MAI$ đồng dạng tam giác $AFN$. Suy ra $\angle AMI=\angle FAN$, dẫn tới $MI \perp AN$. 

 

Tiếp theo, $IN$ là đường trung bình tam giác $HAF$ nên $IN \parallel AF$. Do $A, K, F$ thẳng hàng nên $IN \parallel KF$.

 

Mặt khác do $B, I, K$ thẳng hàng, $IH \parallel KC$, trong tam giác $BKF$ ta có $\frac{BN}{FN}=\frac{BI}{KI}$. Trong tam giác $BDC$ ta có $AH \parallel CD$ nên $\frac{BI}{KI}=\frac{BA}{DA}$.

 

Do vậy $\frac{BN}{FN}=\frac{BA}{DA}$.

 

Chứng tỏ $AN \parallel FD$ hay $AN \parallel DE$. Mà $MI \perp AN$ theo chứng minh trên nên $MI \perp DE$. 

Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 03-11-2023 - 04:37

[thvn]

Cảm ơn bạn HaiDangPham , một người thầy rất đam mê hình học!

Học sinh được nhờ lắm đấy     

[HaiDangPham]

Cảm ơn bạn HaiDangPham , một người thầy rất đam mê hình học!

Học sinh được nhờ lắm đấy     

 

Dạ, em cảm ơn thầy đã khen ngợi ạ! 

Các bài toán của Thầy Nguyễn Bá Đang quả thật rất hấp dẫn. Gần như bài nào Thầy đăng lên em cũng thích thú và tìm được nhiều cách giải. Cảm ơn sự chia sẻ của các Thầy ạ!

[thvn]

Dạ, em cảm ơn thầy đã khen ngợi ạ! 

Các bài toán của Thầy Nguyễn Bá Đang quả thật rất hấp dẫn. Gần như bài nào Thầy đăng lên em cũng thích thú và tìm được nhiều cách giải. Cảm ơn sự chia sẻ của các Thầy ạ!

    chúc bạn một tuần mới vui vẻ!