Chủ đề này có 2 trả lời

[MHN]

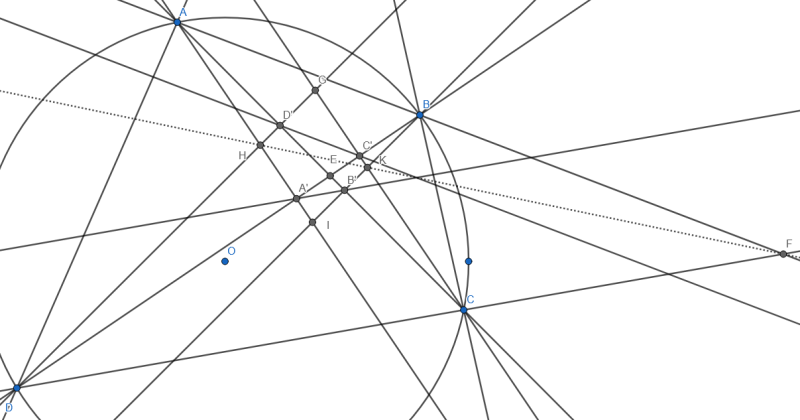
Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$; $AC$ cắt $BD$ tại $E$; $AB$ cắt $CD$ tại $F$. Các đường cao $AA';DD'$ của $\Delta EAD$ cắt nhau tại $H$, các đường cao $BB';CC'$ của $\Delta EBC$ cắt nhau tại $K$. Chứng minh rằng: $F;H;K$ thẳng hàng.

[perfectstrong]

 

Bài này đẹp nhỉ Nếu dùng kiến thức cấp 3 thì $F,H,K$ cùng nằm trên trục đẳng phương của 2 đường tròn đường kính $AB$ và $CD$. Còn dùng cấp 2 thì chưa biết sao

[perfectstrong]

Một cách "trâu bò" theo cấp 2 (vắn tắt):

Vẽ $DH$ cắt $CK$ tại $G$, $AH$ cắt $BK$ tại $I$. Dễ thấy $GHIK$ là hình bình hành.

Ta sẽ chứng minh bằng Menelaus đảo cho tam giác $GDC$ với cát tuyến $H,K,F$:

\begin{equation}\label{eq_target} \frac{{HD}}{{HG}}\frac{{KG}}{{KC}}\frac{{FC}}{{FD}} = 1\end{equation}

Trước hết, ta sẽ tính từng tỉ số một, chú ý các cặp song song: $DD' \parallel BB'$ và $AA' \parallel CC'$.

\begin{equation}\label{eq_frac_1}\frac{{HD}}{{HG}} = \frac{{A'D}}{{A'C'}}\end{equation}

\begin{equation}\label{eq_frac_2} \frac{{KG}}{{KC}} = \frac{{B'D'}}{{B'C}}\end{equation}

Vậy từ \eqref{eq_frac_1} và \eqref{eq_frac_2}, ta có được:

\begin{equation}\label{eq_frac_1_2} \frac{{HD}}{{HG}}\frac{{KG}}{{KC}} = \frac{{A'D}}{{A'C'}}\frac{{B'D'}}{{B'C}} = \frac{{A'D}}{{B'C}}\frac{{B'D'}}{{A'C'}} \end{equation}

Tiếp tục tìm cách xử lý từng tỉ số:

\[\frac{{ED'}}{{ED}} = \frac{{EB'}}{{EB}} = \frac{{ED' + EB'}}{{ED + EB}} = \frac{{B'D'}}{{BD}} \Rightarrow B'D' = BD\frac{{ED'}}{{ED}}\]

Tương tự, ta có $A'C' = AC\frac{{EA'}}{{EA}}$ nên $\frac{{B'D'}}{{A'C'}} = \frac{{BD}}{{AC}}\frac{{ED'}}{{ED}}\frac{{EA}}{{EA'}} = \frac{{BD}}{{AC}}$ (chú ý rằng $\Delta EAA' \sim \Delta EDD' \Rightarrow ED'.EA = EA'.ED$)

Lại có $A'B'\parallel CD \Rightarrow \frac{{A'D}}{{B'C}} = \frac{{EA'}}{{EB'}} = \frac{{ED}}{{EC}} = \frac{{AD}}{{BC}}$ (do $\Delta EDA \sim \Delta ECB$)

Từ \eqref{eq_frac_1_2}, ta có được \[\frac{{HD}}{{HG}}\frac{{KG}}{{KC}} = \frac{{AD}}{{BC}}\frac{{BD}}{{AC}}\]

Vậy để có \eqref{eq_target}, ta chỉ cần cm \[\frac{{FD}}{{FC}} = \frac{{AD}}{{BC}}\frac{{BD}}{{AC}}\]

Mà điều này thì chỉ cần sử dụng $\Delta FCB \sim \Delta FAD$  và $\Delta FBD \sim \Delta FCA$. Ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 27-03-2024 - 17:23
Rút gọn