Chủ đề này có 2 trả lời

[thinhsuperpro]

cho góc $xOy$ cố định và điểm $A$ cố định trên $Ox$. Đường tròn $(I)$ thay đổi nhưng luôn tiếp xúc với $Ox, Oy$ tại $E$ và $D$. Gọi $AF$ là tiếp tuyến thứ hai kẻ từ $A$ tới $(I)$. Cmr $DF$ luôn đi qua 1 điểm cố định.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 27-03-2024 - 17:08
LaTeX

[William Nguyen]

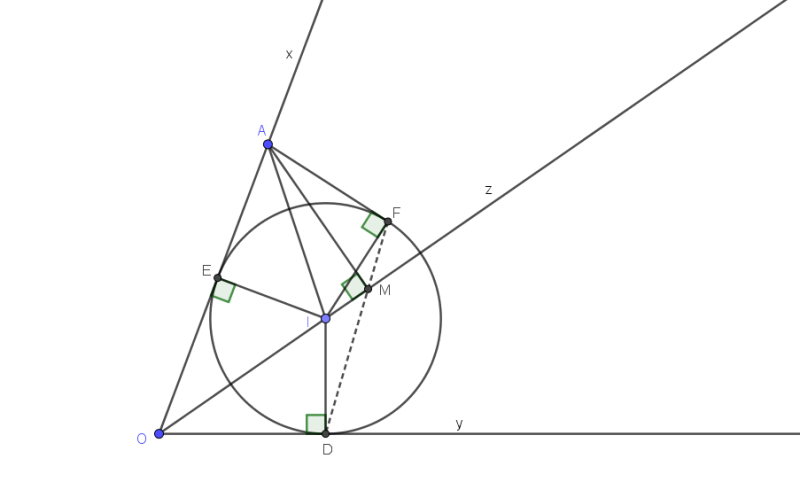
Đường tròn tâm $I$ luôn tiếp xúc hai tia $Ox, Oy$ nên $I$ di chuyển trên tia phân giác $Oz$ của góc $xOy$, trừ điểm $I$.

 

Gọi $M$ là chân đường vuông góc hạ từ $A$ xuống $Oz$ thì thấy $DF$ đi qua $M$, chính là điểm cố định cần tìm. Ta sẽ chứng minh $DF$ luôn đi qua $M$.

 

Xét lần lượt các vị trí của $I$ từ gần đến xa $O$:

 

TH1: $OI<OM, AE>AM$

4 điểm $A,E,I,F,M$ thuộc đường tròn đường kính $AI$.

Ta có $OI.OM=OE.OA=OD.OA \Rightarrow \frac{OD}{OM}=\frac{OI}{OA}$ nên $\bigtriangleup ODM \sim \bigtriangleup OIA$ $(c.g.c)$ $(1)$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{EAI}=\widehat{FAI}=\widehat{OMF}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH2: $OI<OM, AE=AM$ thì $F$ trùng $M$

 

 

TH3: $OI<OM, AE<AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{FAI}=\widehat{FMz}$

Vậy $D, M, F$ thẳng hàng.

 

 

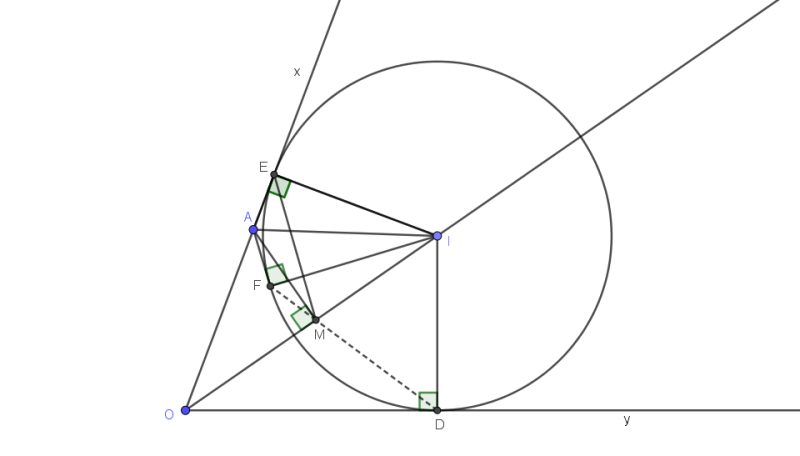
TH4: $I$ trùng $M$

Có $\widehat{AIE}=\widehat{AIF}, \widehat{EIO}=\widehat{DIO}$

Mà $\widehat{AIE}+\widehat{EIO}=\widehat{AIO}=90^{\circ}$

nên $\widehat{AIE}+\widehat{AIF}+\widehat{EIO}+\widehat{DIO}=180^{\circ}$ hay $F, I, D$ thẳng hàng.

Vậy $D, M, F$ thẳng hàng.

 

 

TH5: $OI>OM, OE<OA$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI}=\widehat{FAI}=\widehat{FMI}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH6: $OI>OM, OE>OA, AE<AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI} \Rightarrow \widehat{IMD}=\widehat{EAI}=90^{\circ}-\widehat{EIA}=90^{\circ}-\widehat{FIA}=90^{\circ}-\widehat{FMA}$

$\Rightarrow \widehat{IMD}+\widehat{FMA}=90^{\circ}$

Vậy $D, M, F$ thẳng hàng.

 

 

TH7: $OI>OM, AE=AM$ thì $F$ trùng $M$

 

 

TH8: $OI>OM, OE>OA, AE>AM$

Từ $(1) \Rightarrow \widehat{OMD}=\widehat{OAI} \Rightarrow \widehat{IMD}=\widehat{EAI}=\widehat{FAI}=\widehat{EAI}=\widehat{IMF}$

Vậy $D, M, F$ thẳng hàng.

 

 

Kết thúc bài toán.

[perfectstrong]

Lời giải rất cẩn trọng và đáng nể Bởi thế mới thấy nếu sử dụng góc định hướng thì cả 7 TH đều quy về 1