Anh em xem giúp 1001001 với. Vừa rồi thi có bài BĐT dễ ẹt chỉ cần nhân tung lên rồi chơi Murihead là ra vậy mà mình cứ đi lòng vòng mới chuối chứ!

Khi đứng trước 1 bài BĐT bạn sẽ làm gì?
Started By 1001001, 30-11-2006 - 06:13
#1
 Posted 30-11-2006 - 06:13
Posted 30-11-2006 - 06:13

My major is CS.
#2
 Posted 07-01-2007 - 14:52
Posted 07-01-2007 - 14:52

Tôi nghĩ bạn không cần lo lắng về ch đó đâu. Ch này la bình thường đối với ~ người hoc toán mà. Cho hỏi tí; cái bài bạn nói nó thế nào vậy. Post lên cho anh em cùng tham khảo được hok?

[URL=http://animegifs.free.fr/games/streetfighter/page5/streetfighter-17.gif]

#3
 Posted 09-01-2007 - 23:00
Posted 09-01-2007 - 23:00

BĐT Muirhead phát biểu thế nào vậy  , mình nghe tên rồi nhưng chưa biết mặt
, mình nghe tên rồi nhưng chưa biết mặt 
#4
 Posted 20-03-2007 - 23:06
Posted 20-03-2007 - 23:06

đại loại là cho a1, b1,a2,b2,a3,b3 là các số thực và a1  a2
a2 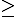 a3 và b1
a3 và b1  b2
b2 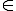 b3. a1 + a2
b3. a1 + a2 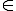 b1+b2, a1 + a2 + a3 = b1 + b2 + b3
b1+b2, a1 + a2 + a3 = b1 + b2 + b3
Cho x,y,z là các số thực dương, ta có sym (x^a1)(y^a2)(z^a3)
sym (x^a1)(y^a2)(z^a3) 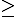
 sym (x^b1)(y^b2)(z^b3)
sym (x^b1)(y^b2)(z^b3)
Trong cuốn Topics in Inequalities - Theorems and Techniques của Hojoo Lee ( search google cái tên sách ra ngay file pdf ) có nói về bđt này
) có nói về bđt này  .
.
Cho x,y,z là các số thực dương, ta có
Trong cuốn Topics in Inequalities - Theorems and Techniques của Hojoo Lee ( search google cái tên sách ra ngay file pdf
Edited by JokySpy, 20-03-2007 - 23:07.
xin đc bắt đầu sự nghiệp bằng việc chăn bài gà... =))
#5
 Posted 07-03-2011 - 10:50
Posted 07-03-2011 - 10:50

đại loại là cho a1, b1,a2,b2,a3,b3 là các số thực và a1
a2
a3 và b1
b2
b3. a1 + a2
b1+b2, a1 + a2 + a3 = b1 + b2 + b3
Cho x,y,z là các số thực dương, ta cósym (x^a1)(y^a2)(z^a3)
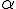
sym (x^b1)(y^b2)(z^b3)
Trong cuốn Topics in Inequalities - Theorems and Techniques của Hojoo Lee ( search google cái tên sách ra ngay file pdf) có nói về bđt này
.
mình cũng nghe danh muiheard từ lâu mà chưa bik mặt, sao trông gần giống Karamata vậy
#6
 Posted 07-03-2011 - 11:42
Posted 07-03-2011 - 11:42

mình cũng nghe danh muiheard từ lâu mà chưa bik mặt, sao trông gần giống Karamata vậy
Cũng tùy dạng thôi, nếu cho tổng thì khác mà cho tích thì hướng nó sẽ khác! Nhưng dạo này đề thi DH toàn cho dạng hàm số! Lắm khi cũng thấy chán!
"Phong độ là nhất thời, đẳng cấp là mãi mãi"!!!
#7
 Posted 07-03-2011 - 17:15
Posted 07-03-2011 - 17:15

sặc... các bạn ko đánh giá xem nó thuộc cấu hình nào và đang thi ở kỳ thi nào à? Chẳng nhẽ bài nào cũng vác đao to búa
lớn mà phá nó chắc gì đã ra..... mỗi pp cm BDT đều có ưu điểm riêng. Chẳng có cái nào là bài nào cũng áp dụng được...
Trong mỗi cấu hình cần có thủ thuật riêng... biết nhiều BDT là tốt nhưng chưa chắc đã có lợi nếu chưa gì đã cắm đầu cắm cổ
vào chém.
p/s: Tôi có biết 1 anh học trước tôi 3 khóa ở lớp học BDT rất kém nhưng đi thi thì bài BDT nào cũng làm được (kể cả bài
VNTST 2009-chỉ vài người làm đươc).
lớn mà phá nó chắc gì đã ra..... mỗi pp cm BDT đều có ưu điểm riêng. Chẳng có cái nào là bài nào cũng áp dụng được...
Trong mỗi cấu hình cần có thủ thuật riêng... biết nhiều BDT là tốt nhưng chưa chắc đã có lợi nếu chưa gì đã cắm đầu cắm cổ
vào chém.
p/s: Tôi có biết 1 anh học trước tôi 3 khóa ở lớp học BDT rất kém nhưng đi thi thì bài BDT nào cũng làm được (kể cả bài
VNTST 2009-chỉ vài người làm đươc).
#8
 Posted 28-06-2011 - 13:46
Posted 28-06-2011 - 13:46

Trong quyển kim cương có đầy đủ mà
1 user(s) are reading this topic
0 members, 1 guests, 0 anonymous users






