Bài 1: Giài hệ phương trình:
$\left{\begin{2(x^3 - y^3) - x(x+1)(x-2) =1}\\{2(y^3 - z^3) - y(y+1)(y-2) =1}\\{2(z^3 -x^3) - z(z+1)(z-2) =1}$
Bài 2: Cho 3 số thực dương a,b,c thỏa : $\ a+b+c\geq\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}$
c/m: $\ a+b+c\geq \dfrac{3}{a+b+c} + \dfrac{2}{abc} $
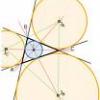
Bài 3:Cho tam giác ABC vuông tại A. Dlà điểm di động trên cạnh AC. Đường tròn (O) đường kính BDcắt BC tại điểm thứ hai là P. Đường cao vẽ từ A cùa tam giác ABD cắt (O) tại điểm thứ hai là E. Gọi F là giao điểm của CE và DP. I là giao điểm của AF và DE. Đường thẳng qua I song song DP cắt đường trung trực AI tại M. C/m M di động trên 1 đường cố định khi D di động trên AC.
Bài 4:
Cho tứ diện ABCD nội tiếp mặt cầu tâm O. MẶt phẳng (Q) vuộng góc OA, cắt AB,AC,AD tại M,N,P. c/m B,C,D,M,N,P cùng thuộc 1 mặt cầu.
Bài 5:Tìm tất cả các hàm f: R-> R thoả:
f(x-f(y)) = f(f(y)) + xf(y) + f(x) -1 , với mọi x,y thuộc R
BÀi 6: Cho số thực x,y,z thỏa :
$\left{\begin{x\ge y \ge z \ge 1}\\{2y + 3z \ge 6}\\{11x+27z \ge 54}$
Tìm giá trị lớn nhất P(x,y,z)= $\dfrac{1}{x^2} + \dfrac{2008}{y^2} + \dfrac{2009}{z^2}$
Bài 7: Cho đa thức $P_k (x) =1 - x + x^2 - x^3 + ... + (-1)^{k-1} x^{k-1}$ , k nguyên dương
c/m: $\sum_{k=1}^n C_n^k P_k (x)= 2^{n-1} P_n (\dfrac{x-1}{2} )$
Bài viết đã được chỉnh sửa nội dung bởi mai quoc thang: 28-11-2008 - 20:54