Một tờ giấy có dạng hình vuông $ABCD$. Gấp tờ giấy sao cho $C$ nằm trên cạnh $AB$. Tìm giá trị nhỏ nhất của $\dfrac{MR}{RQ}$
...đề cho giấy $ABCD$, mà sao hình vẽ lại là $ABDC$ ?
~~~~
...Theo hình vẽ:
Cách khác vậy ^^~
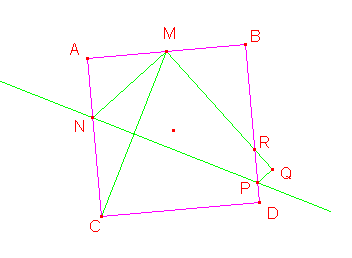
-Chọn hệ tọa độ trực chuẩn nhận độ dài cạnh hình vuông làm đơn vị sao cho:
$C=0+0.i$, $A=0+i$, $B=1+i$, $D=1+0.i$
-Điểm $M$ nằm trên cạnh $AB$: $M=k+i$ ( Với $k\in [0;1]$ )
-Để tạo điểm $Q$, ta tiến hành như sau: Thực hiện phép quay 'động' quanh $C$ để cố định $M$ tại điểm $(0+i)$, lấy đối xứng điểm $D$ qua đường thẳng $Im(z)=0,5$ và trả lại ảnh ban đầu :
Thể hiện qua hàm chuyển ảnh :
$Q=w(D)=\left( i+cọnjugate(\frac{i}{M} .D ) \right)\frac{M}{i}=M-\frac{M}{\bar{M}}=M-\frac{M^2}{|M|^2}$
-Do $M,R,Q$ thẳng hàng, theo Thales, ta có:
$\frac{MR}{RQ}=\left| \frac{M-R}{R-Q} \right|=\left| \frac{Re(M-1)}{Re(Q-1)} \right|=\left| \frac{k-1}{k-1-\frac{k^2-1}{k^2+1}} \right|=\left| \frac{k^2+1}{k(k-1)} \right|=\frac{k^2+1}{k(1-k)}=f(k)$
$\Rightarrow f'(k)=\frac{k^2+2k-1}{k^2(1-k)^2}=0\Leftrightarrow k=\pm \sqrt{2}-1$
Theo đó: $min\frac{MR}{RQ} =\min_{k\in [0;1]}f(k)=min(\lim_{k\rightarrow 0} f(k), f(\sqrt{2}-1),\lim_{k\rightarrow 1} f(k))=f(\sqrt{2}-1)=2+2\sqrt{2}$
-Giá trị đạt tại $k=\sqrt{2}-1$, hay $AM=(\sqrt{2}-1) a$ ( Với $a$ là độ dài cạnh hình vuông )
Bài viết đã được chỉnh sửa nội dung bởi robin997: 20-02-2013 - 02:35







