Câu 1:
Cho $ A=\dfrac{\sqrt{x-1-2\sqrt{x-2}}}{\sqrt{x-2}-1} $
1. Tìm điều kiện của x
2. Tính $ A^2 $
3. Rút gọn A
Câu 2:
Cho phân thức: $ P=\dfrac{n^{3}+2n^{2}-1}{n^{3}+2n^{2}+2n+1} $
a. Rút gọn P
b. Chứng minh: Nếu n là số nguyên thì kết quả tìm đc là phân sô tối giản
ps:Còn 3 câu nữa xí hồi up tiếp.

Đề thi chọn HSG lớp 9 THCS Quảng Trị (2009-2010)
Bắt đầu bởi hoangnamfc, 02-03-2010 - 13:39
#1
 Đã gửi 02-03-2010 - 13:39
Đã gửi 02-03-2010 - 13:39

#2
 Đã gửi 02-03-2010 - 14:37
Đã gửi 02-03-2010 - 14:37

anh post nhanh lên mấy bài rút gọn này thì ai mà chả làm được.
Give me some sunshine
Give me some rain
Give me another chance
I wanna grow up once again
Give me some rain
Give me another chance
I wanna grow up once again
#3
 Đã gửi 02-03-2010 - 15:15
Đã gửi 02-03-2010 - 15:15

Thế là đề HSG đó em.anh post nhanh lên mấy bài rút gọn này thì ai mà chả làm được.
Bài 2 áp dụng tính chất 2 số lẻ liên tiếp
Tiếp tục 3 bài còn lại
Câu 3:
1. Giải hệ
$\left\{ \begin{gathered} \left\{ {x - y = \left( {\sqrt y - \sqrt x } \right)} \right.\left( {1 + xy} \right) \hfill \\ x^3 + y^3 = 54 \hfill \\ \end{gathered} \right. $
2. Cho a,b,c>0; Chứng minh
$ \dfrac{{a^3 + b^3 }}{{2ab}} + \dfrac{{b^3 + c^3 }}{{2bc}} + \dfrac{{a^3 + c^3 }}{{2ac}} \geqslant a + b + c $
Câu 4.
câu a dễ khỏi ghi
câu b:
Tìm x,y thỏa mãn
$ x^3 = y^3 + 2\left( {x^2 + y^2 } \right) + 3xy + 17 $
Câu 5:
1. Cho tam giác ABC có $ \widehatA = 60^0 $. Chứng minh
$ BC^2 = AB^2 + AC^2 - AB.AC $
2. Cho tam giác đều ABC. Gọi D là điểm đối xứng của B qua đường thẳng AC. ĐƯờng thằng qua B cắt các tia AD, DC tại M và N. AN và CM cắt nhau tại E.
Chứng mình.
A,C,D,E cùng năm trên 1 đường tròn
#4
 Đã gửi 05-03-2010 - 21:23
Đã gửi 05-03-2010 - 21:23

câu 2 bạn nhớ poss thêm câu a> để làm đủ hơn nha

#5
 Đã gửi 05-03-2010 - 22:10
Đã gửi 05-03-2010 - 22:10

Là câu 4 chứ nhưng câu này câi a ko liên quan câu b.câu 2 bạn nhớ poss thêm câu a> để làm đủ hơn nha
#6
 Đã gửi 05-03-2010 - 22:32
Đã gửi 05-03-2010 - 22:32

Mình xin phần 2 câu dễ trước!
Câu 3)
a) Giải hệ
Đk: x,y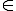 0
0  xy+1>0
xy+1>0
Xét PT $ x-y=(sqrt{y}-sqrt{x})(1+xy)$
Nếu x>y thì VT>0, VP <0 pt vô nghiệm
pt vô nghiệm
Nếu x<y thì VT<0 VP>0 pt vô nghiệm
pt vô nghiệm
 x=y thay vào pt (2)
x=y thay vào pt (2)
 $ 2x^3=54 $
$ 2x^3=54 $  x=3
x=3
Vậy PT có nghiệm x=y=3.
b) Chứng minh bdt
$ \dfrac{a^3+b^3}{2ab} $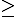 $ \dfrac{2(a+b)(a^2+b^2-ab)}{{(a+b)}^2}=\dfrac{2(a^2+b^2-ab)}{a+b} $
$ \dfrac{2(a+b)(a^2+b^2-ab)}{{(a+b)}^2}=\dfrac{2(a^2+b^2-ab)}{a+b} $ 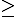 $ \dfrac{{(a+b)}^2- \dfrac{{(a+b)}^2}{2}}{a+b} =\dfrac{a+b}{2} $
$ \dfrac{{(a+b)}^2- \dfrac{{(a+b)}^2}{2}}{a+b} =\dfrac{a+b}{2} $
( $ ab $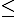 $ \dfrac{{(a+b)}^2}{4}) $
$ \dfrac{{(a+b)}^2}{4}) $
( $ 2(a^2+b^2) $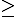 $ {(a+b)}^2)$
$ {(a+b)}^2)$
Tương tự cho 2 chú còn lại.
Cộng lại đfcm.
đfcm.
Câu 3)
a) Giải hệ
Đk: x,y
Xét PT $ x-y=(sqrt{y}-sqrt{x})(1+xy)$
Nếu x>y thì VT>0, VP <0
Nếu x<y thì VT<0 VP>0
Vậy PT có nghiệm x=y=3.
b) Chứng minh bdt
$ \dfrac{a^3+b^3}{2ab} $
( $ ab $
( $ 2(a^2+b^2) $
Tương tự cho 2 chú còn lại.
Cộng lại
Bài viết đã được chỉnh sửa nội dung bởi dehin: 05-03-2010 - 22:34
Love Lan Anh !
#7
 Đã gửi 26-03-2010 - 06:31
Đã gửi 26-03-2010 - 06:31

câu b mình xin gop ý một tí:Mình xin phần 2 câu dễ trước!
Câu 3)
b) Chứng minh bdt
$ \dfrac{a^3+b^3}{2ab} $$ \dfrac{2(a+b)(a^2+b^2-ab)}{{(a+b)}^2}=\dfrac{2(a^2+b^2-ab)}{a+b} $
$ \dfrac{{(a+b)}^2- \dfrac{{(a+b)}^2}{2}}{a+b} =\dfrac{a+b}{2} $
( $ ab $$ \dfrac{{(a+b)}^2}{4}) $
( $ 2(a^2+b^2) $$ {(a+b)}^2)$
Tương tự cho 2 chú còn lại.
Cộng lạiđfcm.
$ \dfrac{a^3+b^3}{2ab} =\dfrac{(a+b)(a^2+b^2-ab)}{2ab} \geq \dfrac{(a+b)ab}{2ab}=\dfrac{a+b}{2}$
Bài viết đã được chỉnh sửa nội dung bởi nguyen phat tai: 26-03-2010 - 06:32

0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh






