Bài viết đã được chỉnh sửa nội dung bởi mileycyrus: 02-04-2011 - 22:51

bài bđt
Bắt đầu bởi mileycyrus, 02-04-2011 - 22:50
#1
 Đã gửi 02-04-2011 - 22:50
Đã gửi 02-04-2011 - 22:50

1+ cosAcosB + cosBcosC + cosCcosA 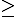 16.(cosA + cosB + cosC) + cosAcosBcosC
16.(cosA + cosB + cosC) + cosAcosBcosC
If u don't get a miracles
BECOME ONE !
BECOME ONE !
#2
 Đã gửi 03-04-2011 - 08:29
Đã gửi 03-04-2011 - 08:29

Biến đổi tương đương,ta có:$1+ cosAcosB + cosBcosC + cosCcosA \leq 16.(cosA + cosB + cosC) + cosAcosBcosC$
$2+2\sum cosAcosB \le 32\sum cosA +2cosAcosBcosC$
Sử dụng hằng đẳng thức sau:$cos^2A+cos^2B+cos^2C+2cosAcosBcosC=1$,ta thu đc kết quả sau:
$2+2\sum cosAcosB \le 32\sum cosA +1-\sum cos^2A $
$\Leftrightarrow 1+\left(\sum cosA \right)^2 \le 32\sum cosA(1)$
Đặt $t=\sum cosA \Rightarrow t \le \dfrac{3}{2}$,ta viết lại (1) dưới dạng sau:$1+t^2-32t \le 0$.Đến đây ta chỉ việc khảo sát hàm số $f(t)=1+t^2-32t$ với $t \le \dfrac{3}{2}$ là xong
Bài viết đã được chỉnh sửa nội dung bởi dark templar: 03-04-2011 - 08:30
"Do you still... believe in me ?" Sarah Kerrigan asked Jim Raynor - Starcraft II:Heart Of The Swarm.
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh




