
Đề thi chuyên toán Nguyễn Du tỉnh ĐăkLăk năm 2009-2010
#1
 Đã gửi 25-05-2012 - 09:46
Đã gửi 25-05-2012 - 09:46

ĐĂK LĂK
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2009 – 2010
MÔN TOÁN CHUYÊN
Thời gian làm bài 150 phút
Ngày thi: 26/6/2009
Bài 1: (3 điểm)
1)Giải phương trình $(x^2+2x+27)(x^2+2x+64)=2010$
2)Giải hệ$\left\{\begin{matrix} \frac{3}{\sqrt{x-y}}-\frac{2}{2x-y}=\frac{7}{3} & \\ \frac{1}{\sqrt{x-y}}+\frac{3}{2x-y}=2& \end{matrix}\right.$
Bài 2:(2 điểm)
Trong mặt phẳng toạ độ Oxy cho Parabol (P):$y=x^2$ và đường thẳng (d):$y=2kx +k^2-k+1$
1) Chứng minh đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt với mọi k
2) Gọi $x_{1},x_{2}$ là 2 hoành độ của các giao điểm.Tìm k để $x_{1}.x_{2}$ đạt GTLN
Bài 3:(2 điểm)
1) Tìm x và y nguyên sao cho $\frac{x^2}{4}=y^2+1$
2) Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh:
$a^3+b^3+c^3+2abc<a(b^2+c^2)+b(a^2+c^2)+c(a^2+b^2)$
Bài 4(2 điểm)
1) Cho tam giác ABC vuông tại A, AB =$\sqrt{2}$ cm.$\widehat{ACB}=45^0$Tính thể tích hình được tạo thành
khi quay tam giác ABC một vòng quanh BC.
2)Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Gọi M, N là tiếp tuyến chung của (O) và (O’).( M thuộc (O) và N thuộc (O'))Chứng minh AB đi qua trung điểm I của MN.
Bài 5(1điểm)
Cho tứ giác ABCD có AB = CD, BC không song song với AD. Gọi M, N lần lượt là trung điểm của BC và AD. Đường thẳng MN cắt AB tại I và cắt CD tại J.
Chứng minh:$\widehat{AIN}=\widehat{DJN}$
- L Lawliet, donghaidhtt, Dung Dang Do và 4 người khác yêu thích
#2
 Đã gửi 25-05-2012 - 10:04
Đã gửi 25-05-2012 - 10:04

Do mình không like được nữa (đạt giới hạn rồi) nên không like được, thông cảm nhéBài 1: (3 điểm)
1)Giải phương trình $(x^2+2x+27)(x^2+2x+64)=2010$
2)Giải hệ$\left\{\begin{matrix} \frac{3}{\sqrt{x-y}}-\frac{2}{2x-y}=\frac{7}{3} & \\ \frac{1}{\sqrt{x-y}}+\frac{3}{2x-y}=2& \end{matrix}\right.$

Làm bài 1 trước nhé

Bài 1:
1) Đặt $x^2+2x+27=t(t\geq 26)$ khi đó phương trình trở thành:
$t(t+37)=2010\Leftrightarrow t^2+37t-2010=0$
Xét $\Delta =37^2-4.(-2010)=9409$
$\Rightarrow t_{1}=30;t_{2}=-67$
Ta chỉ nhận giá trị $t=30$
$$t=30\Leftrightarrow x^2+2x+27=30\Leftrightarrow x^2+2x-3=0\Leftrightarrow (x+3)(x-1)=0$$
2) ĐKXĐ: $x>y$
Đặt $\frac{1}{\sqrt{x-y}}=a(a>0);\frac{1}{2x-y}=b(b>0)$, khi đó hệ trở thành:
$\left\{\begin{matrix} 3a-2b=\frac{7}{3} & \\ a+3b=2& \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1 & \\ b=\frac{1}{3}& \end{matrix}\right.$
Bài 2:Bài 2:(2 điểm)
Trong mặt phẳng toạ độ Oxy cho Parabol (P):$y=x^2$ và đường thẳng (d):$y=2kx +k^2-k+1$
1) Chứng minh đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt với mọi k
2) Gọi $x_{1},x_{2}$ là 2 hoành độ của các giao điểm.Tìm k để $x_{1}.x_{2}$ đạt GTLN
Bài 3:(2 điểm)
1) Tìm x và y nguyên sao cho $\frac{x^2}{4}=y^2+1$
1) Xét phương trình hoành độ giao điểm $x^2=2kx+k^2-k+1\Leftrightarrow x^2-2kx-k^2+k-1=0$
Xét $\Delta '=2k^2-k+1=2(k-\frac{1}{4})^2+\frac{7}{8}>0$ nên ta có đpcm
2) Vì phương trình hoành độ giao điểm luôn có nghiệm vs mọi $k$ nên theo hệ thức Viete ta có:
$$x_{1}x_{2}=-k^2+k-1=-(k-\frac{1}{2})-\frac{3}{4}\leq -\frac{3}{4}$$
Dấu "=" xảy ra khi $k=\frac{1}{2}$
Bài 3:
1) $$\frac{x^2}{4}=y^2+1\Leftrightarrow x^2=4y^2+4\Leftrightarrow (x-2y)(x+2y)=4$$
Đây là phương trình ước số quyen thuộc rồi.
Câu hình này trong cuốn sách cổ của thầy mình cho mượn mà làm không ra phải nhờ ba giải cho, kiểu này đi thi chắc chết =,=Bài 5(1điểm)
Cho tứ giác ABCD có AB = CD, BC không song song với AD. Gọi M, N lần lượt là trung điểm của BC và AD. Đường thẳng MN cắt AB tại I và cắt CD tại J.
Chứng minh:$\widehat{AIN}=\widehat{DJN}$
Bài 5:
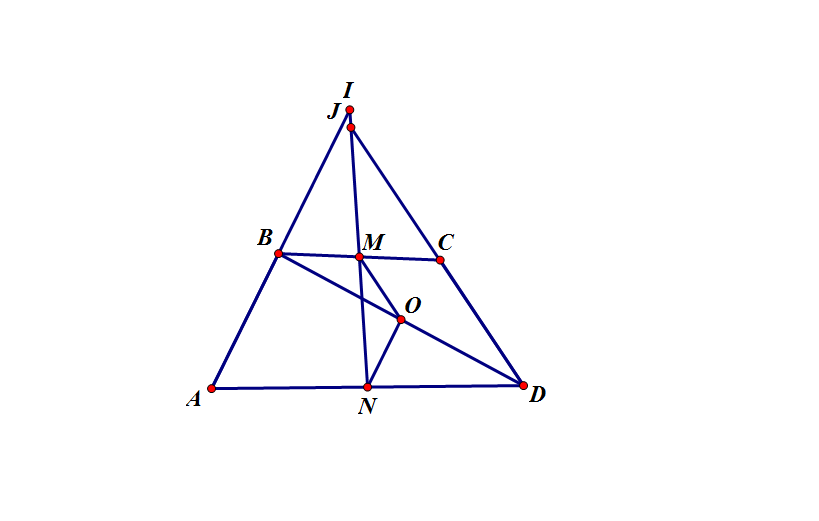
Gọi $O$ là trung điểm của đường chéo $BD$, khi đó suy ra:
- $OM$ là đường trung bình của $\Delta BCD$, suy ra $OM=\frac{1}{2}CD$ và $\widehat{OMN}=\widehat{NJD}$ (đồng vị).
- $ON$ là đường trung bình của $\Delta BAD$, suy ra $ON=\frac{1}{2}AB$ và $\widehat{ONM}=\widehat{AIN}$ (so le trong).
- donghaidhtt, NTHMyDream, hamdvk và 1 người khác yêu thích
Thích ngủ.
#3
 Đã gửi 26-05-2012 - 15:50
Đã gửi 26-05-2012 - 15:50

Bài 3Bài 3:(2 điểm)
2) Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh:
$a^3+b^3+c^3+2abc<a(b^2+c^2)+b(a^2+c^2)+c(a^2+b^2)$
Bài 4(2 điểm)
2)Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Gọi M, N là tiếp tuyến chung của (O) và (O’).( M thuộc (O) và N thuộc (O'))Chứng minh AB đi qua trung điểm I của MN.
Ta có $$a(b^2+c^2)+b(a^2+c^2)+c(a^2+b^2)=a^2(b+c)+b^2(a+c)+c^2(a+b)$$
$$\Rightarrow a^3+b^3+c^3+2abc<a^2(b+c)+b^2(a+c)+c^2(a+b)$$
$$\Leftrightarrow (a+b-c)(a+c-b)(b+c-a)>0$$
Hiển nhiên đúng
Bài 4
Gọi I là giao điểm của AB và MN
$$\Rightarrow IM^2=IA.IB=IN^2$$
$$\Rightarrow IM=IN$$
$\Rightarrow$ đpcm
Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 27-05-2012 - 17:42
- perfectstrong, L Lawliet và donghaidhtt thích
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh





