thời gian 150 phút
Môn TOÁN chuyên
Bài 1: Cho biểu thức:M = $(\frac{1+\sqrt{3}}{\sqrt{3b}(a-b)} + \frac{a+b\sqrt{3}}{b\sqrt{3a}(a-b)})\cdot (\frac{\sqrt{a^{3}b}-\sqrt{ab^{3}}}{\sqrt{a}+\sqrt{b}})$
1. Tìm điều kiện của a,b để M xác định và rút gọn M.
2. Tính giá trị của M khi a = $\sqrt{5}-2$, b = $\frac{2}{3}+\frac{\sqrt{5}}{3}$
Bài 2:Cho phương trình $x^{4}-2(m^{2}+3)x^{2}+m^{4}+5 =0$ (m là thamsố)
1. Chứng minh rằng phương trình có 4 nghiệm phân biệt $x_{1},x_{2},x_{3},x_{4}$với mọi m thuộc $\mathbb{R}$
2. Xác định m để $2x_{1}x_{2}x_{3}x_{4}$ - ($x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$) = 28
Bài 3: Tìm nghiệm nguyên của phương trình:
$x^{3}-x^{2}y+3x-2y-5=0$
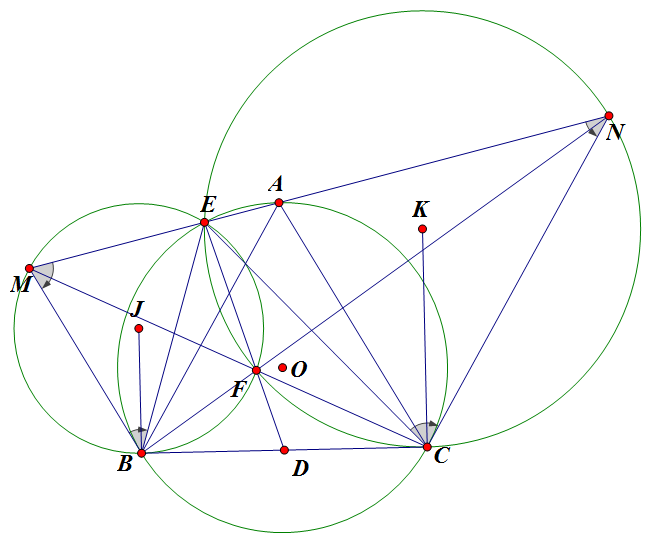
Bài 4: Cho tam giác đều ABC nội tiếp trong đường tròn (O). Một đường thẳng (d) thay đổi đi qua A, cắt (O) tại điểm thứ hai là E, cắt tiếp tuyến kẻ từ B và C của đường tròn (O) lần lượt tại M và N sao cho A,M,N nằm về 1 nửa mặt phẳng bờ BC. Gọi giao điểm thứ 2 của đường thẳng MC và BN là F. CMR:
1. $\Delta MBA$ đồng dạng với $\Delta ACN$ và tích MB$\cdot$CN không đổi.
2. BMEF là tứ giác nội tiếp.
3. Đường thẳng EF luôn đi qua 1 điểm cố định khi (d) thay đổi.
Bài 5:
Cho 4 số thực a,b,c,d thoả mãn ad-bc=$\sqrt{3}$
CMR: $a^{2}+b^{2}+c^{2}+d^{2}+ac+bd \geq 3$
Dấu đẳng thức xảy ra khi nào ?
( Thi ngày 24/6 nhưng máy mình hỏng nên hôm nay mới post đc)
Bài viết đã được chỉnh sửa nội dung bởi Lnmn179: 25-06-2012 - 17:04