Đề thi chuyên Hạ Long môn toán vòng 2.
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Câu 1: Cho biểu thức:
$A=(1-\frac{2\sqrt{a}}{a+1})\frac{1}{\sqrt{a+1}}-\frac{2}{a\sqrt{a}+\sqrt{a+a+1}})$ với$a\geq 0, a\neq 1$
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi $a=2013+2\sqrt{2012}$
Câu 2:
1.Giải hệ phương trình: $\left\{\begin{matrix} x(1+y)=5-y\\x^{2}y=4-xy^{2} \end{matrix}\right.$
2.Giải phương trình: $4x^{2}+3x+3=4x\sqrt{x+3}+2\sqrt{2x-1}$
Câu 3: Tìm $m$ để phương trình:$x^{2}-(m+2)x+m^{2}+1=0$ có hai nghiệm $x_{1},x_{2}$ thỏa mãn hệ thức: $x_{1}^{2}+2x_{2}^{2}=3x_{1}x_{2}$
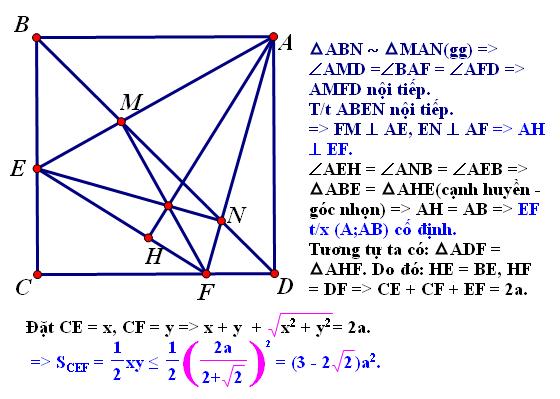
Câu 4: Cho hình vuông $ABCD$ cạnh $a$, trên cạnh$BC,CD$ lấy hai điểm $E,F$ thay đổi sao cho $\widehat{EAF}=45^{\circ}$ ($E$ thuộc $BC$, $F$ thuộc $CD$, $E$ khác $B$ và $C$). Đường thẳng $BD$ cắt hai đoạn thẳng $AE$ và $AF$ lần lượt tại $M$ và $N$. Đường thẳng đi qua $A$ và giao điểm của $EN,MF$ cắt $EF$ tại $H$.
a) Chứng minh rằng $AH$ vuông góc với $EF$
b) Chứng minh rằng $EF$ luôn tiếp xúc với 1 đường tròn cố định.
c) Tìm vị trí của $E$ và $F$ để diện tích tam giác $FEC$ đạt giá trị lớn nhất.
Câu 5: Cho 2 số thực dương $x, y$ thỏa mãn: $x+y=5$
Tìm giá trị nhỏ nhất của biểu thức: $P=\frac{4x+y}{xy}+\frac{2x-y}{4}$