Các bạn thảo luận vấn đề này nhé.
Câu hỏi: Mệnh đề sau đúng hay sai:
$$"\text{Hàm số y=f(x) có cực trị khi và chỉ khi đạo hàm f'(x) có nghiệm}"$$

[T/F] Hàm số $y=f(x)$ có cực trị khi và chỉ khi đạo hàm $f'(x)$ có nghiệm.
Bắt đầu bởi Crystal , 22-07-2012 - 13:23
#1
 Đã gửi 22-07-2012 - 13:23
Đã gửi 22-07-2012 - 13:23

#2
 Đã gửi 22-07-2012 - 15:23
Đã gửi 22-07-2012 - 15:23

Các bạn thảo luận vấn đề này nhé.
Câu hỏi: Mệnh đề sau đúng hay sai:
$$"\text{Hàm số y=f(x) có cực trị khi và chỉ khi đạo hàm f'(x) có nghiệm}"$$
Cực trị của hàm số $y=f(x)$ chính là nghiệm của phương trình $f'(x)=0$ và $f'(x)$ phải đổi dấu khi qua nghiệm đấy. Điều đó chứng tỏ nghiệm của phương trình $f'(x)=0$ phải là nghiệm đơn, còn nếu nghiệm là nghiệm kép thì giá trị $f'(x)$ là như nhau (tức hoặc cùng dương hoặc cùng âm). Vì vậy mệnh đề $"\text{Hàm số y=f(x) có cực trị khi và chỉ khi đạo hàm f'(x) có nghiệm}"$ là sai, mệnh đề đầy đủ phải là $"\text{Hàm số y=f(x) có cực trị khi và chỉ khi đạo hàm f'(x) có nghiệm và $f'(x)$ phải đổi dấu khi đi qua nghiệm đấy}"$.
Trên đây là ý kiến của e, cho nên, đáp án của e cho câu hỏi trên là SAI
Bài viết đã được chỉnh sửa nội dung bởi hoangtrong2305: 22-07-2012 - 15:24
- T M yêu thích
Toán học là ông vua của mọi ngành khoa học.
Albert Einstein
(1879-1955)

-------------------------------------------------------------------------------------------------------------------
Click xem Đạo hàm, Tích phân ứng dụng được gì?
và khám phá những ứng dụng trong cuộc sống
#3
 Đã gửi 22-07-2012 - 16:55
Đã gửi 22-07-2012 - 16:55

Bạn hoangtrong2305 còn thiếu sót 2 vấn đề sau:
1) "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm" thì vẫn đúng nhưng chỉ đúng trong trường hợp khi hàm $f'\left( x \right) = ax + b = 0,a \ne 0$ là hàm bậc nhất
2) Còn đối với các hàm có bậc hai trở lên thì nói "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm" là không đúng
Nếu nói cho chính xác hơn thì mình xin sửa lại như sau:
"Tại ${x_0}$ thì $f'\left( {{x_0}} \right) = 0$ hay không tồn tại. Thế thì hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi $f'$ đổi dấu khi $x$ đi qua ${x_0}$ ".
Tôi sẽ lấy ví dụ chứng minh câu "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm"
Ví dụ 1: Cho hàm số $y = f\left( x \right) = {x^2} + 2x + 3$. Tìm cực trị của hàm số.
Tập xác định D=R
$\begin{array}{l}
f'\left( x \right) = 2x + 2 \\
f'\left( x \right) = 0 \Leftrightarrow x = - 1 \\
\end{array}$
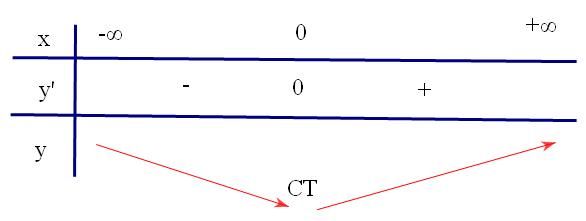
Đối với hàm bậc nhất thì câu nói trên đúng với a khác 0
Ví dụ 2: Cho hàm số $y = f\left( x \right) = \frac{1}{3}{x^3} - {x^2} + x + 1$. Tìm cực trị của hàm số trên
Tập xác định D=R
$\begin{array}{l}
y' = {x^2} - 2x + 1 = {\left( {x - 1} \right)^2} \\
y' = 0 \Leftrightarrow x = 1 \\
\end{array}$
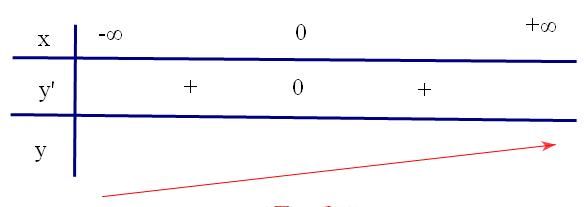
Rõ ràng $f'\left( x \right) = 0$ có nghiệm nhưng vẫn không có cực trị. Do đó câu nói trên chưa chính xác. Như vậy thì hàm số có cực trị tại ${x_0}$ khi $f'$ đổi dấu khi x qua ${x_0}$
Ví dụ 3: Cho hàm số $y = f\left( x \right) = \frac{{4 - \left| x \right|}}{{4 + \left| x \right|}}$. Tìm cực trị của hàm số trên
Tập xác định D=R vì $4 + \left| x \right| > 0,\forall x \in R$
* Nếu $x \in \left[ {0; + \infty } \right)$ thì $y = \frac{{4 - x}}{{4 + x}} \Rightarrow y' = \frac{{ - 8}}{{{{\left( {4 + x} \right)}^2}}} < 0;\forall x \in \left[ {0; + \infty } \right)$
* Nếu $x \in \left( { - \infty ;0} \right]$ thì $y = \frac{{4 + x}}{{4 - x}} \Rightarrow y' = \frac{8}{{\left( {4 - x} \right)}} > 0;\forall x \in \left( { - \infty ;0} \right]$
* Tại $x = 0$ thì $y'\left( {{0^ + }} \right) = - \frac{1}{2};y'\left( {{0^ - }} \right) = \frac{1}{2} \Rightarrow y'\left( {{0^ + }} \right) \ne y'\left( {{0^ - }} \right)$ nên $y'\left( 0 \right)$ không tồn tại
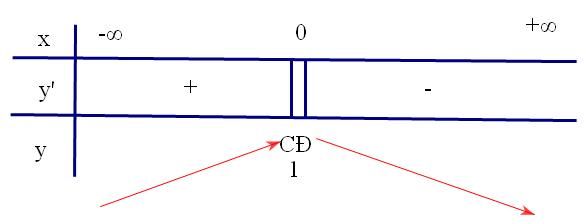
Vậy hàm số đạt cực đại tại $x = 0;{y_{CD}} = 1$. Do đó không nhất thiết ${x_0}$ là nghiệm thì mới có cực trị mà cũng có thể tại ${x_0}$ làm cho $y'\left( {{x_0}} \right) \ne 0$ vẫn có cực trị
Tóm lại: Để đúng cho tất cả mọi trường hợp thì:
"Tại ${x_0}$ thì $f'\left( {{x_0}} \right) = 0$ hay $f'\left( {{x_0}} \right) \ne 0$. Thế thì hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi $f'$ đổi dấu khi $x$ đi qua ${x_0}$ ".
1) "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm" thì vẫn đúng nhưng chỉ đúng trong trường hợp khi hàm $f'\left( x \right) = ax + b = 0,a \ne 0$ là hàm bậc nhất
2) Còn đối với các hàm có bậc hai trở lên thì nói "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm" là không đúng
Nếu nói cho chính xác hơn thì mình xin sửa lại như sau:
"Tại ${x_0}$ thì $f'\left( {{x_0}} \right) = 0$ hay không tồn tại. Thế thì hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi $f'$ đổi dấu khi $x$ đi qua ${x_0}$ ".
Tôi sẽ lấy ví dụ chứng minh câu "Hàm số $y = f\left( x \right)$ có cực trị khi và chỉ khi đạo hàm $y' = f'\left( x \right) = 0$ có nghiệm"
Ví dụ 1: Cho hàm số $y = f\left( x \right) = {x^2} + 2x + 3$. Tìm cực trị của hàm số.
Tập xác định D=R
$\begin{array}{l}
f'\left( x \right) = 2x + 2 \\
f'\left( x \right) = 0 \Leftrightarrow x = - 1 \\
\end{array}$

Đối với hàm bậc nhất thì câu nói trên đúng với a khác 0
Ví dụ 2: Cho hàm số $y = f\left( x \right) = \frac{1}{3}{x^3} - {x^2} + x + 1$. Tìm cực trị của hàm số trên
Tập xác định D=R
$\begin{array}{l}
y' = {x^2} - 2x + 1 = {\left( {x - 1} \right)^2} \\
y' = 0 \Leftrightarrow x = 1 \\
\end{array}$

Rõ ràng $f'\left( x \right) = 0$ có nghiệm nhưng vẫn không có cực trị. Do đó câu nói trên chưa chính xác. Như vậy thì hàm số có cực trị tại ${x_0}$ khi $f'$ đổi dấu khi x qua ${x_0}$
Ví dụ 3: Cho hàm số $y = f\left( x \right) = \frac{{4 - \left| x \right|}}{{4 + \left| x \right|}}$. Tìm cực trị của hàm số trên
Tập xác định D=R vì $4 + \left| x \right| > 0,\forall x \in R$
* Nếu $x \in \left[ {0; + \infty } \right)$ thì $y = \frac{{4 - x}}{{4 + x}} \Rightarrow y' = \frac{{ - 8}}{{{{\left( {4 + x} \right)}^2}}} < 0;\forall x \in \left[ {0; + \infty } \right)$
* Nếu $x \in \left( { - \infty ;0} \right]$ thì $y = \frac{{4 + x}}{{4 - x}} \Rightarrow y' = \frac{8}{{\left( {4 - x} \right)}} > 0;\forall x \in \left( { - \infty ;0} \right]$
* Tại $x = 0$ thì $y'\left( {{0^ + }} \right) = - \frac{1}{2};y'\left( {{0^ - }} \right) = \frac{1}{2} \Rightarrow y'\left( {{0^ + }} \right) \ne y'\left( {{0^ - }} \right)$ nên $y'\left( 0 \right)$ không tồn tại

Vậy hàm số đạt cực đại tại $x = 0;{y_{CD}} = 1$. Do đó không nhất thiết ${x_0}$ là nghiệm thì mới có cực trị mà cũng có thể tại ${x_0}$ làm cho $y'\left( {{x_0}} \right) \ne 0$ vẫn có cực trị
Tóm lại: Để đúng cho tất cả mọi trường hợp thì:
"Tại ${x_0}$ thì $f'\left( {{x_0}} \right) = 0$ hay $f'\left( {{x_0}} \right) \ne 0$. Thế thì hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi $f'$ đổi dấu khi $x$ đi qua ${x_0}$ ".
Bài viết đã được chỉnh sửa nội dung bởi vantho302: 22-07-2012 - 17:08
- hoangtrong2305 và T M thích
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh






