Chủ đề này có 28 trả lời

[tkvn97]

Lời nói đầu : Thưa tất cả các bạn đọc thân mến . Bất đẳng thức - Cực trị hình học là một mảng kiến thức khó trong chương trình học phổ thông , thường ít được đưa vào giảng dạy trong chương trình chính khóa . Theo xu thế ra đề hiện nay , bất đẳng thức - Cực trị hình học thường là câu chốt trong các đề thi tuyển sinh , đề thi HSG đặc biệt là trong các năm gần đây ở đề thi CASIO tỉnh Thanh Hóa luôn có phần này . Nên để đáp ứng nhu cầu của bạn đọc và nâng cao thêm trình độ của bản thân . Mình viết chuyên đề " Bất đẳng thức - Cực trị hình học " . Rất mong được sự ủng hộ của các thành viên , BQT , ĐHV để topic phát triển tốt . Xin cảm ơn .
CHUYÊN ĐỀ BẤT ĐẲNG THƯC - CỰC TRỊ HÌNH HỌC.
A.Các kiến thức cần nhớ.
I. Các bất đẳng thức thường dùng để giải toán cực trị .
1. Quan hệ giữa đường vuông góc và đường xiên .
- Trong tam giác vuông (có thể suy biến thành đoạn thẳng ) có cạnh góc vuông AH và cạnh huyền AB thì $AB \geq AH$ , xảy ra dấu bằng thì B trùng với H
- Trong tất cả các đường xiên kẻ từ một điểm nằm ngoài đường thẳng đến đường thẳng đó . Đường vuông góc có độ là dài nhỏ nhất
- Trong các đoạn thẳng nối hai điểm nằm trên hai đường thẳng song song , đoạn vuông góc với hai đường thẳng song song có độ dài nhỏ nhất .
2. Quan hệ giữa đường xiên và hình chiếu .
3. Bất đẳng thức tam giác
4. Các bất đẳng thức trong đường tròn . (SGK toán 9 )
Mở rộng : Bấ đẳng thức Pto - lê - mê . ( Đề cập trong phần bài tập)
5. Các bất đẳng thức đại số .
- Bất đẳng thúc về lũy thừa bậc chẵn. : $x^{2}\geq 0 ; -x^{2}\geq 0$
-Bất dằng thức Cauchy .
* Chú ý : Với hai số không âm x , y thì :
+) Nếu (x + y) là một hằng số thì $xy_{max}\Leftrightarrow x=y$
+) Nếu xy là hằng số thì $(x+y)_{min}\Leftrightarrow x=y$
* Bất đẳng thúc Bu - nhi - a - cop - xki . ....
II. Một số lưu ý khi giải bài toán cực trị
* Khi giải các bài toán cực trị , nhiều khi ta cần biến đổi tườn đương điều kiện cực trị của các đại lượng này thành điều kiện cực trị của đại lượng khác .
* Nhiều bài toán cực trị có liên quan đến bài toán tìm tập hợp điểm : Trong tập hợp các hình có chung một tính chất , khi cố định một số yếu tố không đổi của hình , các điểm còn lại có thể chuyển động trên một đường nhất định , việc theo dõi vị trí của chúng giúp chúng ta tìm được cực trị bài toán
* Khi giải các bài toán cực trị , có khi ta phải tìm GTLN (GTNN) trong từng trường hợp ,. rồi so sánh cá giá trị ấy với nhau để tìm GTLN )GTNN) của cả bài toán .
B. Bài tập áp dụng
(Mức độ từ dễ đến khó)
Bài tập số 1 . Cho tam giác ABC vuông tại C , D là một điểm thay đổi trên cạnh AB . Goi M , N lần lượt là hình chiếu của điểm D trên cạnh AC và BC .
Với vị trí nào của điểm D trên cạnh AB thì :
a) MN có độ dài nhỏ nhất ?
b) Diện tích tứ giác CMDN lớn nhất .
Bài tập số 2 . Trong các tam giác ABC có cùng cạnh BC và cùng diện tích , hãy tìm tam giác có chu vi nhỏ nhất.
Bài tập số 3 . Cho tứ giác ABCD nội tiếp đường tròn (O) . Chứng minh rằng :
$AC.BD\leq AB.CD+AD.BC$
(Bất đẳng thức Pto - lê - mê
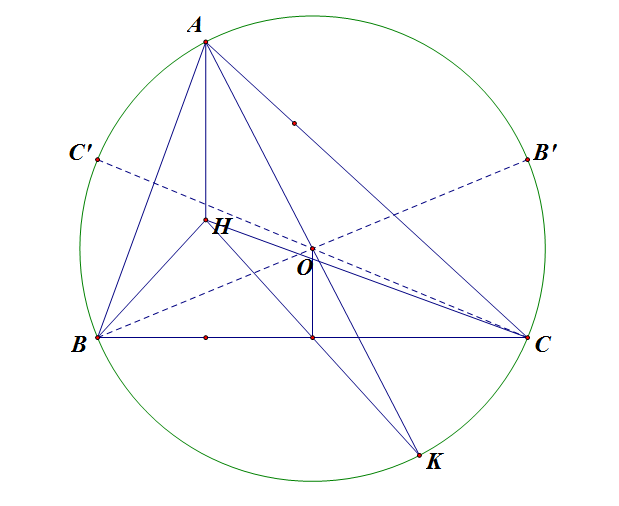
Bài tập số 4. Cho tam giác nhọn ABC nội tiếp đường tròn (O) có BC cố định $(BC\neq 2R)$, H là trực tâm . Xác định vị trí của A để : $S = HA+ HB + HC$ có giá trị lớn nhất
(Bài thi học kì II lớp 9 tỉnh thanh hóa)
Bài tập sô 5. Tính diện tích lớn nhất của tứ giác ABCD , biết AB = AD = a , BC = CD = b
Bài tập số 6. Cho đường tròn (O) dây BC là một dây cung khác đường kính của đường tròn . Tìm điểm A thuộc cung lớn BC sao cho AB + AC lớn nhất .
Bài tập sô 7.
a) Trong các hình chữ nhật có cùng chu vi ,hình nào có diện tích lớn nhất.
b) Trong các hình chữ nhật có cũng diện tích , hình nào có chu vi nhỏ nhất .
Bài tập số 8. Một hình thang có diện tích bằng 1 . Hỏi đường chéo của hình thang này độ là nhỏ nhất là bao nhiêu.
(trích đề thi GV giỏi tỉnh thanh hóa )

Bài viết đã được chỉnh sửa nội dung bởi TRUNGKIEN1997: 26-07-2012 - 09:24

[chrome98]

Giải:
1. a) Hạ $CI\perp AB$. Ta có: $MN=DC\geq IC\Rightarrow MN_{min}=IC\Leftrightarrow D\equiv I$
b)Ta có:
$\sqrt{[CMDN]}=\sqrt{MD\cdot ND}=\sqrt{\frac{MD\cdot ND+MA\cdot NB}{2}}\leq \frac{MD+ND+MA+NB}{2\sqrt{2}}=\frac{AC+BC}{2\sqrt{2}}$
$\Rightarrow \max [CMDN]=\frac{(AC+BC)^2}{8}$
$\Leftrightarrow CD$ là phân giác $\angle ACB$.

2. Theo đề bài: điểm $A$ di động trên đường song song với $BC$ là $d$, có khoảng cách cố định $=h$. Lây $D$ đối xứng với $C$ qua $d$.
Ta có: $AB+AC=AB+AD\geq BD\Rightarrow \min P_{ABC}=AB+AC+BC=BD+BC\Leftrightarrow A$ là trung điểm $BD$ hay $\triangle ABC$ cân tại $A$.

[chrome98]

Hai bài nữa:
1. Bờ rộng của một băng giấy hình chữ nhật cần phải ít nhất là bao nhiêu để có thể cắt từ băng giấy đó một tam giác đều có diện tích bằng $1$, biết chiều dài là đủ lớn.

2. Cho góc nhọn $\angle xOy$, $M$ là điểm cố đinh trong góc đó và $A,B$ di động lần lượt trên các tia $Ox, Oy$ sao cho $2012\cdot OA=2011\cdot OB$. Tìm vị trí của $A,B$ để $2012\cdot MA+2011\cdot MB$ nhỏ nhất.

[L Lawliet]

Góp ý với bạn Kiên thế này nhé: Bạn lập ra chuyên đề nào đó thì cố gắng duy trì cho tốt chứ đừng post một, hai bài rồi "quên lãng" topic đấy, các topic của bạn lập ra rất hay nhưng không duy trì được lâu dài (có topic post được 2 bài tập rồi không hoạt động nữa).
Chúc topic hoạt động tốt!

[BlackSelena]

Bài 3: Đề đúng hơn phải là cho tứ giác $ABCD$ bất kì, chứng minh $AC.BD \leq AB.CD + AD.BC$

Chứng minh
Dựng điểm $E$ trong tứ giác $ABCD$ sao cho $\triangle AEB \sim \triangle BDC$
$\Rightarrow \frac{AB}{AE} = \frac{BD}{CD}$
$\Rightarrow AB.CD = AE.BD$
Mà từ đây ta cũng có $\triangle ABD \sim \triangle BEC \text{ (c.g.c) }$
$\Rightarrow AD.BC=EC.BD$
Vậy ta có $AD.CD+AD.BC=BD(AE+EC) \geq AC.BD$
Dấu bằng xảy ra khi $ABCD:tgnt$.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 24-07-2012 - 11:54

[triethuynhmath]

Bài tập số 6. Cho đường tròn (O) dây BC là một dây cung khác đường kính của đường tròn . Tìm điểm A thuộc cung lớn BC sao cho AB + AC lớn nhất .

Bài số 6 đã có ở đây : http://diendantoanho...h-giữa-cung-ab/
Và mình đã đưa ra lời giải

[Tham Lang]

Bài toán 9.
Cho $a,b,c$ là độ dài 3 cạnh của tam giác có diện tích $S$. Chứng minh rằng :
$$3abc\ge 4\sqrt{a^2+b^2+c^2}S$$

[BlackSelena]

Bài 4:

Vẽ đường kính $AK$, $HK \cap BC = M$. Vậy ta có $HA = 2OM:const$, $HB+HC=KB+KC$
Vậy ta cần tìm $\text{ max } KB + KC$
Vẽ đường kính $BB', CC'$
Khi điểm $A$ di chuyển trên cung $B'C'$ thì $K$ cũng di chuyển trên cung $BC$, mà từ kết quả bài tập 6 cho ta $\text{ max } KB + KC \Leftrightarrow \text{ K nằm chính giữa cung BC }$.
Vậy vị trí điểm $A$ để $HA+HB+HC: \text{ max }$ là $A$ nằm chính giữa cung lớn $BC$.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 24-07-2012 - 12:23

[triethuynhmath]

Bài tập sô 7.
a) Trong các hình chữ nhật có cùng chu vi ,hình nào có diện tích lớn nhất.
b) Trong các hình chữ nhật có cũng diện tích , hình nào có chu vi nhỏ nhất .

Bài này chẳng qua là BĐT cauchy .
a)Ta có : gọi chu vi của các hình chữ nhật này là k (hằng số) . Ta có :
$a+b=\frac{k}{2}$
$S=ab\leq \frac{(a+b)^2}{4}=\frac{k^2}{16}$.
Vậy S đạt max $\Leftrightarrow a=b$.Lúc đó tứ giác ấy là hình vuông .Vậy trong các hình chữ nhật có cùng chu vi hình vuông có diện tích lớn nhất.
b) Tương tự gọi k là diện tích .Ta có :
$ab=k$
Áp dụng cauchy,ta có :
$P=2(a+b)\geq 4\sqrt{ab}=4\sqrt{k}$.
Vậy P đạt min $\Leftrightarrow a=b$.Lúc đó tứ giác ấy là hình vuông.
Kết luận...

[WhjteShadow]

Bài toán 9.
Cho $a,b,c$ là độ dài 3 cạnh của tam giác có diện tích $S$. Chứng minh rằng :
$$3abc\ge 4\sqrt{a^2+b^2+c^2}S$$

Em xin phép giải bài a Mít ạ!
Áp dụng 2 bổ đề quen thuộc:
1.$4S=\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}$
2.$(a+b+c)(a+b-c)(a+c-b)(b+c-a)=2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4$
Ta có $Q.e.D\Leftrightarrow 3abc\geq \sqrt{(a^2+b^2+c^2)(a+b+c)(a+b-c)(a+c-b)(b+c-a)}$
$\Leftrightarrow 9a^2b^2c^2\geq (a^2+b^2+c^2)[2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4]$
$\Leftrightarrow 9a^2b^2c^2(a^2+b^2+c^2)\geq (a^2+b^2+c^2)^2[2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4]$
$\Leftrightarrow 9a^2b^2c^2(a^2+b^2+c^2)\geq [2(a^2b^2+b^2c^2+c^2a^2)+a^4+b^4+c^4][2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4]$
$\Leftrightarrow 9a^2b^2c^2(a^2+b^2+c^2)+(a^4+b^4+c^4)^2\geq 4(a^2b^2+b^2c^2+c^2a^2)^2$
Đặt $a^2=x,b^2=y,c^2=z$ để biến đổi ch0 đơn giản.Ta cần chứng minh
$9xyz(x+y+z)+(x^2+y^2+z^2)^2\geq 4(xy+yz+zx)^2$
$\Leftrightarrow 9xyz(x+y+z)+x^4+y^4+z^4+2(x^2y^2+y^2z^2+x^2z^2)\geq 4[x^2y^2+y^2z^2+z^2x^2+2xyz(x+y+z)]$
$\Leftrightarrow xyz(x+y+z)+x^4+y^4+z^4\geq 2(x^2y^2+y^2z^2+z^2x^2)$
$\Leftrightarrow xyz(x+y+z)\geq 2(x^2y^2+y^2z^2+z^2x^2)-x^4-y^4-z^4$
$\Leftrightarrow xyz(x+y+z)\geq (x+y+z)(x+y-z)(x+z-y)(y+z-x)$ (Áp dụng 1 lần nữa bổ đề 2)
$\Leftrightarrow xyz\geq (x+y-z)(x+z-y)(y+z-x)$
Và đây là 1 bất đẳng thức quen thuộc.Có thể dùng AM-GM để chứng minh,cũng có thể khai triển để trở thành bất đẳng thức Schur bậc 3

Bài viết đã được chỉnh sửa nội dung bởi WhjteShadow: 24-07-2012 - 13:12

[tkvn97]

Bài số 6 đã có ở đây : http://diendantoanho...h-giữa-cung-ab/
Và mình đã đưa ra lời giải

Bày này ta có thể áp dụng hệ thức Pto - lê - mê . Cách giả này có vẻ tối ưu hơn khi ta giải một bài toán sau đây . (Bài tập số 10)

[tkvn97]

Bài tập số 10 . Cho đương tròn (O) và dây BC khác đường kính . Tìm điểm A thuộc cung lớn BC của đường tròn để tổng AB + 2AC đại giá trị nhỏ nhất .
( Đây là bài tập cần trao đổi cách làm với bạn triethuynhmath)
Bài tập số 11. Cho tam giác ABC có A > 90 nội tiếp trong đường tròn (O) . Đường phân giác trong AD của tam giác . Tìm M thuộc cung lớn BC của đường tròn (O) để MB . DC + MC .DB lớn nhất .
______________________
@BlackSelena: trao đổi thì em không có ý kiến nhưng inbox nhau cho tiện anh nhé.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 25-07-2012 - 10:59

[Tru09]

Bài 10 em thấy là lạ :
Cách *em thấy có vấn đề* mà chưa biết tại sao :??
$AB+AC \geq BC \rightarrow AB+AC+AC \geq BC$
Dấu "=" sảy ra $\leftrightarrow$ ABC là 1 đường thẳng ,và AC=0
$\rightarrow$ $AB+2AC \geq BC$ khi A trùng C
Đây có thể là 1 bài cho mọi người rút kinh nghiệm =))

[triethuynhmath]

Bài tập số 10 . Cho đương tròn (O) và dây BC khác đường kính . Tìm điểm A thuộc cung lớn BC của đường tròn để tổng AB + 2AC đại giá trị nhỏ nhất .
( Đây là bài tập cần trao đổi cách làm với bạn Trieuthuymath)

Lúc nãy mình quên $AB+2AC$ đạt GTNN thì không có chuyện Ptolemy đâu bạn à ,Tru09 làm min đúng rồi đó
Nếu là max thìcó 2 cách để xử lí những bài toán dạng này.Mình xin trình bày 1 cách sử dụng định lí Ptolemy.
Trên cung nhỏ BC ta sẽ dựng điểm D sao cho $2CD=BD$
Cách dựng:Gọi E là điểm trên đoạn BC sao cho $BE=2CE$Gọi F là điểm chính giữa cung lớn BC.FE cắt (O) tại điểm thứ 2 là D.Ta có :
DE là phân giác $\angle BDC$ $\Rightarrow \frac{BD}{CD}=\frac{BE}{CE}=2\Rightarrow BD=2CD $.Vậy ta cần điểm D cần dựng. Và tất nhiên theo cách dựng D cố định.
Áp dụng định lí Ptolemy cho tứ giác $ABCD$ nội tiếp $(O)$,Ta có:
$AB.CD+BD.AC=BC.AD\Rightarrow AB.CD+2CD.AC=BC.AD\Rightarrow (AB+2AC)=\frac{BC.AD}{CD}\leq \frac{BC.2R}{CD}$ không đổi.
Dấu "=" xảy ra khi AD là đường kính hay A là điểm đối xứng của D qua O.

Bày này ta có thể áp dụng hệ thức Pto - lê - mê . Cách giả này có vẻ tối ưu hơn khi ta giải một bài toán sau đây . (Bài tập số 10)

Bạn TRUNGKIEN1997 à đúng là hệ thức Ptolemy là tối ưu hơn khi giải quyết bài toán có hệ số khác nhau nhưng không phải lúc nào ta cũng cứng nhắc và vận dụng nó.Nói thật với bạn vì đây là diễn đàn nên thường những hệ thức như vậy ta không cần chứng minh nhưng chẳng lẽ trong những kì kiểm tra,những kì thi ,lúc mà chúng ta phải suy nghĩ ra những cách tối ưu nhất,chính xác nhất và tiết kiệm thời gian nhất thì thay vì sử dụng "cung chưa góc" để giải quyết bài toán đơn giản chúng ta lại tốn thời gian sử dụng định lí Ptolemy kia à !!!.Đương nhiên mình biết cách giải bài trên bằng định lí Ptolemy chứ khi đó D là điểm chính giữa cung nhỏ BC.Chính vì vậy theo mình thấy chúng ta cần phải biết linh hoạt trong mọi bài toán.Thậm chí bài $AB+2AC$ cũng có thể giải mà không dùng định lí Ptolemy!!! Nhưng đúng như mình nói thì trong trường hợp này Ptolemy có vẻ dễ giải quyết hơn đấy bạn à.

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 25-07-2012 - 11:22

[Tru09]

Theo :potoleme
$\rightarrow MB.CA+CM.AB =CB.AM$
Mà$ CA=\frac{AB.CD}{DB}$
$AB=\frac{CA.DB}{CD}$
$\rightarrow MB.\frac{AB.CD}{DB} +CM.\frac{CA.DB}{CD} =CB.AM$
$\rightarrow MB.DC.\frac{AB}{DB} +CM.DB.\frac{CA}{CD} =CB.AM$
Mà $\frac{AB}{DB}= \frac{CA}{CD}$
$\rightarrow (\frac{AB}{DB}).(MB.DC +CM.DB)=CB.AM$
$\rightarrow MB.DC +CM.DB =\frac{CB.AM.DB}{AB} \leq \frac{CB.(AD+DM).DB}{AB}$
Vậy Max MB.DC +CM.DB $\leftrightarrow$ AD qua M

[ntm1406]

Bài 13: Cho đường tròn (O;R) và I là điểm cố định ở bên trong đường tròn. Gọi AC và BD là hai dây bất kỳ cùng qua I. Xác định vị trí của các dây AC,BD để:
$\frac{AB.DA+BC.CD}{AB.BC+DA.CD}$
a) Lớn nhất
b) Nhỏ nhất

[henry0905]

Bài 13: Cho đường tròn (O;R) và I là điểm cố định ở bên trong đường tròn. Gọi AC và BD là hai dây bất kỳ cùng qua I. Xác định vị trí của các dây AC,BD để:
$\frac{AB.DA+BC.CD}{AB.BC+DA.CD}$
a) Lớn nhất
b) Nhỏ nhất

Ta có:
$\triangle IDC \sim \triangle IAB$
$\Rightarrow \frac{ID}{IA}=\frac{IC}{IB}=\frac{CD}{AB}$
$\triangle IAD\sim \triangle IBC$
$\Rightarrow \frac{IA}{IB}=\frac{ID}{IC}=\frac{DA}{BC}$
$\Rightarrow \frac{ID}{IB}=\frac{ID.IA}{IA.IB}=\frac{DA.CD}{AB.BC}$
$\Rightarrow \frac{ID+IB}{IB}=\frac{DA.CD+AB.BC}{AB.BC}$
$\Rightarrow BD=\frac{DA.CD+AB.BC}{AB.BC}.IB$
Ta cũng có:
$\Rightarrow \frac{IC}{IA}=\frac{IC.IB}{IB.IA}=\frac{BC.CD}{AB.AD}$
$\Rightarrow AC=\frac{AB.AD+BC.CD}{AB.AD}.IA$
$\Rightarrow \frac{AC}{BD}=\frac{AB.AD+BC.CD}{BA.BC+DA.DC}$
$\frac{AB.AD+BC.CD}{BA.BC+DA.DC}$ nhỏ nhất $\Leftrightarrow$ AC nhỏ nhất và BD lớn nhất
$\Leftrightarrow$ AC vuông góc OI và BD đi qua O
Trường hợp lớn nhất thì ngược lại:
BD vuông góc OI và AC đi qua O

[Mai Duc Khai]

5. Các bất đẳng thức đại số .
- Bất đẳng thúc về lũy thừa bậc chẵn. : $x^{2}\geq 0$ ; $-x^{2}\geq 0$

Đọc qua một hồi thì thấy cái mình bôi đỏ "công nhận là đúng "

[ducthinh26032011]

Duy trì topic nhé!
Bài 14: Cho đường tròn $(O;r)$ nội tiếp $\Delta ABC$.Kẻ đường thẳng qua $O$ cắt 2 cạnh $CA,CB$ của $\Delta$ theo thứ tự $M,N$ .Đường thẳng $MN$ ở vị trí nào thì $S_{\Delta CMN}$ đạt $min$.

Bài viết đã được chỉnh sửa nội dung bởi ducthinh26032011: 26-07-2012 - 07:47

[tkvn97]

Bài tập sô 15. Một đường thẳng di qua trọng tâm G của tam giác ABC cắt các cạnh AB , AC lần lượt tại P , Q . Chứng minh rằng :
$\frac{PQ.QC}{PA.QA}\leq \frac{1}{4}$
Bài tập số 16. Gọi a , b , c là độ dài ba cạnh của tam giác , $h_{a}; h_{b}; h_{c}$ là độ dài ba đường cao tương ứng của các cạnh đó . Tìm GTNN của tổng . $\frac{(a+b+c)^{2}}{h_{a}^{2}+h_{b}^{2}+h_{c}^{2}}$

Bài viết đã được chỉnh sửa nội dung bởi TRUNGKIEN1997: 26-07-2012 - 10:03