
Đề thi vào lớp 10 THPT Quốc học Huế
Bắt đầu bởi thuantd, 27-12-2004 - 21:03
#1
 Đã gửi 27-12-2004 - 21:03
Đã gửi 27-12-2004 - 21:03

Bài này trước đây được gửi bởi nguyendinh
Cho ngũ giác ABCDE nội tiếp trong đường tròn tâm O.AB cắt DE tại điểm M,AE cắt CD tại điểm N. K là giao điểm của BC với tiếp tuyến của đường tròn (O) qua M. Gọi P là giao điểm của hai đường tròn ngoại tiếp tam giác MAE và tam giác CEK
a)cm: M,P,K thẳng hàng
b)cm: tứ giác APNC nội tiếp
c)tính góc MPN
Đây là câu hình còn câu đại đẻ em đưa lên sau
Cho ngũ giác ABCDE nội tiếp trong đường tròn tâm O.AB cắt DE tại điểm M,AE cắt CD tại điểm N. K là giao điểm của BC với tiếp tuyến của đường tròn (O) qua M. Gọi P là giao điểm của hai đường tròn ngoại tiếp tam giác MAE và tam giác CEK
a)cm: M,P,K thẳng hàng
b)cm: tứ giác APNC nội tiếp
c)tính góc MPN
Đây là câu hình còn câu đại đẻ em đưa lên sau
#2
 Đã gửi 27-12-2004 - 21:04
Đã gửi 27-12-2004 - 21:04

Phuoctue_hue đã gửi ở diễn đàn cũ
minh nhớ câu BĐT là :
cho $a+b+c=3$
c/m: $a^4 + b^4 + c^4 \geq a^3 + b^3+ c^3$
câu giải pt ngiệm nguyên là : $\sqrt{x} + \sqrt{y} = \sqrt{147}$
còn những câu kia để mình xem lại đã
minh nhớ câu BĐT là :
cho $a+b+c=3$
c/m: $a^4 + b^4 + c^4 \geq a^3 + b^3+ c^3$
câu giải pt ngiệm nguyên là : $\sqrt{x} + \sqrt{y} = \sqrt{147}$
còn những câu kia để mình xem lại đã
Bài viết đã được chỉnh sửa nội dung bởi inhtoan: 22-05-2009 - 16:29
#3
 Đã gửi 27-12-2004 - 21:06
Đã gửi 27-12-2004 - 21:06

Và bài viết của Huynh Anh Hao
QUOTE (nguyendinh @ Jun 28 2004, 07:26 PM)
Cho ngũ giác ABCDE nội tiếp trong đường tròn tâm O.AB cắt DE tại điểm M,AE cắt CD tại điểm N. K là giao điểm của BC với tiếp tuyến của đường tròn (O) qua M. Gọi P là giao điểm của hai đường tròn ngoại tiếp tam giác MAE và tam giác CEK
a)cm: M,P,K thẳng hàng
b)cm: tứ giác APNC nội tiếp
c)tính góc MPN
Đây là câu hình còn câu đại đẻ em đưa lên sau./.
Câu a)
Ta có $\hat{KPE} = \hat{BAE}$ (cùng bù với BCE)
$\hat{MPE} =\hat{MAE} = \hat{BCE}$ do xét các tứ giác nội tiếp
Vậy $\hat{MPK} = 180^{circ}$
=> M, P, K thẳng hàng.
Câu B) mình nghĩ có vấn đề.
Câu c) $\hat{MPN} = \hat{BCE} (CMT) = ?$
Mình giải vậy có vấn đề gì không bạn
QUOTE (nguyendinh @ Jun 28 2004, 07:26 PM)
Cho ngũ giác ABCDE nội tiếp trong đường tròn tâm O.AB cắt DE tại điểm M,AE cắt CD tại điểm N. K là giao điểm của BC với tiếp tuyến của đường tròn (O) qua M. Gọi P là giao điểm của hai đường tròn ngoại tiếp tam giác MAE và tam giác CEK
a)cm: M,P,K thẳng hàng
b)cm: tứ giác APNC nội tiếp
c)tính góc MPN
Đây là câu hình còn câu đại đẻ em đưa lên sau./.
Câu a)
Ta có $\hat{KPE} = \hat{BAE}$ (cùng bù với BCE)
$\hat{MPE} =\hat{MAE} = \hat{BCE}$ do xét các tứ giác nội tiếp
Vậy $\hat{MPK} = 180^{circ}$
=> M, P, K thẳng hàng.
Câu B) mình nghĩ có vấn đề.
Câu c) $\hat{MPN} = \hat{BCE} (CMT) = ?$
Mình giải vậy có vấn đề gì không bạn
Bài viết đã được chỉnh sửa nội dung bởi inhtoan: 14-05-2009 - 12:52
#4
 Đã gửi 27-12-2004 - 21:07
Đã gửi 27-12-2004 - 21:07

tpdik2411 đã viết
cháu nghĩ là có vấn đề bác ạ: hình như góc MPN đâu có bằng góc BCE
cháu nghĩ là có vấn đề bác ạ: hình như góc MPN đâu có bằng góc BCE
#5
 Đã gửi 27-12-2004 - 21:09
Đã gửi 27-12-2004 - 21:09

Huynh Anh Hao đính chính ngay
Chết thật, lại lộn nữa rồi. Tại mình vẽ hình hơi trùng.
Có thể = 60 độ. Just guess.
Chết thật, lại lộn nữa rồi. Tại mình vẽ hình hơi trùng.
Có thể = 60 độ. Just guess.
#6
 Đã gửi 27-12-2004 - 21:10
Đã gửi 27-12-2004 - 21:10

nguyendinh nêu ý kiến
câu a đó có hai trường hợp
nếu các anh giải một trừong hợp thì bị thiếu đó
câu hình này khó là ở câu hình b và c chứ không phải là câu a đâu 9 câu a dễ quá )
còn đề đại số thì dễ rồi không cần đưa lên đâu
câu a đó có hai trường hợp
nếu các anh giải một trừong hợp thì bị thiếu đó
câu hình này khó là ở câu hình b và c chứ không phải là câu a đâu 9 câu a dễ quá )
còn đề đại số thì dễ rồi không cần đưa lên đâu
#7
 Đã gửi 27-12-2004 - 21:13
Đã gửi 27-12-2004 - 21:13

bithanhair cũng góp vui
QUOTE
minh nhớ câu BĐT là :
cho $a+b+c=3$
c/m: $a^4 + b^4 + c^4 \geq a^3 + b^3+ c^3$
$\large 3(a^4+b^4+c^4) ge (a+b+c)(a^3+b^3+c^3)$
Bài này bạn có thể sử dụng bất đẳng thức
QUOTE
minh nhớ câu BĐT là :
cho $a+b+c=3$
c/m: $a^4 + b^4 + c^4 \geq a^3 + b^3+ c^3$
$\large 3(a^4+b^4+c^4) ge (a+b+c)(a^3+b^3+c^3)$
Bài này bạn có thể sử dụng bất đẳng thức
Bài viết đã được chỉnh sửa nội dung bởi inhtoan: 22-05-2009 - 16:30
#8
 Đã gửi 27-12-2004 - 21:15
Đã gửi 27-12-2004 - 21:15

Huynh Anh Hao viết
Bài này mình có 1 cách khác như sau:
Chuyển vế ta có
VT = $a^4 - a^3 + a - 1 + b^4 + b^3 + b - 1 + c^4 - c^3 + c - 1$
= (a - 1)(a - 1)(a² + a + 1) + ...
= (a - 1)²(a² + a + 1) + ... >= 0
Vậy ta có đpcm.
Bài này mình có 1 cách khác như sau:
Chuyển vế ta có
VT = $a^4 - a^3 + a - 1 + b^4 + b^3 + b - 1 + c^4 - c^3 + c - 1$
= (a - 1)(a - 1)(a² + a + 1) + ...
= (a - 1)²(a² + a + 1) + ... >= 0
Vậy ta có đpcm.
- NTHMyDream yêu thích
#9
 Đã gửi 05-03-2005 - 15:03
Đã gửi 05-03-2005 - 15:03

tớ còn có cách giải khác cơ:
vì vai trò của a,b,c như nhau nên,ta giả sử a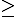 b
b 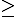 c
c
áp dụng BĐT trêbusep ta có:
$(a+b+c)(a^3+b^3+c^3) \leq (a^4+b^4+c^4).3$
theo giả thiết $a+b+c=3 \Rightarrow a^3+b^3+c^3 \leq a^4+b^4+c^4$
dấu = xảy ra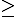 $a=b=c=1$(đpcm)
$a=b=c=1$(đpcm)
vì vai trò của a,b,c như nhau nên,ta giả sử a
áp dụng BĐT trêbusep ta có:
$(a+b+c)(a^3+b^3+c^3) \leq (a^4+b^4+c^4).3$
theo giả thiết $a+b+c=3 \Rightarrow a^3+b^3+c^3 \leq a^4+b^4+c^4$
dấu = xảy ra
Bài viết đã được chỉnh sửa nội dung bởi inhtoan: 22-05-2009 - 16:32
#10
 Khách- Snowman_*
Đã gửi 22-05-2005 - 17:28
Khách- Snowman_*
Đã gửi 22-05-2005 - 17:28
 Khách- Snowman_*
Khách- Snowman_*
Bài PT nghiệm nguyên chỉ cần để ý:
canx +cany=can147=7can3 là được.
canx +cany=can147=7can3 là được.
#11
 Đã gửi 31-05-2009 - 20:55
Đã gửi 31-05-2009 - 20:55

câu giải pt ngiệm nguyên là : $\sqrt{x} + \sqrt{y} = \sqrt{147}$
$\sqrt{x} + \sqrt{y}=7 \sqrt{3} $
Do x,y nguyên dương nên $\sqrt{x}=a\sqrt{3}$ và $y=b\sqrt{3}$ với a,b nguyên dương
$=> a\sqrt{3}+b\sqrt{3}=7 \sqrt{3}$
$=> a+b=7$
Giải với $a=1;2;3;4;5;6$
tìm $x,y$
Bài viết đã được chỉnh sửa nội dung bởi tiger_cat: 31-05-2009 - 20:56
- NTHMyDream yêu thích
Đây là chữ kí :|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh



