Ngày thứ nhất
Câu 1: Cho n là số nguyên dương. Trên mặt phẳng tọa độ $Oxy$ xét các điểm $A(0,n),B(n,n),C(n,0)$ . Hỏi có tất cả bao nhiêu cặp điểm $(M,N)$ với $M,N$ có các tọa độ nguyên , nằm trên cạnh hoặc bên trong hình vuông $OABC$ và trung điểm của $MN$ thuộc đường chéo $OB$.
Câu 2: Tìm tất cả các bộ số nguyên $(a,b,c,d)$ thỏa mãn:
$$a^2+7b^2=3c^2+2cd+5d^2$$
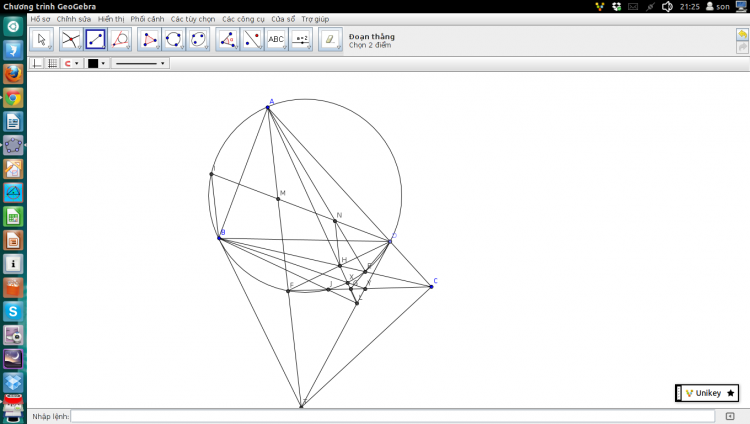
Câu 3: Cho tam giác nhọn $ABC$$,D$ là một điểm thuộc đoạn $AC$ . Giả sử đường tròn ngoại tiếp tam giác$ ABD$ cắt đoạn thẳng $BC$ tại $E$ khác $B$ . Tiếp tuyến tại $B, D$ của đường tròn ngoại tiếp tam giác$ ABD$ cắt nhau tại $T$ . $AT$ cắt đường tròn ngọai tiếp tam giác $ABD$ tại $F$ khác $A. CF$ giao$ DE$ tại $G. AG$ giao $BC$ tại $H. M$ là trung điểm của $AF$ . Chứng minh rằng $HN$ song song với $AT$.
Câu 4:
1) Một chiếc bàn có $22$ chiếc ghế. Tìm giá trị nhỏ nhất của $n$ sao cho nếu một nhóm $n$ người ngồi vào bàn thì luôn có hai người sao cho một trong hai phần của bàn bị ngăn bởi họ có đúng $2$ hoặc $8$ chiếc ghế.
2) Nếu ta xếp thêm một chiếc ghế nữa vào bàn và giữ nguyên các điều kiện còn lại thì giá trị nhỏ nhất của $n$ là bao nhiêu?