CHO $\Delta ABC$ ,O,I lần lượt là đường tròn nội và ngoại tiếp .${A}',{B}',{C}'$ lần lượt là giao điểm của đường tròn nội tiếp với BC, AC, AB ,P là trực tâm của tam giác ABC.
Chứng minh P,O,I thẳng hàng
#2
Posted 05-02-2013 - 22:55
perfectstrong
-
- Quản lý Toán Ứng dụng
-
- 5035 posts
$LOVE(x)|_{x =\alpha}^\Omega=+\infty$
$P$ phải là trực tâm của $\vartriangle A'B'C'$ chứ nhỉ?
Lời giải:
Trước hết, ta có bổ đề sau:
$\vartriangle ABC$ có trực tâm $H$, tâm đường tròn ngoại tiếp $O$. Khi đó $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$.
============================
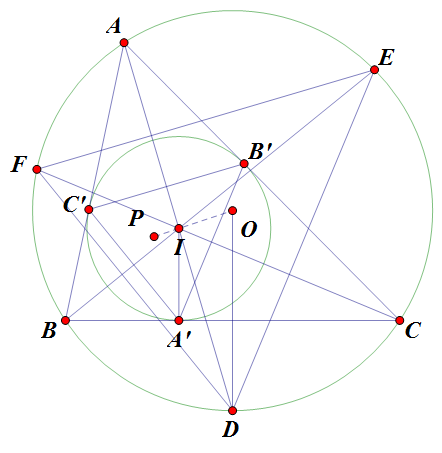
Quay lại bài toán. Vẽ $AI,BI,CI$ kéo dài, cắt $(O)$ lần thứ 2 tại $D,E,F$.
Bạn hãy tự chứng minh, $I$ là trực tâm $\vartriangle DEF$.
Theo bổ đề, ta có: $\overrightarrow{OI}=\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}\quad (1)$
Mặt khác, dễ thấy $\overrightarrow{OD}=\dfrac{R}{r}\overrightarrow{IA'}$, trong đó, $R,r$ thứ tự là bán kính của $(O),(I)$.
Tương tự, kết hợp với (1), suy ra
$\overrightarrow{OI}=\dfrac{R}{r}(\overrightarrow{IA'}+\overrightarrow{IB'}+\overrightarrow{IC'})=\dfrac{R}{r}\overrightarrow{IP}$ (áp dụng bổ đề cho $\vartriangle A'B'C'$).
Suy ra đpcm.
Lời giải:
Trước hết, ta có bổ đề sau:
$\vartriangle ABC$ có trực tâm $H$, tâm đường tròn ngoại tiếp $O$. Khi đó $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$.
============================
Quay lại bài toán. Vẽ $AI,BI,CI$ kéo dài, cắt $(O)$ lần thứ 2 tại $D,E,F$.
Bạn hãy tự chứng minh, $I$ là trực tâm $\vartriangle DEF$.
Theo bổ đề, ta có: $\overrightarrow{OI}=\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}\quad (1)$
Mặt khác, dễ thấy $\overrightarrow{OD}=\dfrac{R}{r}\overrightarrow{IA'}$, trong đó, $R,r$ thứ tự là bán kính của $(O),(I)$.
Tương tự, kết hợp với (1), suy ra
$\overrightarrow{OI}=\dfrac{R}{r}(\overrightarrow{IA'}+\overrightarrow{IB'}+\overrightarrow{IC'})=\dfrac{R}{r}\overrightarrow{IP}$ (áp dụng bổ đề cho $\vartriangle A'B'C'$).
Suy ra đpcm.
- supermember and phanquockhanh like this
Luôn yêu để sống, luôn sống để học toán, luôn học toán để yêu!!! 
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
1 user(s) are reading this topic
0 members, 1 guests, 0 anonymous users
