vslmat

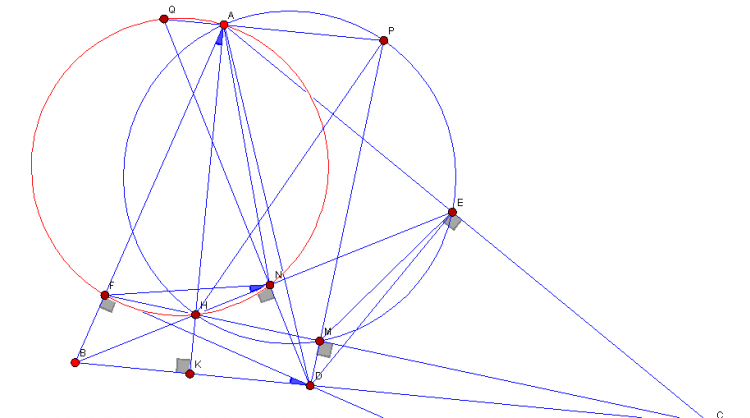
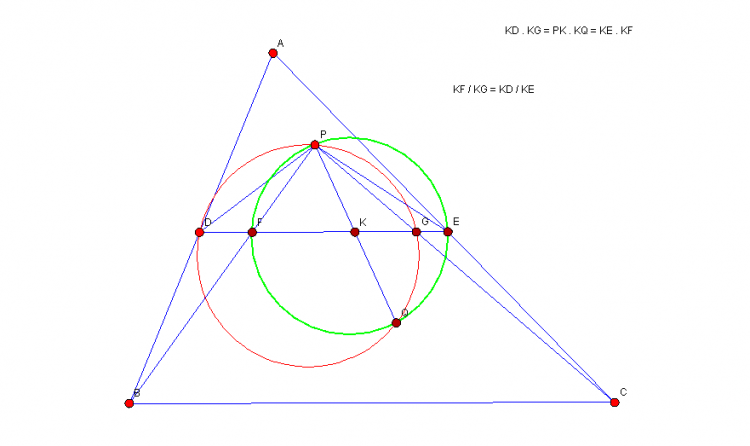
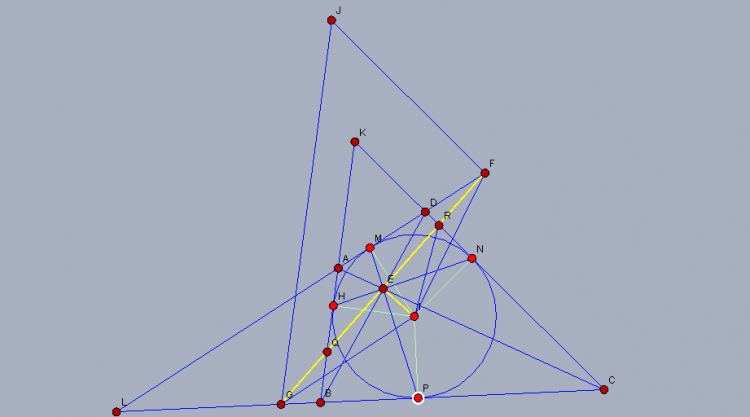
Bài 2: Cho tam giác ABC, phân giác AD, kẻ DE,DF vuông goác với AC,AB. BE cắt CF tại H; (HAE) cắt HF= M; (HAF) cắt HE tại N. DM,DN cắt (HAE);(HAF) tại P.Q. Chứng minh rằng : P,A,Q thẳng hàng.

Nhận thấy:
$\angle FAH = \angle FNB$, nhưng $\angle FAH = \angle FDB$ nên tứ giác FNDB là tứ giác nội tiếp. Vì thế $DN\perp BE$. Dẫn đến $\angle QAH = 90^{\circ}$
Tương tự như vậy vớii đường tròn thứ hai ngoại tiếp $\Delta AHE$ ta có $DM\perp CF$. Vì thế $\angle HAP = 90^{\circ}$
Ba điểm Q, A, P thẳng hàng.
Qua lời giải trên ta thấy điều kiện AD là phân giác góc A là không cần thiết.

Bài 1: Cho tam giác ABC, điểm D ở bên trong tam giác. BD, CD cắt AC,AB tại E,F. giả sử tứ giác ADEF nội tiếp. Chứng minh : Tâm đường tròn ngoại tiếp tứ giác AEDF nằm trên một đường thẳng cố định.

Bài này là một bài hình hay.

Gọi đường tròn ngoại tiếp tứ giác ANDE la $C$
Hai đường cao trong $\Delta ABC$ BG a CH cắt nhau tại trực tâm H.
Dễ thấy A, K, H, G nằm trên một đường tròn, gọi đường tròn này là $C_{1}$
Vì tứ giác AKHG cũng như tứ giác AFDE là các tứ giác nội tiếp nên H cũng như D nằm trên một đường tròn có cung BC, các điểm nằm trên cung nhỏ BC nhìn BC dưới một góc $180^{\circ} - \angle BAC$. Gọi đường tròn này là $C_{2}$, tâm của đường tròn này là S.
$C_{1}$ và $C_{2}$ cắt nhau tại một điểm khác là N. Ta sẽ chứng minh N nằm trên $C$
Nốii AN cat $C_{2}$ tạii Q. Vì $\angle HNQ = 90^{\circ}$ nên ba điểm H, S, Q thằng hàng.
Vì thế $\angle HBQ = 90^{\circ}$, cho nên BQ // AC.
$\angle ADB = \angle NQB = \angle NAE$. Tứ giác ANDE nội tiếp. N quả thật nằm trên đường tròn $C$.
Vì đường nối tâm O của $C$ với tâm L của $C_{1}$ vuông góc vớii AS nên O nằm trên đường thẳng cố định đi qua L vuông góc với AQ cố định.

Cho tam giác ABC. Một đường thẳng song song với BC cắt AB, AC tại D và E. Gọi P là một điểm bên trong tam giác ADE, F và G là giao của DE với BP và CP. Đường tròn tâm (O) ngoại tiếp tam giác PDG, đường tròn tâm (I) ngoại tiếp tam giác PEF cắt nhau tại điểm thứ hai là Q. Chứng minh rằng \[AQ \bot OI\]

Một cách giải khác:
Nhận thấy:
DK . KG = PK . KQ = FK. KE
Vì thế:

$\frac{FK}{KG} = \frac{DK}{KE}$ (*)

Điều này thực ra đã là đpcm vì giả sử KQ cắt BC tại X. Vì DE // BC và vì (*) nên A, Q, X thẳng hàng. A nằm trên PQ. Vì thế $AQ \perp OI$.

Bài Toán :


Cho trước số thực dương $v$ ; chứng minh rằng với mọi $ \triangle ABC$ ; ta có bất đẳng thức :

$ 2 \left( h^v _a r^v _ a + h^v _b r^v _ b + h^v _c r^v _ c \right) \le r^v _a r^v _ b + r^v _b r^v _ c + r^v _c r^v _ a + 3S^v \left( \dfrac{3p}{4R + r} \right)^v$

BĐT này ngoại hình đẹp quá mà lại khá chặt nên $vslmat$ loay hoay mãi vẫn không ra. Mọi người cùng xem lại, xem có ý tưởng nào hay không nhé.
Các vũ khí có thể cần dùng đến:

Với $p = \frac{a + b + c}{2}$

$r_{a} = \sqrt \frac{p(p-a)(p-c)}{p-a}$ ...

$r_{a}+r_{b}+r_{c}= 4R+r$

$\frac{1}{r} = \frac{1}{r_{a}} + \frac{1}{r_{b}}+ \frac{1}{r_{c}}$

$h_{a}= \frac{2}{a}.\sqrt{p(p-a)(p-b)(p-c)}$

$r_{a}.r_{b} + r_{b}.r_{c} + r_{c}.r_{a} = p^{2}$

và tất nhiên:

$S = r.p$

Cho tam giac ABC.Tren canh BC lay diem I sao cho $ \widehat{BAI} =x, \widehat{CAI}=y$
M,N,P lan luot la trung diem AB,AC,BC.Tren doan MN lay diem K sao cho: $ \dfrac{KM}{KN } /= \dfrac{ACsinx}{ABsiny}$
Ke duong thang(d) qua$ B va // AI$. Dung $CH\perp(d) ,(H \in (d))$
CMR: $CH.KP=S_{ABC}$

Rất tiếc là bài hình này không hay lắm mà đầu bài lại sai.
Lẽ ra điều kiện cho trước phải là:
$\frac {KM}{KN} = \frac {AC sin y}{AB sinx}$


Chứng minh:
Theo định luật sin:

$\frac{KM}{sinP_{1}} = \frac{MP}{sinK_{1}}$; $\frac{KN}{sinP_{2}} = \frac{NP}{sinK2}$

Vì $sinK_{1} = sinK_{2}$,

$\frac{KM}{KN}.\frac{sinP_{2}}{sinP_{1}} =\frac{MP}{NP} =\frac{AC}{AB}$

Có nghĩa là:

$\frac{AC.sin y}{AB.sinx}.\frac{sinP_{2}}{sinP_{1}} =\frac{AC}{AB}$

$\frac{siny}{sinx} =\frac{sinP_{1}}{sinP_{2}}$

Vì $x+y = P_{1} + P_{2}$ nên $P_{1}= y$, $P_{2}= x$

$CH = a. sin(180^{\circ} - B -x) = a. sin(B+x)$

Lại có:

$\frac{KP}{sinB} = \frac{PN}{sin(C+y)}$, vì thế, $KP = \frac{c}{2}$.$\frac{sinB}{sin(C+y)}$

Lắp vào tích:

$CH. KP =\frac {c}{2}.sinB. a.\frac {sin(B+x)}{sin(C+y)}$

Nhưng vì $sin(B+x)=sin(C+y)$ nên $CH. KP =\frac {ac.sinB}{2} = S_{\Delta ABC}$

Bài 2: Gọi $P$ là điểm bất kì trên cạnh $BC, D$ là tiếp điểm của đường tròn nội tiếp tam giác $ABC$ với cạnh $BC, Q$ và $R$ theo thứ tự là tâm nội tiếp các tam giác $ABP, ACP$. Chứng minh góc $QDR$ vuông.

Đây là một bài hình quen thuộc.

Gọi H là tiếp điểm của đường tròn $C_{1}$ nội tiếp $\Delta ABP$ với BC. F là tiếp điểm của đường tròn $C_{2}$ nội tiếp $\Delta ACP$ với BC.
Dễ thấy:
PH = $\frac{BP+AP-c}{2}$
DF = DC - FC = $\frac{a+b-c}{2} - \frac{PC+b-AP}{2} = \frac{a-c-PC+AP}{2} = \frac{BP-c+AP}{2}$
Do đó PH = DF, dẫn đến HD = PF.
Dễ thấy $\angle QPR = 90^{\circ}$. Ta muốn chứng minh $\angle QDR = 90^{\circ}$, điều này tương đương với chứng minh
($QR^2 =) QP^2+PR^2 = QD^2+DR^2$
tức là: $r_1^2+HP^2 +r_2^2+PF^2 = r_1^2+HD^2+DF^2+r_2^2$
Nhưng vì PF = HD và PH = DF, điều trên là đúng.

Bài 1: $(O)$ và $(O')$ cắt nhau tại $B$ và $M$. Các điểm $A,C$ nằm trên đường tròn $(O)$. Đường thẳng $AB$ cắt $(O')$ tại $K$ khác $B$. Đường thẳng $BC$ cắt $(O')$ tại $N$ khác $B$. Các đường trung trực của đoạn $AK$ và $CN$ cắt nhau ở $I$ khác $M$. Chừng minh góc $IMB$ vuông

Bài 2: Gọi $P$ là điểm bất kì trên cạnh $BC, D$ là tiếp điểm của đường tròn nội tiếp tam giác $ABC$ với cạnh $BC, Q$ và $R$ theo thứ tự là tâm nội tiếp các tam giác $ABP, ACP$. Chứng minh góc $QDR$ vuông.
--------------
@ WWW: Xem cách đặt tiêu đề cho bài viết tại đây.

Bạn vui lòng dành chút thời gian để xem kĩ những bài viết sau:

>> Nội quy Diễn đàn Toán học
>> Cách đặt tiêu đề phù hợp cho bài viết trên Diễn đàn để không bị ban nick
>> Hướng dẫn gửi bài trên Diễn đàn
>> Nâng cao kĩ năng gõ LATEX
>> Tra cứu công thức Toán

Bài 1: $(O)$ và $(O')$ cắt nhau tại $B$ và $M$. Các điểm $A,C$ nằm trên đường tròn $(O)$. Đường thẳng $AB$ cắt $(O')$ tại $K$ khác $B$. Đường thẳng $BC$ cắt $(O')$ tại $N$ khác $B$. Các đường trung trực của đoạn $AK$ và $CN$ cắt nhau ở $I$ khác $M$. Chừng minh góc $IMB$ vuông

Nối BO cắt $C_1$ tại D, BO' cắt $C_2$ tại G.
$\angle DMB = 90^{\circ}$, $\angle GMB = 90^{\circ}$, vì vậy 3 điểm D, M, G thẳng hàng.
DG đi qua M và vuông góc với BM.
Tứ giác CDGN là hình thang vuông.
Gọi S là trung điểm DG, $S F \perp CN$.
Tứ giác ADGK cũng là hình thang vuông, $SE \perp AK$.
Vì vậy S trùng với I. Ta có đpcm.

Từ E kẻ đường vuông góc với AB, từ F kẻ đường vuông góc với CD, hai đường này cắt nhau tại S. Đường nối tâm O của đường tròn w ngoại tiếp tứ giác ABCD với điểm S cắt đường tròn này tại L và G.
Phân giác CI cắt đường tròn này tại P, phân giác BJ cắt đường tròn này tại N.
$\angle BIC = 90^{\circ} + \frac{\Delta BAC}{2} = 90^{\circ} + \frac{\Delta BDC}{2} = \angle BJC$, tứ giác BIJC là tứ giác nội tiếp
Vì thế, $\angle AEI = \angle EIB + \angle EBI = \angle JCB + \angle EBI = \frac{1}{2} \angle DCB + \frac {1}{2} \angle ABC$
Lại có,
$\angle DFJ = \angle FJC + \angle FCJ = \angle IBC + \angle FCJ = \frac{1}{2} \angle ABC + \frac {1}{2} \angle DBC $
Như vậy, $\angle AEI = \angle DFJ$, nên $\angle SEF = \angle SFE$; SE = SF.
Như vậy đường tròn $w_1$ tâm S, bán kính SE = SF tiếp xúc với AB tại E, tiếp xúc với AC tại F. Chỉ còn phải chứng minh nó tiếp xúc với w.
$OP \perp AB$, OP // SE; $ON \perp SF$, ON//SF nên $\angle PON = \angle ESF$
Nhưng $\angle PON = 2 \angle EGF$, vì thế $\angle ESF = 2 \angle EGF$
Điều này có nghĩa là G nằm trên đường tròn $w_1$.
Vì tâm O của đường tròn w, tâm S của đường tròn $w_1$, và điểm G nằm trên một đường thẳng, $w_1$ tiếp xúc với đường tròn ngoại tiếp ABCD tại G. Ta có điều muốn chứng minh.

HAY!

Trước hết,với tứ giác ngoại tiếp, ta có các đường chéo AC, BD và các đường nối tiếp điểm MP, HN đồng qui, đây là bài toán quen thuộc.
FG cắt AB, CD tại các điểm Q a R.
Tứ giác ERNI là tứ giác nội tiếp, $\angle RNE = \angle EIR$
Tương tự, $\angle EIQ = \angle EHK$, vì vậy $\angle EIQ = \angle EIR$, QE = ER.
Các tứ giác EIPG và MEIF nội tiếp, vì vậy $\angle EIG = \angle EIP = \angle EMI = \angle EFI$, IG = IF.
Dễ dàng chứng minh MF = GP (từ G kẻ đường // với MF ...), tương tự RN = QH
MF = GP nên LF + LG = LM + LP = 2 LM (*)
Nhận thấy, $\frac{ER}{EF} = \frac{EQ}{EG}$ nên ba điểm E, K, J thẳng hàng
Vì vậy, $JF + JG = (KR+KQ). \frac{EF}{ER} = 2. KN. \frac{EF}{ER}$ (**)
Lưu ý $\frac{ER}{EF} = \frac{tan(EIR)}{tan(EIF)} = \frac{tan(RNE)}{tan(LMP)} = \frac{tan(KIN)}{tan(MIL)} = \frac{KN}{LM}$ (***)
Với (*). (**) và (***) ta có LF + LG = JF + JG (đpcm).

Chào anhqua! Tôi đã post bài hình này lên artofproblemsolving, với trích dẫn nguồn diendantoanhoc.net:

http://www.artofprob...p?f=47&t=489547
sau gần một ngày vẫn chưa có lời giải
Bài này làm tôi liên tưởng đến IMO 2012 P5 ở một số bước giải. Bạn có biết ai là tác giả bài toán này không?
P.S. Up hình: Bạn dùng phần mềm vẽ hình (tôi dùng Cinderella 2.0), sau đó export to graphic .png hay jpeg, rồi up ảnh lên.

Bài toán rất hay. Cám ơn bạn. Đây là lời giải của tôi (tôi viết trực tiếp trong Cinderella).