ChiLanA0K48

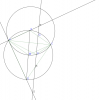
Bài toán : Trong một tứ giác lồi $ABCD$ , đường chéo $BD$ không là phân giác $\angle{ABC},\angle{ADC}.$ Điểm $P$ nằm trong tứ giác sao cho  $\angle{ABD}=\angle{CBP}$ và $\angle{ADB}=\angle{CDP}.$ Chứng minh rằng tứ giác $ABCD$ nội tiếp khi và chỉ khi $PA=PC.$

Đây là đề IMO 2004 mà

@ChiLan : hổng bit nữa, thấy bài này hay đăng lên thôi hà

Bài 1: Tam giác $ABC$ nhọn nội tiếp $(O)$. Trên đường đối trung góc $A$ của tam giác $ABC$ chọn một điểm $Q$ bất kỳ sao cho $Q$ nằm trong góc $BAC$. $(O_1), (O_2)$ lần lược là tâm đường tròn ngoại tiếp tam giác $AQB, AQC$. Chứng minh rằng trung điểm $O_1O_2$ luôn nằm trên 1 đường thẳng cố định, đường thẳng đó là đường thẳng nào.

 

Bài 2: Cho hai điểm $A,B$ phân biệt nằm trên đường tròn $(O)$ sao cho $AB$ không là đường kính. Một điểm $C$ nằm ngoài $(O)$, kẻ các tiếp tuyến $CS, CT$ đến $(O)$ với $T,S$ là các tiếp điểm. $M$ là điểm chính giữa cung nhỏ $AB$. Các đường thẳng $MS, MT$ cắt $AB$ lần lược lại $E,F$. Từ $E$ kẻ đường thẳng vuông góc với $AB$ cắt $OS$ tại $X$, từ $F$ kẻ đường thẳng vuông góc với $AB$ cắt $OT$ tại $Y$. Qua $C$ kẻ đường thẳng cắt $(O)$ tại $P,Q$ sao cho $P$ nằm giữa $C,Q$. $MP$ cắt $AB$ tại $R$.$Z$ làm tâm đường tròn ngoại tiếp $PQR$. Chứng minh $X,Y,Z$ thẳng hàng.

 

Bài 3: Tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$. $M, N$ lần lược là trung điểm cung nhỏ $AC, AB$. Điểm $G$ tùy ý trên cung nhỏ $BC$ sao cho $BG, CG >0$. Gọi $I,J,K$ lần lược là tâm đường tròn nội tiếp tam giác $ABC, AGB, AGC$. $D$ là trung điểm $MN$. $P$ là giao của $(O)$ và $(GJK)$. Chứng minh $P,I,D$ thẳng hàng.

Bài 1:

Gọi $M$ là giao điểm $OA$ với $O_1O_2$

Gọi $N$ là trung điểm $BC$

Chứng minh $\left\{\begin{matrix} \Delta OMO_1\sim \Delta CNA\\ \Delta OMO_2\sim \Delta BNA \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{OM}{CN}=\frac{MO_1}{NA}\\\frac{OM}{BN} =\frac{MO_2}{NA} \end{matrix}\right.\Rightarrow O_1M=O_2M$

suy ra $M$ thuộc đường thẳng $OA$ cố định

Bài 3:

Chứng minh được $\angle NIC=\angle KGJ\Rightarrow IKGJ$ là tứ giác nội tiếp

suy ra $G$ thuộc đường tròn ngoại tiếp tam giác $IJK$

Gọi $R$ là giao điểm $PD$ và $(O)$

Tứ giác $IKGP$ nội tiếp $\Rightarrow \angle RIC= \angle NGP\Rightarrow \angle RIN=\angle JGP$

suy ra được sđ cung $RN$ = sđ cung $MB$

suy ra $RM$ song song $NB$

Dễ dàng chứng minh $R$ là điểm chính giữa cung $BC$

chứng minh được $RN$ song song $MC$

suy ra tứ giác $RNIM$ là hình bình hành

suy ra $RN$ đi qua trung điểm $MN$

suy ra $PI$ đi qua trung điểm $D$ của $MN$

Bài 2:

Mình chưa nghĩ nhưng có thể chứng minh $CM$ vuông góc $XY$

$MX,BY$ đồng qui tại một điểm thuộc $CS$, $MY,AX$ đồng qui tại một điểm thuộc $CT$

($CT,CS$ thì tùy bạn gọi tên nha! không biết có phục vụ gì ko )

Bài IV: (4 điểm)

Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ thỏa mãn $AB<BD$ và $CA=CD.$ Gọi $E$ là trung điểm của $AD$ và $I$ là tâm đường tròn nội tiếp tam giác $ABD$. Đường tròn ngoại tiếp tam giác $BIC$ cắt $AB$ tại $F$ ($F$ khác $A,F$ khác $B$). Chứng minh rằng các đường thẳng $AI$ và $EF$ vuông góc với nhau.

Gọi $J$ là giao điểm $CE$ và $(O)$

Suy ra $J$ là điểm chính giữa cung $AD$ suy ra $IJ=IA$

Dễ dàng chứng minh $C,O,E,J$ thẳng hàng

$\angle FBI=\angle FCI\Rightarrow \angle FCI= \angle ACE\Rightarrow \left\{\begin{matrix} \Delta IFC\sim \Delta ACE\\\angle AFC=\angle ICE \end{matrix}\right.$

$\Rightarrow \Delta ACF\sim \Delta JCI $

cũng dễ dàng chứng minh $\Delta IFC\sim \Delta JAC$

Từ các tam giác đồng dạng ta có:

$\Rightarrow \left\{\begin{matrix} \frac{AE}{IF}=\frac{CA}{CI}\\ \frac{AF}{IJ}= \frac{AC}{JC}\\ \frac{IF}{JA}=\frac{CI}{CJ} \end{matrix}\right.\Rightarrow AE=AF$

suy ra tam giác $AEF$ cân tại $A$ mà $AI$ là phân giác góc $EAF$ suy ra $AI\perp EF$

P/s: Không biết có sai ở đâu ko mong mọi người chỉ giúp

Tại sao $MX$ tiếp xúc với $(I)$ vậy ạ.

Bài toán: Cho tứ giác $ABCD$ ngoại tiếp đường tròn $(O)$. $(O)$ tiếp xúc $AB,BC,CD,DA$ lần lượt tại $M,N,P,Q$. Ta có: $MP,NQ,AC,BD$ đồng quy. (chắc bạn cũng biết)

Với bài trên:

Gọi $R'$ là giao điểm của $DN$ và $(I)$

Qua $R'$ kẻ tiếp tuyến với $I$ cắt $AB,AC$ lần lượt tại $M',X'$

suy ra $CM',AX',EF,DN$ đồng qui tại $N$

Suy ra $M',X'$ trùng với $M,X$

Suy ra $R,R'$ trùng nhau.

Suy ra $MX$ tiếp xúc $(I)$ tại $R$

P/s: hình như bài này có cách dùng hàng điều hòa hay hơn bạn thử nghĩ xem nhé

Bài toán : Phép đối xứng qua các cạnh $BC,AC,AB$ của tam giác $ABC$ có $3$ góc nhọn biến đường thẳng $Euler$ của tam giác $ABC$ tương ứng thành các đường thẳng $d_1,d_2,d_3.$ Chứng minh rằng các đường thẳng đó cắt nhau tại một điểm nằm trên đường tròn ngoại tiếp tam giác $ABC.$

Gọi $A',B'$ lần lượt là giao điểm của $AH,BH$ với đường tròn ngoại tiếp tam giác $ABC$

Dễ dàng chứng minh $A',B'$ là các ảnh của $H$ qua phép đối xứng qua $BC,CA$

suy ra $A',B'$ lần lượt thuộc $d_1,d_2$

Gọi $M$ là giao điểm $d_1,d_2$

Gọi $K,L$ là giao điểm đường thẳng $Euler$ của tam giác $ABC$ với $BC,CA$

Qua phép đối xứng suy ra $\angle LHB'=\angle LB'H= \angle KHB= \angle KA'B$

Suy ra Tứ giác $BA'MB'$ nội tiếp

suy ra $M$ thuộc đường tròn ngoại tiếp tam giác $ABC$

Chứng minh tương tự suy ra $d_1,d_2,d_3$ đôi một cắt nhau

suy ra ba đường thẳng đồng quy tại một điểm thuộc đường tròn ngoại tiếp tam giác $ABC$

P/s: hình như nó đúng với mọi đường thẳng qua trực tâm $H$

Đề: Cho tam giác $ABC$ không cân tại $A$, ngoại tiếp $(I)$. Gọi $D,E,F$ lần lược là tiếp điểm của $(I)$ lên $BC,CA,AB$.

$ED$ giao $AB$ tại $P$

$M$ thuộc đoạn $AB$

$N$ là giao điểm của $CM$ và $ EF$

$Q$ là giao điểm của $PN$ và $AC$

Chứng minh $IM \bot FQ$

Gọi giao điểm của $BN$ và $AC$ là $X$

Gọi giao điểm của $ME$ và $BQ$ là $S$

Gọi giao điểm của $FQ$ và $XM$ là $R$

Áp dụng địng lí Pappus

suy ra $R,S,N$ thẳng hàng và $S,N,D$ thẳng hàng

suy ra $R,N,D$ thẳng hàng

Mặt khác chứng minh được $MX$ tiếp xúc đường tròn $(I)$ và $EF,BX,CM$ và đường thẳng nối $D$ với tiếp điểm tại $MX$ đồng qui suy ra $R$ là tiếp điểm của $(I)$ với $MX$

Suy ra $FR$ là đường đối cực của $M$ với $(I)$

Suy ra $Q$ thuộc đường đối cực của $M$ với $(I)$ suy ra $MI\perp FQ$

Cho hình chữ nhật ABCD. E là trung điểm AB. Đường thẳng qua E vuông góc với BD cắt BC tại F. Biết D(1;8), phương trình AF 5x+7y-36=0 và E thuộc đường thẳng x+y+3=0. Tìm tọa độ B,C

Gọi $P$ là giao điểm $BD$ và $EF$

$BD\perp EF\Rightarrow \angle DPF=90^{o}$

$\Rightarrow P,F$ cùng thuộc đường tròn đường kính $DF$

$\Rightarrow BP.BD=BC.BF$

$E,P$ thuộc đường tròn đường kính $ED$

$\Rightarrow BE.BA=BP.BD$

$\Rightarrow BE.BA=BC.BE$

$\Rightarrow$ tứ giác $AECF$ là tứ giác nội tiếp

$\Rightarrow \angle BEC=\angle BFD\Rightarrow \angle FAD=\angle DEA\Rightarrow AF\perp DE$

Từ đây dễ viết được phương trình đường thẳng $DE$

Tìm được toa độ $E$

mà $E$ là trung điểm $AB$

Đặt ẩn tọa độ $A$

dễ tìm đc tọa độ các đỉnh

có một người ngày nào cũng chơi cờ, nhưng 1 tuần anh ta không chơi quá 13 ván cờ.chứng minh rằng tồn tại 1 số ngày liên tiếp mà anh ta chơi đúng 20 ván.

Xét trong 21 ngày liên tiếp kể từ một ngày nào đó

Gọi $S(n)$ là tổng số ván cờ anh ta đánh tính đến ngày thứ $n$ với $1\leq n\leq 21$

Suy ra ta luôn có $S(m)\neq S(n)$ $\forall m\neq n$ $1\leq m,n\leq 21$

$\Rightarrow 0\leq S(n)\leq 3\times 13=39$

Vì có 21 tổng nên tồn tại ít nhất 2 tổng $S(m), S(n)$ với $n<m$ sao cho:

$S(m)\equiv S(n)(mod20)\Rightarrow S(m)-S(n)\equiv 0(mod20)$ mà $0<S(m)-S(n)<39$

suy ra $S(m)-S(n)=20$ suy ra từ ngày thứ $n+1$ đến ngày thứ $m$ anh ta đã chơi đúng 20 ván

   Giải hệ phương trình :

 

    $\left\{\begin{matrix} x^2(y+z)^2=(3x^2+x+1)y^2z^2 & & \\ y^2(x+z)^2=(4y^2+y+1)x^2z^2 & & \\ z^2(x+y)^2=(5z^2+z+1)x^2y^2& & \end{matrix}\right.$

$x=0$;$y=0$;$z=0$ là một nghiệm của hệ phương trình

Với $x\neq 0; y\neq 0; z\neq 0$

$\Rightarrow \left\{\begin{matrix} \frac{x^{2}}{3x^2+x+1}=\frac{y^{2}z^{2}}{(y+z)^{2}}\\ \frac{y^{2}}{4y^{2}+y+1}=\frac{z^{2}x^{2}}{(z+x)^{2}}\\ \frac{z^{2}}{5z^{2}+z+1}=\frac{x^{2}y^{2}}{(x+y)^{2}} \end{matrix}\right.$

$\Rightarrow \left\{\begin{matrix} \\3+\frac{1}{x}+\frac{1}{x^{2}}=\left ( \frac{1}{y}+\frac{1}{z} \right )^{2} \\4+\frac{1}{y}+\frac{1}{y^{2}}=\left ( \frac{1}{z}+\frac{1}{x} \right )^{2} \\ 5+\frac{1}{z}+\frac{1}{z^{2}}=\left ( \frac{1}{x}+\frac{1}{y} \right )^{2} \end{matrix}\right.$

$\Rightarrow \left ( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )^{2}-\left ( \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \right )-12=0$

Từ đó tìm $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$ thay vào hệ giải ra $x,y,z$

Giải phương trình Logarit:

$log_{2}(4^{x}+4)=x-log_{\frac{1}{2}}(2^{x+1}-3)$

$\Leftrightarrow log_{2}\left ( 4^{x}+4 \right )=x+log_{2}\left ( 2^{x+1}-3 \right )$

$\Leftrightarrow log_{2}\frac{4^{x}+4}{2^{x+1}-3}=x$

$\Leftrightarrow \frac{4^{x}+4}{2^{x+1}-3}=2^{x}$

$\Leftrightarrow 4^{x}+4=2^{2x+1}-3.2^{x}$

$\Leftrightarrow 4^{x}-3.2^{x}-4=0$

Bài toán :

Cho tam giác $ABC$, $M$ là điểm nằm trong tam giác sao cho $M$ không thuộc đường cao của tam giác. Các đường thẳng qua $M$ vuông góc với $MA,MB,MC$ lần lượt cắt $BC,CA,AB$ tại $A',B',C$. Chứng minh rằng: $A',B',C'$ thẳng hàng.

P/s: mình thấy kết quả này lúc tìm cách chứng minh bài 1. Chắc kết quả quen thuộc nhưng bạn nào mới học có thể làm thử.

Với n là số nguyên dương, cmr:

$\sum_{k=0}^{n-1}C_{2n+1}^{2(n-k)}.C_{n-k}^{1} \vdots 4^{n-1}$

$S=\sum _{k=0}^{n-1}C_{2n+1}^{2(n-k)}.C_{n-k}^{1}=\sum _{k=0}^{n-1}(n-k)C_{2n+1}^{2(n-k)}=\sum _{i=1}^{n}iC_{2n+1}^{2i}=\frac{1}{2}\sum _{i=1}^{n}2iC_{2n+1}^{2i}=\frac{2n+1}{2}\sum_{i=1}^{n}C_{2n}^{2i-1}=\frac{2n+1}{2}.\frac{(1+1)^{2n}-(1-1)^{2n}}{2}=\left ( 2n+1 \right ).2^{2n-2}$

suy ra đpcm

1, Cho k,n là các số nguyên dương và $k\leqslant n$ CMR:

$C_{n}^{0}C_{n}^{k}+C_{n}^{1}C_{n}^{k+1}...+C{n}^{n-k}C{n}^{n}=C_{2n}^{n+k}$

 

2.Cho m,n là số nguyên dương.CMR:

$C_{m}^{0}+C_{m+1}^1+...+C_{m+n}^{n}=C_{m+n+1}^{n}$

Bài 1:

Xét khai triển $\left ( x+1 \right )^{n}.\left ( \frac{1}{x}+1 \right )^{n}=\sum_{i=0}^{n}C_{n}^{i}.x^{i}\sum _{j=0}^{n}C_{n}^{j}.x^{-j}=\sum _{i=0}^{n}\sum _{j=0}^{n}C_{n}^{i}.C_{n}^{j}.x^{i-j}$

Hệ số của $x^{k}$ trong khai triển trên là $\sum _{i=0}^{n}\sum _{j=0}^{n}C_{n}^{i}.C_{n}^{j}$ với $i-j=k\Leftrightarrow i=j+k$

$\Rightarrow$ hệ số sẽ bằng $\sum_{j=0}^{n}C_{n}^{j}.C_{n}^{k+j}$

Mặt khác $\left ( x+1 \right )^{n}.\left ( \frac{1}{x}+1 \right )^{n}=\frac{\left ( x+1 \right )^{2n}}{x^{n}}=\sum _{i=0}^{2n}C_{2n}^{i}.x^{i-n}$

Hệ số của $x^{k}$ trong khai triển là $\sum_{i=0}^{2n}C_{2n}^{i}$ với $i-n=k\Leftrightarrow i=n+k$ $\Rightarrow$ hệ số là $C_{2n}^{n+k}$

$\Rightarrow \sum_{j=0}^{n}C_{n}^{j}.C_{n}^{k+j}=C_{2n}^{n+k}$

đpcm

Bài 2:

Đẳng thức cần chứng minh tương đương với $\sum_{i=0}^{n}C_{i+n}^{m}=C_{n+m+1}^{m+1}$

Xét $\sum_{i=0}^{n}\left ( 1+x \right )^{m+i}=\frac{\left ( 1+x \right )^{n+m+1}-(1+x)^{m}}{x}$

$\sum_{i=0}^{n}(1+x)^{i+m}=\sum _{i=0}^{n}\sum_{j=0}^{i+m}C_{i+m}^{j}.x^{j}$

$\Rightarrow$ hệ số của $x^{m}$ trong khai triển trên là $\sum_{i=0}^{n}C_{i+m}^{m}$

Mặt khác hệ số của $x^{m}$ là hệ số của $x^{m}$ trong $\frac{\left ( 1+x \right )^{m+n+1}-\left ( 1+x \right )^m}{x}$ và bằng $C_{m+n+1}^{m+1}$

suy ra đpcm

BÀI TOÁN 1

Cho tam giác ABC ,H là trực tâm tam giác. M là một điểm bất kì trong tam giác,kẻ đường thẳng qua M vuông góc với HA,HB,HC cắt BC,CA,AB,lần lượt tại X,Y,Z.Chứng minh rằng:X,Y,Z thẳng hàng

Có cần xem lại đề bài không bạn? $H$ là trực tâm tam giác $ABC$ $\Rightarrow HA \perp BC$ kẻ đường thẳng qua $M$ vuông góc $HA$ cắt $BC$ tại $X$ sao được

Bài 4. (3đ)

Giải hệ phương trình $\left\{\begin{matrix} 2x^3+2y^2+y+1=0\\ 2y^3+2z^2+z+1=0 \\ 2z^3+2x^2+x+1=0 \end{matrix}\right.$

hệ phương trình tương đương

$\left\{\begin{matrix} y^{2}+\frac{y}}{2}+\frac{1}{2}=-x^{3}\\ z^{2}+\frac{z}{2}+\frac{1}{2}=-y^{3}\\ x^{2}+\frac{x}{2}+\frac{1}{2}=-z^{3} \end{matrix}\right.$

$\Leftrightarrow -x^{3}=y^{2}+\frac{y}{2}+\frac{1}{2}\geq \frac{7}{16}> \frac{1}{8}\Rightarrow x< \frac{-1}{2}$

Chứng minh tương tự $\Rightarrow y< \frac{-1}{2}; z< \frac{-1}{2}$

Không mất tổng quát giả sử $x$ là số lớn nhất trong 3 số $x,y,z$

$\Rightarrow x^{3}-z^{3}=x^{2}+\frac{x}{2}-y^{2}-\frac{y}{2}=(x-y)\left ( x+y+\frac{1}{2} \right )\leq 0$

$\Rightarrow x\leq z\Rightarrow x=z$

tương tự suy ra $x=y=z$

$\Rightarrow 2x^{3}+2x^{2}+x+1=0\Rrightarrow x=y=z=-1$