viet nam in my heart

Bài hình là bài khá quen thuộc. Bài này là bài thi ngày $1$ của Hàn Quốc năm $2015$

Cấu hình này cũng đã có ở đây trên diễn đàn ( Chắc cùng từ bài của Hàn Quốc mà ra  ) http://diendantoanho...-tụy-ninh-bình/ Xin trích lại lời giải luôn

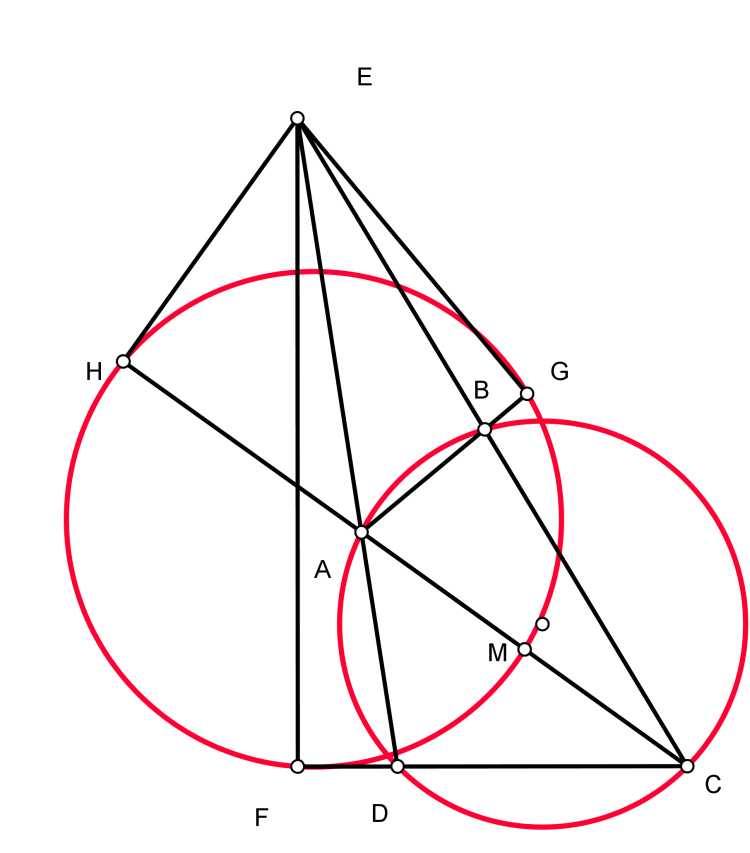
Câu 2 (3 điểm).Cho tam giác ABC nhọn,không cân nội tiếp đường tròn (O;R),ngoại tiếp đường tròn (I,r).G là trung điểm đoạn BC.Đường tròn (I;r) tiếp xúc với BC,CA,AB lần lượt tại D,E,F.Đường thẳng EF cắt đường tròn (O) tại M,N.Trên tia đối của tia OG lấy điểm H sao cho OH=R+r

 

a)Chứng minh M,N,D,G cùng nằm trên đường tròn tâm K

 

b)Chứng minh rằng K,D,H thẳng hàng

Untitled13.png

a) Kéo dài $MN$ cắt $BC$ tại $J$. Dễ chứng minh $(JDBC)=-1$, từ đó kết hợp với hệ thức Maclaurin suy ra $JD.JG=JM.JN$ 

=> ĐPCM

b) $OH$ cắt $(O)$ tại $P$ suy ra $PH=ID$, mà $PH//ID$ nên $PHID$ là hình bình hành.

Suy ra trung điểm $L$ của $DH$ cũng là trung điểm $L$ của $PI$.

Mặt khác dễ chứng minh góc $IAP$ vuông (dựa vào tính chất $AI$ cắt $(O)$ tại điểm chính giữa cung $BC$) nên dễ suy ra $APNM$ là hình thang cân.

$L$ thuộc trung trực của $AP$ nên $L$ cũng thuộc đường trung trực của $MN$.

Mà $L$ cũng là đường trung trực của $DG$ (dễ chứng minh).

Do đó $L\equiv K$ hay $K,D,H$ thằng hàng (đpcm)

Còn đây là links bài toán http://www.artofprob...1065214p4625207

Bài 3 ngày 1 là một bài quen thuộc về bất biến và từng xuất hiện trong topic đề thi mẫu hướng tới VMO 2016 tại đây.

 

Bài 6 ngày 2 có thể giải không cần sử dụng định lí Thebault mà chỉ cần sử dụng phương tích với định lí Thales là được, cụ thể :

Gọi $X,Y$ lần lượt là tiếp điểm của $\odot (O_1),\odot (O_2)$ với $BC$. $Z,T$ lần lượt là tiếp điểm của $\odot (O_1),\odot (O_2)$ với $\odot (O)$.

Theo định lí Thales $ZX,TY$ đi qua điểm chính giữa cung $AB$ không chứa $C$. Gọi điểm đó là $D$.

Theo định lí về tâm đẳng phương thì $CT,ZX,TY$ đồng quy nên $C,T,D$ thẳng hàng.

Ta có $DT^2=\overline{DX}\cdot \overline{DZ}=DA^2$ nên $T$ là tâm đường tròn nội tiếp $\triangle ABC$.

 

PS. Mình nghĩ có thể đây là bài đề nghị của THPT chuyên Hùng Vương Phú Thọ cho cuộc thi Duyên Hải 2016 nên không thể nói là sao chép được!

Bài này là đề nghị của Chuyên Lê Quý Đôn Đà Nẵng em ạ. Bài $3$ ngày một dùng bất biến thì có lẽ tác giả cũng đã đổi đi cho phù hợp với địa phương thì có thể ổn. Nhưng đến bài $7$ tổ hợp ngày $2$ nếu ai có đọc qua về phương pháp song ánh thì cũng sẽ biết ngay đây là một bài trong $Romani TST 2002$. 

PS. Theo quan điểm của mình có lẽ vấn đề này cũng nên chấm dứt tại đây 

Ngày 1:

Bài 1: Xét dãy số thực vô hạn $x_1,x_2,...,x_n$ thỏa mãn 

$|x_{m+n}-x_{m}-x_{n}| < \dfrac{1}{m+n}$ với mọi số nguyên dương $m,n$

Chứng minh rằng $(x_n)$ là cấp số cộng

Bài 2: Cho tam giác $ABC$ ngoại tiếp $(I)$. Các cạnh $AB,AC$ tiếp xúc với $(I)$ tại $E,F$. Đường thằng qua $B$ song song với $AC$ cắt $EF$ tại $K$. $CK$ cắt $AB$ tại $G$. Chứng minh tam giác $AIG$ vuông

Bài 3: Một hàng cây bưởi Đoan Hùng gồm $17$ cây thẳng hàng đánh số cây theo thứ tự là các số tự nhiên từ $1$ đến $17$. Ban đầu mỗi cây có một con đậu trên đó để hút mật hoa. Sau đó, cứ mỗi giờ có hai con ong nào đó bay sang hai cây bên cạnh để tìm và hút mật nhưng theo hai chiều ngược nhau. Hỏi sau giờ có hay không trường hợp mà 

a) Không có con ong ở cây có số thứ tự chẵn 

b) Có $9$ con ong ở cây cuối cùng 

Bài 4: Tìm tất cả các đa thức hệ số nguyên $P(x)$ khác đa thức không sao cho $10^n-3n-2016$ chia hết cho $P(n)$ với mọi số nguyên dương $n$

Ngày 2:

Bài 5: Tìm tất cả các đa thức $P(x)$ hệ số thực thỏa mãn

$$(x^2-6x+8)P(x)-(x^2+2x)P(x-2)=6x^2-12x$$ 

Bài 6: Cho đường tròn $(O)$ và dây cung $AB$. Các đường tròn $(O_1)$ và $(O_2)$ nằm về một phía đối với đường thẳng $AB$, Tiếp xúc với nhau tại $T$ đồng thời tiếp xúc trong với đường tròn $(O)$. Tiếp tuyến chung tại $T$ của $(O_1),(O_2)$ cắt đường tròn $(O)$ tại $C$ (Với $C$ thuộc nửa mặt phẳng bờ $AB$ chứa $(O_1),(O_2)$). Chứng minh rằng $T$ là tâm đường tròn nội tiếp tam giác $ABC$

Bài 7: Với mỗi số nguyên dương $n$, gọi $f(n)$ là số cách chọn các dấu cộng, trừ trong biểu thức $E_n= \pm 1 \pm 2 \pm \dots \pm n$ sao cho $E_n=0$. Chứng minh rằng

a) $f(n)=0$ khi $n \equiv 1,2 (mod 4)$ 

a) Khi $n \equiv 0,3 (mod 4)$ ta có $\dfrac{\sqrt{2^n}}{2} \leq f(n) \leq 2^n -2^{1+[\dfrac{n}{2}]}$

Đề này lấy khá nhiều bài từ các đề khác cụ thể là bài tổ hợp và bài hình ngày $2$   

$s_{n}$ là giá trị của hàm mà có phải là giá trị của biến đâu?

em đọc nhầm đề ạ 

Nếu gọi $t_{n}$ là dãy nghiệm thì $t_{n}$ bị chặn giữa $0,1$ nên từ đó $s_{n}$ cũng bị chặn giữa $0,1$

Do tính nhỏ nhất nên $s_{n+1}=f_{n+1}(t_{n+1})<f_{n+1}(t_{n})=t_{n}^{2n+2}+t_{n}^{2n+1}+s_n<s_{n}$

Do đó $s_{n}$ là dãy giảm

Do đó nó có giới hạn hữu hạn

Bài 1 ngày 2:

Trước hết dễ chứng minh với $n$ là lũy thừa của $3$. Vì khi đó ta chọn $m=111...11$($n$ số 1)

Cần chứng minh $\dfrac{10^n-1}{9} \vdots n$ (áp dụng bổ đề $LTE$ cho ta điều phải chứng minh)

Với $n$ không là lũy thừa của $3$ ta thấy tồn tại số $x$ sao cho $3^{x}<n<3^{x+1}$

Khi đó ta sẽ chọn $S(m)=3^{x+1}$

Tức là chỉ ra tồn tại số $m$ có tổng các chữ số là $3^{x+1}$ và $m \vdots 3^{x+1}$

Nếu $n\leq2.3^x$

Đặt $n=3^x+t$

Ta sẽ chọn luôn $m=111...1333...3222...2$ trong đó gồm $t$ số $1$, $t$ số $2$ và $3^x-t$ số $3$

Ta chứng minh số này chia hết cho $3^{x+1}$

Sau khi biến đổi ta thu được $m=\dfrac{(10^t+2)(10^{3^{x}}-1)}{9} \vdots 3^{x+1} $ ( Dễ chứng minh theo bổ đề $LTE$)

Nếu $n>2.3^x$. 

Đặt $n=2.3^x+t$

Ta sẽ chọn $m=111...1222...21.....1$ thứ tự từ trái sang phải là gồm $3^x+t$ số $1$, $3^x-t$ số $2$ rồi lại $t$ số $1$

Ta chứng minh số này chia hết cho $3^{x+1}$

Sau khi biến đổi ta thu được $m=\dfrac{(10^{3^{x}+t}+10^t+1)(10^{3^{x}}-1)}{9} \vdots 3^{x+1} $ ( Dễ chứng minh theo bổ đề $LTE$)

 

ĐỀ THI CHỌN ĐỘI TUYỂN QUỐC GIA THPT CHUYÊN KHTN - ĐHQG HÀ NỘI VÒNG 1 NGÀY 2 NĂM 2016

 

Bài 3. Tứ giác $ABCD$ nội tiếp $(O)$ sao cho $ABCD$ không phải là hình thang. Tiếp tuyến tại $C,D$ của $(O)$ cắt nhau tại $T.TA$ giao $BD$ tại $S.E$ đối xứng $B$ qua $S.AB$ cắt đường tròn ngoại tiếp tam giác $EBC$ tại $F.EC$ giao $TA$ tại $P$.

a, Chứng minh rằng $PF$ tiếp xúc đường tròn ngoại tiếp tam giác $EBC$.

b, Giả sử $PF$ cắt $AC$ tại $Q. H, K$ lần lượt là hình chiếu của $Q$ lên $F A, F C. M$ là trung điểm $FA$. Chứng minh rằng tiếp tuyến qua $A$ của $(O)$ và đường thẳng qua $Q$ song song với $AO$ cắt nhau trên đường tròn ngoại tiếp tam giác $MHK$.

 

Mình xin nếu ý tưởng giải bài hình. Phần $a$ khá đơn giản còn phần $b$ có lẽ tác giả đã chế ra từ một bài toán quen thuộc

a) Dễ dàng chứng minh được : $\triangle ECF \backsim \triangle DCA$

Ta cần chứng minh $\dfrac{PC}{PE}= \dfrac{FC^2}{FE^2}=\dfrac{AC^2}{AD^2}$ 

Mặt khác $\dfrac{PC}{PE}=\dfrac{d(C,AT)}{d(E,AT)}=\dfrac{d(C,AT)}{d(D,AT)}$ (Do $D,E$ đối xứng qua $T$)

Do đó chỉ cần chứng minh$ \dfrac{d(C,AT)}{d(D,AT)}=\dfrac{AC^2}{AD^2}$  (bổ đề quen thuộc với  $AT$ là đường đối trung của $\triangle ACD$)

b)

Dễ thấy nếu gọi $X$ là giao điểm của tiếp tuyến tại $A$ của $(O)$ và $PF$ (Tiếp tuyến tại $F$ của $(BCE)$) thì ta được tứ giác $CFXA$ nội tiếp

Từ đó quy bài toán về cấu hình quen thuộc sau: Tứ giác $ABCD$ nội tiếp có $AD$ cắt $BC$ tại $E$. Gọi $F,G,H$ lần lượt là hình chiếu của $E$ trên $AB,CD,AC$ và $M$ là trung điểm $AC$ thì sẽ có $F,G,H,E$ đồng viên

Có thể nhìn điểm $E$ ở ngoài hơi khó nhưng thực chất cách chứng minh nó giống với trường hợp ở trong như sau

Tứ giác $ABCD$ nội tiếp có $AC$ cắt $BD$ tại $E$. Gọi $F,G,H$ lần lượt là hình chiếu của $E$ trên $AD,BC,AB$ và $M$ là trung điểm $AB$ thì sẽ có $F,G,H,E$ đồng viên

Cấu hình khá quen thuộc và nó đã từng xuất hiện ở "Mỗi tuần một bài toán "

http://diendantoanho...tây-trung-quốc/

Câu 4:

Rõ ràng mọi số tự nhiên $>2$ nếu muốn là số tốt thì nó phải lẻ (Vì ta thấy nếu nó chẵn thì các $a_i$ phải lẻ và khi đó dễ thấy nếu chọn $k$ lẻ thì vô lý)

Ta chứng minh mọi số tự nhiên lẻ $>2$ đều là số tốt

Thật vậy xét $n$ lẻ $n >2$. Ta chứng minh với mọi $2 \leq k \leq n$ thì đều có thể viết $n= a_1+a_2+...+a_k$ trong đó $(n,a_i)=1$

Thật vậy $k=1$ ta viết $n=(n-1)+1$

Với $x$

Ta sẽ viết $n= (n-2^{x})+2^x$ 

Giờ ta chứng minh $2^x=a_1+a_2+...+a_k$ với mọi $1 \leq k \leq 2^x$ và $a_i$ đều là lũy thừa của $2$ (Điều này hoàn toàn chứng minh dễ dàng bằng quy nạp theo $k$)

Do đó với $2 \leq k \leq 2^x+1$ thì bài toán được chứng minh

Do đó ta chọn $x$ là số lớn nhất thỏa mãn $2^x<n<2^{x+1}$

Khi đó suy ra $2^x >\dfrac{n}{2}$ nên chỉ cần chứng minh nó đúng với $k > \dfrac{n}{2}$

Mặt khác ta cũng viết được $n= 2+2+...+2+1$ nên rõ ràng bằng quy nạp theo $k$ với $k > \dfrac{n}{2}$ thì cũng thỏa mãn

Vậy tất cả các số tốt là $2$ và các số lẻ $>2$

Từ đó ta tính được tổng

Cho $n$ là số nguyên dương. Tập con $S$ của tập $X=\left \{ 1,2,..,n \right \}$ được gọi là "tốt" nếu trung bình cộng của các phần tử thuộc $S$ là một só nguyên. Gọi $T_n$ là số tập con "tốt của $X$. Chứng minh $T_n-n$ chẵn. 

Bài toán quen thuộc sử dụng phương pháp song ánh

Ta bỏ đi $n$ tập con có $1$ phần tử của $T_n$

$T_n-n$ tập "tốt" còn lại chia vào $2$ loại: Tập đó chứa trung bình cộng các phần tử của nó hoặc Tập đó không chứa trung bình cộng các phần tử của nó

Giờ xét tập con của $S=\{a_1,a_2,...,a_k\}$ trong đó trung bình cộng của các phần tử của nó là $a_k$. Khi đó $S \setminus \{a_k\}$ cũng là một tập "tốt" và nó không chứa trung bình cộng các phần tử của nó. Dễ thấy phép biến đổi này là một đơn ánh

Tương tự nếu $S=\{a_1,...,a_k\}$ có trung bình cộng các phần tử của $S$ là $b$ và $b \neq a_i$. Dễ thấy $k<n$ vì $\dfrac{1+2+...+n}{n}$ nếu là số nguyên thì nó cũng nằm trong $X$. Do đó nếu xét $S'$ là hợp của $S$ với $b$ thì $S'$ là một tập con của $X$ và dễ thấy đây cũng là một đơn ánh

Vậy tồn tại một song ánh đi từ $2$ loại tập tốt này vào nhau. Do đó số lượng tập tốt ở mỗi loại này bằng nhau

Do đó $T_n -n  \vdots 2$

Câu 1:

Ta xét 2 trường hợp:

TH1: $5^n \mid a^2$

$k=2\implies p^3=5^n-2$ (vô nghiệm theo modulo $5$)

TH2: $5^n\mid a^2+1$

$n$ lẻ ta có $p^3-1=5^{n}+1\implies v_2(p^3-1)=v_2(5^n+1)\iff v_2(p-1)=v_2(n)>0$

$\implies 2\mid n$ (vô lí)

$TH1$ xét $mod$ $5$ kiểu gì bạn, $TH2$ bạn áp dụng bổ đề nào tính lũy thừa đúng vậy 

                                                                                                           ĐỀ THI CHỌN ĐỘI TUYỂN QUỐC GIA THPT CHUYÊN KHTN VÒNG 1

Câu $2$ : Tìm tất cả đa thức hệ số thực thỏa mãn : 

$$2(P(x)-P(\frac{1}{x}))^{2}+3P(x^{2})P(\frac{1}{x^{2}})=0$$

Thay $x=1$ vào thì $P(1)=0$

Ta thấy $P \equiv 0$ là một nghiệm

Nếu $P$ khác đa thức $0$

Do đó ta có thể đặt $P(x)=(x-1)^nQ(x)$ với $Q(1) \neq 0$

Nếu n lẻ

Ta có: $2\left((x-1)^nQ(x)-\left(\dfrac{1}{x}-1\right)^nQ\left(\dfrac{1}{x}\right)\right)^2=3(x^2-1)^n\left(1-\dfrac{1}{x^2}\right)^nQ(x^2)Q\left(\dfrac{1}{x^2}\right)$

Rút gọn lại: $2\left(x^nQ(x)+Q\left(\dfrac{1}{x}\right)\right)^2=3(x+1)^{2n}Q(x^2)Q\left(\dfrac{1}{x^2}\right)$

Dễ thấy nếu nhân $2$ vế của đẳng thức trên với $x^{2n}$ thì cả $2$ vế đều là đa thức và đẳng thức đúng với mọi $x \neq 1$ nên nó cũng đúng cả với $x=1$ do đó ta được thay $x=1$ và đẳng thức trên 

Suy ra $8Q(1)^2=3.4^n.Q(1)^2$ nên $Q(1)=0$ suy ra  vô lý

Tương tự với $n$ chẵn cũng có điều vô lý

Vậy $P \equiv 0$

Cho điểm $P(m,n)$ với $m,n$ là các số tự nhiên. Giả sử $P$ nằm trên đường thẳng $L:y=px+q$ với $p,q$ là các số tự nhiên. 

Một đường đi từ đỉnh $(0,0)$ đến đỉnh $P$ trong đó mỗi bước đi sẽ theo véctơ $(0,1)$ hoặc $(1,0)$. Chứng minh rằng số các đường đi chỉ cắt $L$ tại một điểm duy nhất là $P$ bằng $\frac{q}{m+n}.\binom{m+n}{m}$

Em nghĩ cái này liên quan đến đường đi ngắn nhất từ điểm $O$ đến $P$ và với mô hình kiểu này thì ta có một bài mẫu khá điển hình là bài $VNTST\ 2003$ và em nghĩ có lẽ bài liên quan đến bài toán đó!

Hôm nay đọc lại bài này mình nghĩ có thể sử dụng $2$ cách để lý giải cho đáp số của bài toán (Cách chứng minh nếu đã biết sẵn đáp án thì quy nạp như cách của JUV sẽ là nhanh gọn nhất  )

Cách 1: Sử dụng phương pháp quỹ đạo (Có trong một chuyên đề của GGTH 2015)

Cách 2: Sử dụng bổ đề xích

Tình cờ hôm nay lang thang trên mạng mình có tìm thấy một chuyên đề rất hay về bổ đề xích và ứng dụng rất đẹp trong các tình huống như bài trên do đó up lại lên diễn đàn để mọi người tham khảo. Bài của Bảo cũng là $1$ bài trong chùm bài tập luyện tập của bổ đề này. Tác giả của tài liệu là thầy Vũ Thế Khôi 

 VTKhoi_cycle-lemma.pdf   140.44K   1319 Số lần tải

Có vẻ như bài 2 từ đoạn Schur xuống AM-GM bạn hơi nhầm thì phải  Tới khúc chỗ shur thì áp dụng trưc tiếp vào vs $q\geq\frac3\$ là đc

$q \geq 3$ làm sao được hả bạn 

Ngày 2:

Bài 3: (Câu này cấu hình lạ nhưng em nghĩ khá rối theo cách làm của em đoạn biến đổi phần b)

a) Gọi $J$ là hình chiếu của $M$ trên $AE$. Do tính đối xứng nên $MN=2MJ$. Do đó chỉ cần chứng minh $\dfrac{MJ}{MR}=\dfrac{EM}{EQ}$

Ta có: $QRJM$ nội tiếp nên $\widehat{JRM}=\widehat{EQM}$. Lại có; $\widehat{RMJ}=\widehat{DEM}$

Do đó $\triangle RMJ \backsim \triangle QEM$ suy ra $\dfrac{MJ}{MR} = \dfrac{EM}{EQ}$ suy ra điều phải chứng minh

b) Kẻ đường cao $AL$ . Gọi $U$ là hình chiếu của $P$ trên $BC$

Ta có: $AL.AO$ đẳng giác nên dễ suy ra $QD$ là phân giác của $\widehat{RQS}$

Mà $DS\perp QS$ nên $DS=DR$ và $R,S$ đối xứng qua $A,E$

Gỉa sử $EN$ cắt $AL$ tại $T$. Do $AE$ là phân giác của $\widehat{TAO}$ và $\widehat{TEO}$ nên dễ dàng suy ra $O,T$ đối xứng qua $A,E$ suy ra $T$ cố định 

Ta chứng minh $PT \perp SM \Leftrightarrow TS^2-TM^2=PS^2-PM^2 $

Mà $PS=PR,TS=OR$( Phép đối xứng trục $AE$) nên chỉ cần chứng minh $OR^2-TM^2=PR^2-PM^2 \Leftrightarrow OM^2+RM^2-TM^2=RU^2-MU^2$

$\Leftrightarrow TM^2-OM^2=RM^2+MU^2-RU^2=(RM-RU)(RM+RU)+MU^2=MU(RM+RU+MU)=2MR.MU$

Chứng minh tương tự phần $a$ ta cũng có: $\dfrac{MJ}{MU}=\dfrac{ME}{PE}$

Do đó $2MU.MR=2MJ^2.\dfrac{EP.EQ}{ME^2}$

Bằng cộng góc dễ dàng chứng minh được $EB$ là tiếp tuyến của $(BPQ)$ nên $2MU.MR=\dfrac{2.MJ^2.EB^2}{ME^2}$ là số cố định nên ta chỉ cần chứng minh đẳng thức trên khi $P \equiv Q$ là tâm nội tiếp của tam giác

Gọi tâm nội tiếp của tam giác là $I$ và tiếp điểm trên $BC$ là $X$

Cần chứng minh: $TM^2-OM^2=2MX^2$

Lại có:

$TM^2-OM^2=TM^2-TD^2+OD^2-OM^2=ML^2-DL^2+DM^2=DM(ML+DL+MD)=2MD.ML$

Do đó chỉ cần chứng minh $MD.ML=MX^2 \Leftrightarrow \dfrac{ML}{MD}=\dfrac{MX^2}{MD^2}$

Mặt khác $\dfrac{ML}{MD}=\dfrac{EA}{ED}$

Và $\dfrac{MX^2}{MD^2}=\dfrac{EI^2}{ED^2}$ nên chỉ cần chứng minh $EI^2=EA.ED$ ( Tính chất quen thuộc)

Vậy ta có đường thẳng qua $P$ vuông góc với $SM$ đi qua điểm $T$ cố định

ĐỀ CHỌN ĐỘI TUYỂN QUỐC GIA TỈNH HÀ TĨNH 2016 - 2017

Ngày 2

Bài 2. (5 điểm) Cho các đa thức $P(x),Q(x),R(x)$ với hệ số thực có bậc tương ứng là $3,2,3$ thỏa mãn đẳng thức $P^2(x)+Q^2(x)=R^2(x),\ \forall x\in \mathbb{R}$. Hỏi đa thức $T(x)=P(x).Q(x).R(x)$ có ít nhất bao nhiêu nghiệm thực (kể cả nghiệm bội).

 

Ngày 2:

Bài 2: Một bài đa thức khá đẹp

TH1: P,Q,R có nghiệm chung là $a$

Khi đó đặt $P(x)=(x-a).P_{1}(x),Q(x)=(x-a).Q_{1}(x),R(x)=(x-a).R_{1}(x)$

Do đó suy ra $P_{1}^2(x)+Q_{1}^2(x)=R_{1}^2(x)$

Gọi dang $2$ đa thức ra ta được: $(ax^2+bx+c)^2+(ex+f)^2=(mx^2+px+q)^2$

Do đó cân bằng hệ số bậc $4$ và bậc $3$ thì ta được $a=m,b=p$

Suy ra $(ax^2+bx+c)^2+(ex+f)^2=(ax^2+bx+p)^2$

Thay $x=\dfrac{-f}{e}$ suy ra  $(ax^2+bx+c)^2=(ax^2+bx+p)^2$ với $x=\dfrac{-f}{e}$

Mặt khác rõ ràng $c \neq p$ nên $ax^2+bx+c+ax^2+bx+p=0$ với $x=\dfrac{-f}{e}$ nên $2ax^2+2bx+p+c$ là phương trình bậc $2$ có nghiệm. Xét $\Delta'=b^2-2(c+p) \geq 0 \Rightarrow (b^2-4c)+(b^2-4p) \geq 0$

Suy ra $ax^2+bx+c$ hoặc $ax^2+bx+p$ có nghiệm 

Do nó là phương trình bậc $2$ nên nếu có nghiệm thì nó sẽ có $2$ nghiệm thực

Do đó $T(x)$ có ít nhất $6$ nghiệm thực (Tính cả nghiệm bội)

TH2: P,Q,R đôi một không có nghiệm chung 

Ta có: $P^2(x)=\left(R(x)-Q(x)\right)\left(R(x)+Q(x)\right)$

Rõ ràng $R(x)-Q(x)$ và $R(x)+Q(x)$ không có nghiệm chung và là $2$ đa thức bậc $3$ nên $P^2(x)$ có ít nhất $2$ nghiệm khác nhau là $2$ nghiệm của $R(x)-Q(x)$ và $R(x)+Q(x)$. Do đó suy ra $P(x)$ có ít nhất $2$ nghiệm khác nhau. Mà $P(x)$ là đa thức bậc $3$ nên nó phải có $3$ nghiệm

Tương tự $Q^2(x)=\left(R(x)+P(x)\right)\left(R(x)-P(x)\right)$

Từ giả thiết thì nếu gọi dang của $P,Q,R$ và cân bằng hệ số bậc $5,6$ thì ta có
$(ax^3+bx^2+cx+d)^2+(ex^2+fx+g)^2=(ax^3+bx^2+mx+n)^2$

Suy ra $P(x)+R(x)$ là đa thức bậc $3$ và $R(x)-P(x)$ là đa thức bậc $1$ nên chúng đều phải có nghiệm và từ $P,Q,R$ đôi một không có nghiệm chung thì rõ ràng $Q^2(x)$ phải có $2$ nghiệm là $2$ nghiệm của $P(x)+R(x)$ và $R(x)-P(x)$. Do đó $Q(x)$ có $2$ nghiệm

Từ đó $P(x)$ có $3$ nghiệm, $Q(x)$ có $2$ nghiệm và $R(x)$ có ít nhất $1$ nghiệm

Tóm lại $T(x)$ có ít nhất $6$ nghiệm

Ta chỉ ra trường hợp dấu $=$ xảy ra như sau :$P(x)=x(x^2+4x+3),Q(x)=2x(x+2),R(x)=x(x^2+4x+5)$

Ngày 1:

Câu 3:

a) Ta có: $A_1A_1' \perp BC \Rightarrow A_1A_1' \perp B_1'C_1'$

Chứng minh tương tự suy ra $A_1A_1',B_1B_1',C_1C_1'$ đồng quy tại $H'$ là trực tâm của tam giác $A_1'B_1'C_1'$

MẶt khác $H'A_1.H'A_1'=H'B_1.H'B_1'=H'C_1.H'C_1'$

Do đó $OH'$ là trục đẳng phương của $3$ đường tròn $(OA_1A_1'),(OB_1B_1'),,(OC_1C_1')$

Do đó $3$ đường tròn $(OA_1A_1'),(OB_1B_1'),,(OC_1C_1')$ cùng đi qua điểm $K$ khác $O$

b) Dễ thấy tam giác $A_1'B_1'C_1'$ là ảnh của tam giác $ABC$ qua phép đối xứng tâm $O$

Do đó $a,b,c$ cũng là độ dài $3$ cạnh của tam giác $A_1'B_1'C_1'$ và $OH=OH'$

Gọi $p'$ là chu vi của tam giác $A_{2}B_{2}C_{2}$ thì dễ thấy $p'=\dfrac{P}{2}$ ( Do tam giác $A_{2}B_2C_2$ là ảnh của tam giác $A_1'B_1'C_1'$ qua phép vị tự tâm $H$ tỉ số $\dfrac{1}{2}$

Do đó ta chỉ cần chứng minh $OK.OH'=\dfrac{abc}{2p'}$

Dễ thấy $OA_1' \perp B_2C_2$ nên $S_{OB_2A_1'C_2}=\dfrac{R.B_2C_2}{2}$ trong đó $R$ là bán kính của $(O)$

Chứng minh tương tự và cộng lại suy ra 

$\dfrac{abc}{4R}=S_{A_1'B_1'C_1'}=\dfrac{R.p'}{2}\Rightarrow \dfrac{abc}{2p'}=R^2$

Lại có: $\widehat{OA_1A_1'}=\widehat{OA_1'A_1}=\widehat{OKA_1}$ nên $OA_1$ là tiếp tuyến của $(H'A_1K)$ suy ra $OK.OH'=OA_1^2=R^2$

Do đó ta có điều phải chứng minh

Câu 4: (Góp $1$ cách khác là đếm truy hồi)

Cho tập $S=\left\{1,2,3,...,n\right\}$. Gọi dãy $(a_1,...,a_n) $ là một dãy đẹp nếu có tính chất $2(a_1+a_2+a_3+...+a_k)\ \vdots\ k$ $\forall k=1,2,...,n$. Khi đó gọi $s_n$ là số dãy đẹp trong các hoán vị của $S$. Ta cần tính $s_{2016}$

Trước hết ta chứng minh $s_n=2s_{n-1}$ $\forall n$ chẵn

Thật vậy ta có: $2(\dfrac{n(n+1)}{2}-a_n) \vdots n-1$

Do đó $2a_{n}\equiv 2 (mod \ n-1)$ hay $a_n \equiv 1 (mod \ n-1)$

Do đó $a_n=1$ hoặc $a_n=n-1$

Rõ ràng  nếu $(a_1,...,a_n) $ là một dãy đẹp và $a_1,...,a_n >1$ thì $(a_1-1,...,a_n-1) $ cũng là một dãy đẹp

Do đó nếu $n$ chẵn thì $s_n=2s_{n-1}$

Với $n$ lẻ và $n>3$. Đặt $n=2k+1 \Rightarrow k>1$ 

Xét tương tự trường hợp $n$ chẵn thì $a_n \equiv 1 (mod \  k)$

Do đó $a_n=1$ hoặc $a_n=n$ hoặc $a_n=k+1$

Tương tự trên  $s_n=2s_{n-1}+t_n$ trong đó $t_n$ là số dãy đẹp có $a_n=k+1$

Giờ ta sẽ xét $a_{n-1}$ 

Ta có: $2\left(\dfrac{n(n+1)}{2}-a_{n-1}-(k+1)\right) \vdots n-2$

Do $n-2$ là số lẻ nên $a_{n-1}+k+1 \equiv 3 (mod \ n-2)$ 

Ta có: $a_{n-1}+k+1 \leq n+k+1< 2(n-2)+3$ (Với $k >1$)

Và $a_{n-1}+k+1>1+1+1=3$ nên suy ra $a_{n-1}+k+1 = (n-2)+3=n+1=2(k+1)$ nên $a_{n-1}=k+1$ suy ra vô lý

Do đó $t_n=0$ với $n$ lẻ và $n>3$

Kết hợp những điều trên suy ra $s_n=2s_{n-1}$ với mọi $n$ nguyên dương và $n>3$

Từ đây dễ dàng suy ra với mọi $n$ nguyên dương và $n>3$ thì $s_n=2^{n-3}s_3$

Mặt khác dễ thấy $s_3=6$ nên $s_n=2^{n-3}.6=3.2^{n-2}$ với mọi $n$ nguyên dương và $n>3$

Vậy $s_{2016}=3.2^{2014}$

Ngày 1:

Câu 1: (khá quen thuộc nhưng mình xét BĐT hơi loằng ngoằng)

a) Xét $f'_{n}(x)=\dfrac{2nx^{2n+1}-(2n+1)x^{2n}+1}{(x-1)^2}$

$f'_n(x)=0 \Leftrightarrow 2nx^{2n+1}-(2n+1)x^{2n}+1=0 (x \neq 1)$

Ta chứng minh $g_{n}(x)=2nx^{2n+1}-(2n+1)x^{2n}+1=0$ có nghiệm duy nhất trên $\mathbb{R}$

Xét $g'_n(x) = 2n(2n+1)x^{2n}-2n(2n+1)x^{2n-1}=0 \Leftrightarrow x^{2n}=x^{2n-1} \Leftrightarrow x=0$ hoặc $x=1$

Do đó với $x<0$ thì $g'_n(x) \neq 0$ do đó $f'_n(x)=0$ có nghiệm duy nhất trên $(-\infty;0)$ 

Mặt khác ta cũng có thể viết : $f'_{n}(x)=2nx^{2n-1}+...+1$ nên rõ ràng với $x\geq 0$ thì  $f'_{n}(x)=2nx^{2n-1}+...+1>0$

Vậy $f'_{n}(x)=0$ có duy nhất một nghiệm

Mặt khác $f_n(x)$ có giá trị nhỏ nhất trên $\mathbb{R}$ nên nó chỉ đạt giá trị nhỏ nhất đó tại một điểm duy nhất 

b) $f'_{n}(x)=2nx^{2n-1}+...+1$

Do đó $f'_{n}(-1)<0$ và $f'_{n}(0)>0$ nên rõ ràng $(s_n)$ bị chặn giữa $-1$ và $0$

Ta chứng minh $(s_n)$ là dãy giảm

Từ phần $(a)$ dễ suy ra $f'_{n}(x)$ đồng biến trên $(-\infty;0)$

Do đó chỉ cần chứng minh $f'_{n+1}(s_n) > f'_{n+1}(s_{n+1})=0$

Do đó ta cần chứng minh $2(n+1)s_{n}^{2n+1}+(2n+1)s_{n}^{2n}>0$ hay $s_n>\dfrac{-(2n+1)}{2(n+1)}$

Hay cần chứng minh $f_n(\dfrac{-(2n+1)}{2(n+1)}) <0$

Bằng cách ghép lần lượt $2nx^{2n-1}+(2n-1)x^{2n-2} <0$ và tương tự thì ta dễ dàng có điều phải chứng minh 

Do đó $s_{n}$ giảm và bị chặn nên ta có điều phải chứng minh

Câu 2: (Nhiều khả năng bài này chế từ một bài trong Old and new)

Áp dụng bất đẳng thức $AM-GM$ thì dễ có $a^5b^5(a^5+b^5+1+1+1)\geq 5a^6b^6$

Chứng minh tương tự và đặt $a^5=x,b^5=y,c^5=z$ thì $x+y+z=3$

Ta có: $5(a^6b^6+b^6c^6+c^6a^6) \leq xy(x+y+3)+yz(y+z+3)+zx(z+x+3)=2pq-3r$ với $p=x+y+z,q=xy+yz+zx,r=xyz$

Áp dụng bất đẳng thức Schur ta thu được: $27+9r\geq 4pq \Leftrightarrow 2pq-\dfrac{9r}{2} \leq \dfrac{27}{2} $

Áp dụng bất đẳng thức $AM-GM$ ta thu được $r \leq 3 \Leftrightarrow \dfrac{r}{2} \leq \dfrac{3}{2}$

Suy ra $5(a^6b^6+b^6c^6+c^6a^6) \leq 15 \Rightarrow a^6b^6+b^6c^6+c^6a^6 \leq 3$

Dấu "=" xảy ra khi và chỉ khi $a=b=c=1$

Câu 4 ngày 1 liệu có vấn đề gì không nhỉ sao nó đúng với $k=0$ được

Bài 5(3 điểm):

Có bao nhiêu số tự nhiên có $50$ chữ số,chia hết cho $9$,trong đó có đúng $10$ chữ số $9$ và giữa hai chữ số $9$ bất kì có ít nhất hai chữ số

 

Có mạng phát là phải xem ngay mấy đề thi HSG Tỉnh mới được 

Bỏ đi 10 chữ số 9 thì ta nhận được một dãy 40 chữ số

TH1: Số 9 là chữ số đầu tiên của số đó

Khi đó dãy gồm 40 chữ số kia là tùy ý( Tổng 40 chữ số đó chia hết cho 9)

Do đó số dãy gồm 40 chữ số như vậy là tổng các hạng tử ứng với lũy thừa chia hết cho $9$ của đa thức $P(x)=(1+x+x^2+...+x^9)^{40}$

Áp dụng định lý $RUF$ ta có thể dễ dàng tính được số dãy như vậy là $\dfrac{10^{40}+8}{9}$(Thực ra có thể không cần dùng định lý $RUF$ mà xét lần lượt xem dãy gồm $40$ chữ số kia thực chất tạo bởi số có mấy chữ số bằng cách bỏ đi dãy các số $0$ đứng đầu dãy)

Giờ ta xem 1 dãy như vậy tạo được bao nhiêu số thỏa mãn đề bài: 

Theo bài toán chia kẹo $Euler$ nó ứng với số nghiệm của phương trình: $x_1+x_2+...+x_9=40$ và $x_1,x_2,...,x_8 \geq 2, x_9 \geq 0$ 

Chúng tương đương với số nghiệm nguyên không âm của phương trình :$x_1+x_2+...+x_9=24$ và là $C^{8}_{32}$

TH2: Số 9 không là chữ số đầu tiên của số đó

Khi đó dãy 40 chữ số kia có số đầu khác $0$ hay nói cách khác nó là một số có $39$ chữ số  ( Tổng 40 chữ số đó chia hết cho 9)

Khi đó số số như vậy sẽ là $10^{39}$ 

Giờ ta xem 1 dãy như vậy tạo được bao nhiêu số thỏa mãn đề bài: 

Theo bài toán chia kẹo $Euler$ nó ứng với số nghiệm của phương trình: $x_1+x_2+...+x_9+x_10=40$ và $x_2,x_2,...,x_9 \geq 2, x_9 \geq 0,x_1 \geq 1$ 

Chúng tương đương với số nghiệm nguyên không âm của phương trình :$x_1+x_2+...+x_10=23$ và là $C^{9}_{32}$

Vậy số số thỏa mãn là $\dfrac{C^{8}_{32}\left(10^{40}+8\right)}{9}+10^{39}.C^{9}_{32}$