Tìm kiếm
Nữ
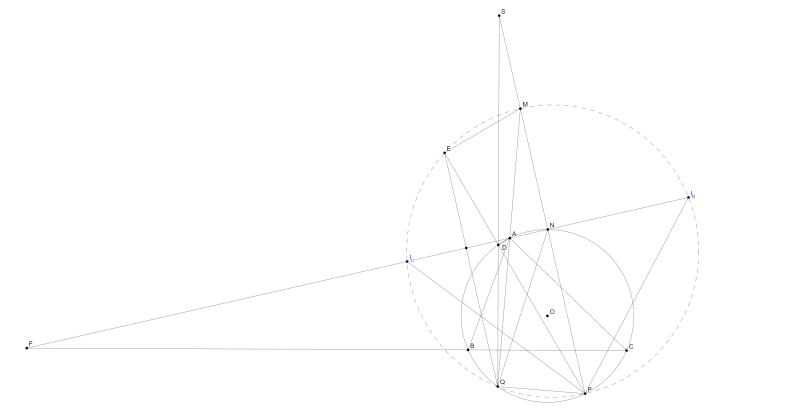
Gửi bởi Cho $\Delta ABC$ nội tiếp đường tròn $(O). O_a, O_b, O_c$ lần lượt là tâm của $(OBC), (OCA), (OAB). XYZ$ là tam giác Cevian của $O$ đối với $\Delta O_aO_bO_c. P$ là trực tâm $\Delta XYZ.$ Chứng minh $OP$ đi qua điểm Kosnita của $\Delta ABC.$
Định nghĩa điểm Kosnita: https://vi.wikipedia...Định_lý_Kosnita
Ta đưa về mô hình tâm nội tiếp bởi vì $O_aO$ là phân giác góc $\angle O_bO_aO_c$
Đưa về bài toán sau:
Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. $AI,BI,CI$ giao $BC,AC,AB$ tại $X,Y,Z$. $G$ là trực tâm của $\Delta XYZ$. $O_a,O_b,O_c$ là điểm đối xứng của $I$ qua $BC,AC,AB$. Chứng minh $IG$ đi qua điểm đồng quy của $AO_a,BO_b,CO_c$
Bổ đề: Cho $\Delta ABC$, điểm $P$ bất kỳ trong mặt phẳng. $AP,BP,CP$ giao $BC,AC,AB$ tại $D,E,F$. $Q$ bất kỳ trên mặt phẳng. $DQ,EQ,FQ$ giao $EF,FD,DE$ tại $D_1,E_1,F_1$. $PD_1,PE_1,PF_1$ giao $BC,AC,AB$ tại $A_1,B_1,C_1$. Chứng minh rằng $AA_1,BB_1,CC_1$ đồng quy trên $PQ$
Chứng minh:
Gọi các điểm như hình vẽ
Ta có $F(PI,AJ)=F(PX,C_1B_1)=P(FX,C_1B_1)=P(FX,YZ)$
Mà $F(PI,AJ)=F(CE,AB_1)=F(EC,B_1A)=P(EF,E_1D)=E(PF,E_1D)=E(PF,YF_1)=F(PE,YF_1)=F(PX,YZ$
Nên $X,Y,Z$ thẳng hàng
Dùng Desargue cho $\Delta QEF$ và $\Delta PC_1B_1$ nên $P,Q,G$ thẳng hàng
Áp dụng định lý Pappus cho bộ $(B,C_1,F)$ và bộ $(C,B_1,E)$ nên $P,H,G$ thẳng hàng
Suy ra $H,P,Q$ thẳng hàng
DPCM
Quay lại bài toán
Gọi $A_1,A_2,G_x$ là giao của $AO_a,AX,XG$ và $BC,YZ,YZ$
Theo hàng điểm có $YZ$ là phân giác $\angle AG_xI$
Và $A_1A_2$ vuông góc $BC$
Nên $\angle A_2G_xA_1=\angle A_2XA_1=\angle AG_xA_2=\angle A_2G_xI$
Nên $A_1,G_x,I$ thẳng hàng
Áp dụng bổ đề có dpcm
- DaiphongLT yêu thích
