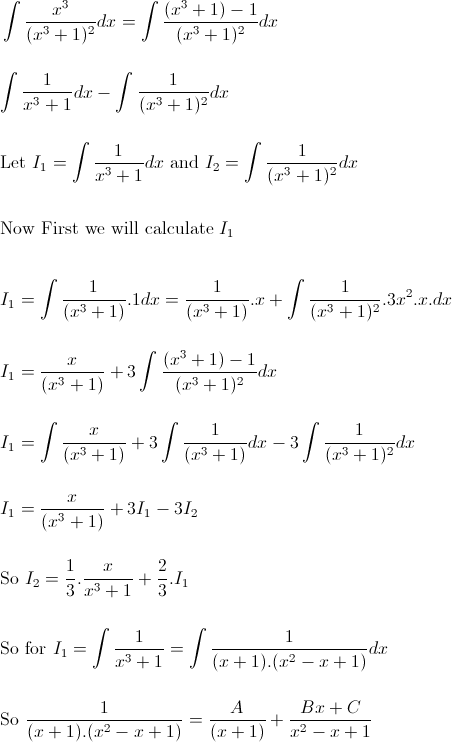stuart clark

Cho $x,y,z,t>0,$ Tim Min $x^5+3\sqrt{3}\; y^5+\sqrt{3}z^5+t^5-15xyzt$

Let $\displaystyle I = \int^{4}_{2}\frac{\sqrt{\ln(9-x)}}{\sqrt{\ln(9-x)}+\sqrt{\ln(x+3)}}dx\cdots \cdots (1)$

 

Using $\displaystyle \int^{b}_{a}f(x)dx = \int^{b}_{a}f(a+b-x)dx$

 

So $\displaystyle I = \int^{4}_{2}\frac{\sqrt{\ln(9-(2+4-x))}}{\sqrt{\ln(9-(2+4-x))}+\sqrt{\ln(2+4-x+3)}}dx$

 

So $\displaystyle I = \int^{4}_{2}\frac{\sqrt{\ln(3+x)}}{\sqrt{\ln(9-x)}+\sqrt{\ln(x+3)}}dx\cdots \cdots (2)$

 

So $\displaystyle 2I = \int^{4}_{2}1 dx = 2\Rightarrow I = 1$

Cho  $A,B,C>0$ thoả mãn $A+B+C = \pi\;, \sin^2 A+\sin^2 B+\sin^2 C = 2,$ Tim Min: $\sin A \sin B+\sin B\sin C+\sin C\sin A$

Cho $x,y,z >0,$ Tìm min:$\displaystyle P=(8x^2+y^2+z^2)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2$

$\bf{A.M\geq G.M}$

 

$\displaystyle \frac{4x^2+4x^2+y^2+z^2}{4}\geq \sqrt[4]{4x^2\cdot 4x^2\cdot y^2\cdot z^2}\Rightarrow 8x^2+y^2+z^2\geq 4\sqrt[4]{16x^4\cdot y^2\cdot z^2}$

 

$\displaystyle \left(\frac{1}{2x}+\frac{1}{2x}+\frac{1}{2x}+\frac{1}{2x}\right)\geq 4\sqrt[4]{\frac{1}{2x}\cdot \frac{1}{2x}\cdot \frac{1}{y}\cdot \frac{1}{z}}$

 

$\displaystyle \left(8x^2+y^2+z^2\right)\cdot \left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2\geq 64$

 

Dấu bằng xảy ra khi và chỉ khi $2x=y=z.$

$$I_{n} = \int_{0}^{\frac{\pi}{2}}\sin^{n}xdx =  \int_{0}^{\frac{\pi}{2}}\sin^{n-1}x\cdot \sin x dx$$

 

$$I_{n} = -\left[\sin^{n-1}x\cos x\right]_{0}^{\frac{\pi}{2}}+(n-1)\int_{0}^{\frac{\pi}{2}}\sin^{n-2}\cos^2 x$$

 

$$I_{n} = (n-1)\int_{0}^{\frac{\pi}{2}}\sin^{n-2}x(1-\sin^2 x)dx = (n-1)I_{n-2}-(n-1)I_{n}$$

 

$$I_{n} = \frac{n-1}{n}I_{n-2}$$

$$I = \int \left(1+x+\frac{1}{x}\right)e^{x-\frac{1}{x}}dx = \int \left(1+\frac{1}{x}+\frac{1}{x^2}\right)e^{x-\frac{1}{x}+\ln(x)}dx$$

 

$x-\frac{1}{x}+\ln(x) = t\;,$ Th $\displaystyle \left(1+\frac{1}{x}+\frac{1}{x^2}\right)dx = dt$

 

$$ I = \int e^tdt = e^t+\mathcal{C} = e^{x-\frac{1}{x}+\ln(x)}+\mathcal{C} = xe^{\left(x-\frac{1}{x}\right)}+\mathcal{C}$$

for (1)......

$(1)\;\; a,b,c,d\in\mathbb{R^{+}}\;\;,a+b+c=1$. Then prove that

$\displaystyle \left(a+\dfrac{1}{b}\right).\left(b+\dfrac{1}{c}\right).\left(c+\dfrac{1}{a}\right)\geq \left(\dfrac{10}{3}\right)^3$

$(2)\;\; a,b,c\in \left[0,\infty\right)$. Then prove that

$\displaystyle \left(a-\dfrac{1}{b}\right). \left(b-\dfrac{1}{c}\right). \left(c-\dfrac{1}{a}\right)\geq \left(a-\dfrac{1}{a}\right). \left(b-\dfrac{1}{b}\right). \left(c-\dfrac{1}{c}\right)$

max. and min. value of $f(x) = \sin x+\cos x +\sin x.\cos x$

$\int_{0}^{\dfrac{\pi}{3}}\dfrac{x.\sin^4 x}{\cos^2 x}dx$

$\int_{0}^{\dfrac{\pi}{3}}\dfrac{x.\left(1-\cos^2 x\right)^2}{\cos^2 x}dx = \int_{0}^{\dfrac{\pi}{3}}\dfrac{x+x.\cos^4 x-2x.\cos^2 x}{\cos^2 x}dx$

$\int_{0}^{\dfrac{\pi}{3}}x.\sec^2 xdx+\int_{0}^{\dfrac{\pi}{3}}x.\cos^2 xdx-\int_{0}^{\dfrac{\pi}{3}}2xdx$

$\int_{0}^{\dfrac{\pi}{3}}x.\sec^2 xdx+\dfrac{1}{2}.\int_{0}^{\dfrac{\pi}{3}}x.\left(1+\cos (2x)\right)dx-\int_{0}^{\dfrac{\pi}{3}}2xdx$

use Integration by distribution.

$=x.\tan x\Bigg|_{0}^{\dfrac{\pi}{3}} -\ln(\sec x)\Bigg|_{0}^{\dfrac{\pi}{3}}+\dfrac{1}{4}.x^2\Bigg|_{0}^{\dfrac{\pi}{3}}+\dfrac{1}{4}.x\sin (2x)\Bigg|_{0}^{\dfrac{\pi}{3}}+\dfrac{1}{8}\cos(2x)\Bigg|_{0}^{\dfrac{\pi}{3}}-x^2\Bigg|_{0}^{\dfrac{\pi}{3}}$

$=\dfrac{\pi}{3}.\tan \left(\dfrac{\pi}{3}\right)-\ln(2)+\dfrac{1}{4}.\sin \left(\dfrac{2\pi}{3}\right)+\dfrac{1}{8}\left(\cos \left(\dfrac{2\pi}{3}\right)-\cos(0)\right)-\dfrac{\pi^2}{9}$

$=\dfrac{\pi}{3\sqrt{3}}-\ln(2)+\dfrac{\sqrt{3}}{2}-\dfrac{3}{16}-\dfrac{\pi^2}{9}$