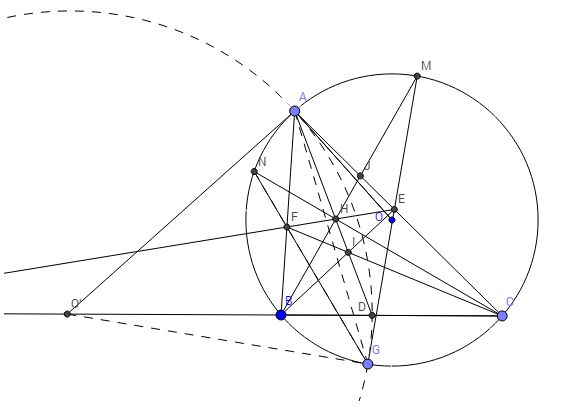
Cho tam giác $ABC$ có 3 đường cao $AD,BE,CF$ đồng quy tại $H$.Gọi $M$ là giao điểm $FD$ và $BH$,$N$ là giao điểm $DE$ và $HC$.$I$ là tâm đường tròn Euler.Cm:$MN$ vuông góc $AI$

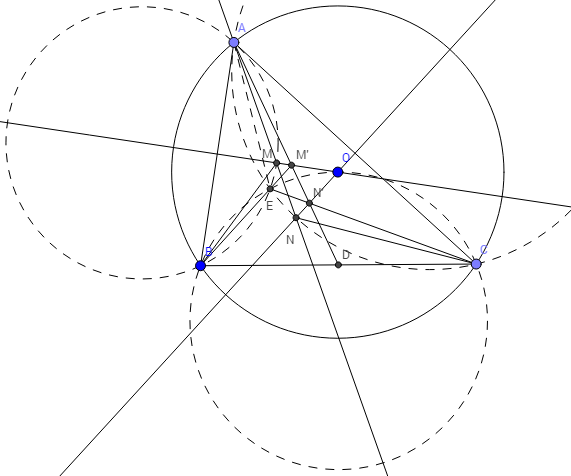
Gọi $(K)$ là đường tròn ngoại tiếp tam giác $BHC$. Có $A$ là trực tâm tam giác $BHC$, đường tròn $(E)$ là đường tròn Euler của tam giác $HBC$ nên $I$ là trung điểm $AK$/

 

Ta chứn mình $MN$ vuông góc với $EI$

Do 4 điểm $B,F,H,D$ đồng viên, $H,E,C,D$ đồng viên nên

$$P(M/(K))=MB.MH=MD.MF$$

$$P(N/(K))=NH.NC=ND.NE$$

Suy ra $M,N$ có cùng phương tích với $(E)$ và $(K)$ nên $MN$ là trục đẳng phương do đó có đpcm!

 

(hình vẽ thì mình không biết dùng thế nào.

Đây là đề thi hsg lớp 10 trường THPT chuyên Nguyễn Trãi chọn đội tuyển thi Olympic Duyên Hải năm 2015)

Thực ra bài toán này chính là một bổ đề có nhiều ứng dụng mà thầy Hùng đã đề cập đến trong này

Bài 3 ngày 1​

Ta có:

$3(a+b+c)\geq (a^2+b^2+c^2)(a+b+c)=(a^3+b^2a)+(b^3+c^2b)+(c^3+a^2c)+(a^2b+b^2c+c^2a)\geq 3(a^2b+b^2a+c^2a)$

Ta đi chứng minh: $(a+b+c)(a+b+c-abc)\geq 2(a+b+c)\Leftrightarrow a+b+c-abc-2\geq 0$

Giả sử $a\geq b\geq c$. Từ điều kiện $a^2+b^2+c^2\leq 3\Rightarrow a+b+c\leq 3\Rightarrow c\leq 1, a\geq 1$

$\Rightarrow b^2+c^2\leq 2\Rightarrow bc\leq 1$

Mà $c^2\leq 1\Rightarrow b^2\geq 1$

Đặt: $f(a;b;c)=a+b+c-abc-2$

Xét: $f(a;b;c)-f(1;b;c)=(a-1)(1-bc)\geq 0$

Mà: $f(1;b;c)=(b-1)(1-c)\geq 0$

Từ đó ta có: $a+b+c-abc-2\geq 0$

Vậy ta có đpcm

Dấu $"="$ xảy ra khi và chỉ khi $a=b=c=1$

Ta có: $3\geq a^2+b^2+c^2$ nên $3\geq a+b+c$ và $abc\leq 1$.

Ta nhớ đến BĐT quen thuộc sau: $a^2b+b^2c+c^2a+abc\leq \frac{4}{27}(a+b+c)^3$

Đặt $p=a+b+c;q=ab+bc+ca;r=abc$, ta chỉ cần chứng minh:

$p^2-pr+2r\geq \frac{8}{27}p^3$

$\Leftrightarrow 27p^2-27pr+54r\geq 8p^3$  

Mặt khác vì $3\geq p$ nên $8p^3\leq 24p^2$ dẫn đến $27p^2-8p^3\geq 3p^2$

Ta chứng minh BĐT: $3p^2+54r\geq 27pr$ hay $p^2+18r\geq 9pr$

$\Leftrightarrow p^2\geq 9pr-18r$.  $(1)$

Lại có: $9pr\leq 27r$ nên $9pr-18r\leq 9r$.  $(2)$

Và $p^2\geq 9\sqrt[3]{(abc)^2}\geq 9abc$ (vì $abc\leq 1$)   $(3)$

Từ $(1),(2)$ và $(3)$ ta có điều phải chứng minh.

Dấu bằng xảy ra tại $a=b=c=1$

câu số:

$(2x-y)(4x^2+2xy+y^2-1)=6x^3;(2x-y;y)=1\rightarrow 2x-1=1;2;3;6$

Câu hình ý a khá đơn giản, ý b em nghĩ sử dụng đường đối trung chỉ cần cm: $A,H,X$ thẳng hàng với $X$ là trđ BC.... ?

Thực ra câu b hình để ý rằng $I$ nằm trên trục đẳng phương của hai đường tròn $(AMB)$ và $(ANC)$. Ta sẽ gọi giao điểm của 2 đường tròn này là $E$ thì chỉ cần chứng minh $AE$ là đường đối trung với $AX$ ($X$ là trung điểm của $BC$).

Gọi $M',N'$ lần lượt là giao điểm của $OM,ON$ với $AX$, $BM'\cap CN'=E'$.

Mặt khác: $\widehat{AEB}=\widehat{AEC}=180-\widehat{BAC}$

$\frac{AB}{AE'}=\frac{\sin AE'B}{\sin ABE'}$

$\frac{AC}{AE'}=\frac{\sin AE'C}{\sin ACE'}$

$\frac{AB}{AC}=\frac{\sin N'AC}{\sin M'AB}=\frac{\sin E'CA}{\sin E'BA}$

Do đó: $\widehat{AE'B}=\widehat{AE'C}$

Mặt khác ta chứng minh được $BE'OC$ nội tiếp (bằng cộng góc) nên $\widehat{AE'B}=\widehat{AE'C}=180-\widehat{BAC}$

Do đó $E\equiv E'$ hay $B,E,M'$ thẳng hàng và $C,E,N'$ thẳng hàng.

Như vậy ta có: $\widehat{EAB}+\widehat{EBA}=\widehat{BAC}=\widehat{BAD}+\widehat{DAC}$

Dẫn đến $\widehat{EAB}=\widehat{DAC}$

Vậy $AE$ là đường đối trung của tam giác $ABC$ nên $A,E,S$ thẳng hàng. Suy ra ĐPCM 

Spoiler

Ngoài cách này mình còn 1 cách giải bằng hình học phẳng thuần túy nhưng nhác gõ quá

giai thich cho minh cho nay dc k

 

 

Gọi $A_1$ là phần tử có nhiều nhất trong $64$ tập con và $a_1$ là số tập con chứa $A_1$, ta có:

$a_1\geq \frac{64.1008}{2016}=32$

Nếu gọi $A_1$ là phần tử nhiều nhất trong $64$ tập con và $a_1$ là số tập con chứa $A_1$ thì vì mỗi tập con có chứa ít nhất $1008$ phần tử nên $64$ tập con phải chứa $64.1008$ phần tử nếu tính cả phần lặp của các phần tử, nhưng vì $A_1$ là phần tử có các tập con chứa nhiều nhất nên tối thiểu số lần xuất hiện của nó trong các tập con phải lớn hơn tất thảy $2015$ phần tử còn lại. Do đó mới có BĐT $a_1\geq \frac{64.1008}{2016}=32$

Nếu bây giờ bạn cho $a_1< 32$ thì vì $a_1$ là lớn nhất trong tất cả $a_i$ với $i=1,2,...,2016$ nên $64$ tập con chỉ chứa $<32.2016=64.1008$ phần tử dẫn đến điều vô lý  

 

 

Bài 5 (4 điểm)

 

        Cho tập hợp $X$ có $2016$ phần tử.Chọn ra $64$ tập con $X_1,X_2,...,X_64$ của tập $X$ {mỗi tập con đều chứa nhiều hơn $1008$ phần tử} . Chứng minh rằng:tồn tại tập con $A$ của $X$ có số phần tử không vượt quá $6$ mà $A\cap X,\neq \oslash,i=\overline{1,64}$ 

 

HẾT

 

Chém nốt câu tổ:

Gọi $A_1$ là phần tử có nhiều nhất trong $64$ tập con và $a_1$ là số tập con chứa $A_1$, ta có:

$a_1\geq \frac{64.1008}{2016}=32$

Chọn $A_1$ và loại đi $a_1$ tập con chứa $A_1$, gọi $A_2$ với $a_2$ tương tự trên, ta có:

$a_2\geq \frac{(64-a_1).1008}{2015}$

Khi đó: $a_1+a_2\geq a_1+\frac{(64-a_1).1008}{2015}=\frac{64.1008+1007a_1}{2015}>48$ nên $a_1+a_2\geq 49$

$a_3\geq \frac{(64-a_1-a_2).1008}{2014}$ nên $a_1+a_2+a_3>56$ nên $a_1+a_2+a_3\geq 57$

Tương tự:

$a_1+a_2+a_3+a_4\geq 61$

$a_1+a_2+a_3+a_4+a_5\geq 63$

$a_1+a_2+a_3+a_4+a_5+a_6\geq 64$

Chọn các phần tử $A_1,A_2,A_3,A_4,A_5,A_6$ ta thu được điều phải chứng minh

Câu bất đẳng thức

Đặt $(a;b;c) -> (\frac{1}{a}; \frac{1}{b}; \frac{1}{c} $

Ta được $ab+bc+ca= 1 $

Ta có bđt được viết lại

$\frac{(a-b)^2}{a} + \frac{(b-c)^2}{b} + \frac{(a-c)^2}{c} \geq \frac{1}{2}(\sum  (a-b)^2)(1-\frac{1}{a+b+c+\sqrt{3}})$

Tới đây.

C1:  Chứng minh tựa như SOS

C2: Sử dụng bđt C-S cho VT rồi giả sử $b$ nằm giữa $a$ và $c$

Mình có cách "sơ cấp" hơn  

Đặt $x=\frac{1}{a};y=\frac{1}{b};z=\frac{1}{c}$ thì từ giả thiết ta được $xy+yz+xz=1$.

Yêu cầu bài toán viết lại thành:

$3+\sum \frac{x^2}{y}\geq (x+y+z)^2+\sqrt{3}$

Mặt khác: $\sum \frac{x^2}{y}=(\sum xy) (\sum \frac{x^2}{y})\geq (x+y+z)(x^2+y^2+z^2)$ nên ta chỉ cần chứng minh:

$p^3-p^2-2p+3-\sqrt{3}\geq 0$ với $p=x+y+z\geq \sqrt{3}$.

Chứng minh được BĐT này đúng  

Thực chất thì câu 2 của bài này là hệ quả của định lý $Thébault$, đúng hơn là chỉ cần áp dụng 2 lần bổ đề $Sawayama$ (đọc đề cũng đủ hiểu )

Cụ thể thì nó phát biểu như sau:

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $D$ là một điểm nằm trên cạnh $BC$. Đường tròn tâm $Q$ tiếp xúc với hai đoạn $AD, BD$ và tiếp xúc trong với $(O)$. Đường tròn tâm $P$ tiếp xúc với hai đoạn $AD, CD$ và tiếp xúc trong với $(O)$. Gọi $I$ là tâm đường tròn nội tiếp tam giác $ABC$ thì $P,I,Q$ thẳng hàng

Chứng minh có dùng bổ đề $Sawayama$.

Áp dụng vào bài toán thì đơn giản rồi

Cho tam giác $ABC$. Dựng ngoài tam giác 2 tam giác cân đồng dạng $ABP , ACQ$ đều cân ở $A$.

$CP$ cắt $BQ$ tại $R. O$ là tâm $(BRC)$

Chứng minh: $AO$ vuông góc $PQ$

Trước tiên ta dễ dàng chứng minh được $\Delta ACP=\Delta AQB$ (c-g-c)

Từ đó suy ra các tứ giác $APBR, AQCR$ nội tiếp.

Bây giờ gọi $O_1,O_2$ lần lượt là tâm các đường tròn ngoại tiếp các tứ giác ở trên.

Dễ thấy $OO_1\perp RQ$ và $OO_2\perp RP$.

Theo định lý $Carnot$ thì bài toán sẽ được chứng minh nếu ta chỉ ra được:

$AP^2-AQ^2+O_1Q^2-O_1R^2+O_2R^2-O_2P^2=0$

Chứng minh đẳng thức này khá đơn giản nếu sử dụng công cụ $Vector$

Bài 3 (4,0 điểm).

 

1. Một trường THPT có 20 học sinh tiêu biểu, trong đó có 5 học sinh lớp 10, 6 học sinh lớp 11 và 9 học sinh lớp 12. Ban chấp hành đoàn trường chọn ngẫu nhiên 8 học sinh từ 20 học sinh đó để đi dự trại hè của thành phố. Tính xác suất để ban chấp hành đoàn trường chọn được 8 học sinh sao cho mỗi khối có ít nhất một học sinh.

 

 

Gọi $A,B,C$ là tập hợp số phần tử $8$ học sinh không thuộc khối $10,11,12$.

Ta tính được: $|A|=C^8_{15}$; $|B|=C^8_{14}$; $|C|=C^8_{11}$.

Khi đó: $|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

mà $|A\cap B\cap C|=0$ (vì không thể có trường hợp 8 học sinh không thuộc khối nào).

$|A\cap B|=C^8_9$; $|A\cap C|=|B\cap C|=0$

Do đó $|A\cup B\cup C|=C^8_{15}+C^8_{14}+C^8_{11}-C^8_9=9594$

Nên số cách chọn 8 học sinh sao cho mỗi khối có ít nhất 1 học sinh là: $C^8_{20}-9594=116376$

Từ đó tính ra xác suất.

Câu 5 vòng 1 chú ý đánh giá từ phương trình 1 có $x^2+y^2\geq \sqrt{x}+\sqrt{y}$ (tách vế trái ra dùng C-S)

Còn ở PT 2 thì chứng minh $\sqrt{x}+\sqrt{y}\geq x^2+y^2$

Câu 4 vòng 2:

Đặt 100 số đó là $x_1,x_2,...,x_100$, đặt $y_1=x_1;y_2=x_1-1;...;y_{100}=x_{100}-99$ thì $1\leq y_1<y_2<...<y_{100}\leq 1917$

Do đó số cách chọn là $1917C100$

Câu hình thì câu a đơn giản, câu b chứng minh $JTIS$ nội tiếp (biến đổi góc hoặc cạnh, tùy)

Hình câu a dùng tính chất đường tròn A-Apollonius và hàng điểm điều hòa là ra ạ:

Gọi $(O')$ là đường tròn đi qua $A,D$ và tiếp xúc với $OA$ thì $(O')$ trực giao với $(O)$ nên $O'$ thuộc $BC$, do đó $O'A^2=O'B.O'C=OG^2$ nên $OG$ là tiếp tuyến của $(O)$ hay tứ giác $ABGC$ điều hòa, gọi $H'$ là giao của $EF$ và $AD$, $K$ là giao của $EF$ và $BC$, theo một tính chất quen thuộc thì $(KBO'C)=-1$ nên $F(KBO'C)=(H'DAB)=B(H'DAB)=(JCAE)=-1$ (với $J$ là giao của $BH'$ với $AC$=> $M(JCAE)=-1$ mà $M(BCAG)=-1$ nên $B,J,M$ thẳng hàng, tương tự ta được $H\equiv H'$ nên $H$ nằm trên $AD$ do đó $AH$ đi qua điểm chính giữa cung $BC$ cố định.

Cho $\triangle{ABC},P$ là điểm bất kì. $PA,PB,PC$ cắt đường tròn ngoại tiếp $(O)$ của tam giác $ABC$ tại $A_1,B_1,C_1$. Gọi $A_2,B_2,C_2$ là các điểm đối xứng với $A_1,B_1,C_1$ qua trung điểm $BC,AC,AB$. Chứng minh $H,A_2,B_2,C_2$ cùng thuộc một đường tròn . Biết rằng $H$ là trực tâm của tam giác $ABC$ 

Đây chính xác là Đường tròn Hagge, câu T12 trên báo THTT tháng 12 cũng là hệ quả của đường tròn này !

1. Cho $x,y,z \in \mathbb{R}$, $x\neq y\neq z$.

CMR: $\frac{xy}{(x-y)^2}+\frac{yz}{(y-z)^2}+\frac{zx}{(z-x)^2}\geq \frac{-1}{4}$

2. Tim GTNN cua P = $x+\frac{11}{2x}+\sqrt{4.(1+\frac{7}{x^2})}$ (x>0)

Bài 1:

BĐT tương đương: $\sum \left [ 1+\frac{4ab}{(a-b)^2} \right ]\geq 2<=>\sum (\frac{a+b}{a-b})^2\geq 2$

Đặt $x=\frac{a+b}{a-b};y=\frac{b+c}{b-c};z=\frac{c+a}{c-a}$ ta có:

$(x+1)(y+1)(z+1)=(x-1)(y-1)(z-1)$

Suy ra $xy+yz+xz=-1$

Mặt khác: $x^2+y^2+z^2\geq -2(xy+yz+xz)=2$ hay chính là ĐPCM

Mình xin đăng lại 2 bài toán sau của thầy Hùng để mọi người cùng thảo luận và đưa lời giải. Link bài viết của thầy Hùng: http://analgeomatica...quan-trong.html

Bài 1: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, tâm nội tiếp $(I)$. $IB,IC$ lần lượt cắt $(O)$ tại $M,N$ khác $B,C$. $P,Q$ lần lượt nằm trên tia đối tia $BC,CB$ sao cho $BP=BA$, $CQ = CA$. $K, L$ lần lượt là tâm ngoại tiếp tam giác $NBP, MCQ$. $BL$ cắt $CK$ tại $D$. Đường tròn bàng tiếp góc $A$ là $(I_a)$ cắt $(O)$ tại $S, T$. Chứng minh rằng $AD \perp ST.$

Bài 2: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Phân giác góc $B, C$ cắt $(O)$ tại $E, F$ khác $B, C$. $P, Q$ thuộc tia đối tia $BC, CB$ sao cho $BP= BA, CQ = CA$. Từ $A$ vẽ tiếp tuyến $AX, AY$ tới đường tròn ngoại tiếp tam giác $BFP$ và tiếp tuyến $AZ, AT$ tới đường tròn ngoại tiếp tam giác $CEQ$. Gọi $M, N$ là trung điểm $XY, ZT$. Gọi đường tròn ngoại tiếp tam giác $ACM$ và $ABN$ cắt nhau tại $R$ khác $A$. Đường tròn $(K)$ tiếp xúc $AB, AC$ và tiếp xúc trong $(O)$ cắt $BC$ tại $G, H$. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $AGH$ nằm trên $AR.$

Bài 1:  Về một bài toán hay (1).pdf   330.69KB   929 downloads

Ở đây cần lưu ý có thể dùng lượng giác giúp chứng minh $\widehat{KAB}=\widehat{CAL}$ trở nên ngắn gọn hơn nhiều so với cách trên.

Cho $a, b, c, d, e > 0$ thỏa mãn điều kiện $a + b + c + d + e = 4$. Tìm GTNN của biểu thức $P = \frac{(a + b + c + d)(a + b + c)(a + b)}{abcde}$

Ta có:$16P=\frac{(a+b+c+d+e)^2(a+b+c+d)(a+b+c)(a+b)}{abcde}\geq \frac{4e(a+b+c+d)^2(a+b+c)(a+b)}{abcde}$

$\geq \frac{16d(a+b+c)^2(a+b)}{abcd}\geq \frac{64c(a+b)^2}{abc}\geq 4^4$

Do đó: $P\geq 16$

1.Cho $a,b,c$ là các số thực dương sao cho $abc=1$.

CMR: $\frac{a+3}{(a+1)^2}+\frac{b+3}{(b+1)^2}+\frac{c+3}{(c+1)^2} \geq 3$

2.Cho $a,b,c$ là các số thực dương thỏa mãn $a+b+c=3$.

CMR: $\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2} \geq a^2+b^2+c^2$

 

1. Giả sử $c=min(a,b,c)$ thì $ab\geq 1$

Ta có:$\frac{a+3}{(a+1)^2}+\frac{b+3}{(b+1)^2}=\frac{1}{a+1}+\frac{1}{b+1}+2.\left [ \frac{1}{(a+1)^2} +\frac{1}{(b+1)^2}\right ]\geq \frac{2}{1+\sqrt{ab}}+\frac{2}{1+ab}$

Từ đó thay $ab=\frac{1}{c}$ vào rồi biến đổi tương đương ta được ĐPCM

2.BĐT tương đương:

$\sum b^2c^2\geq a^2b^2c^2(a^2+b^2+c^2)$

Mặt khác: $\sum b^2c^2 \geq abc(a+b+c)$ nên chỉ cần chứng minh $a+b+c\geq abc(a^2+b^2+c^2)$

$<=>(a+b+c)+2(ab+bc+ca)abc\geq 9abc$

Sử dụng AM-GM 3 số ta được:

$(a+b+c)+2(ab+bc+ca)abc\geq 3.\sqrt[3]{(a+b+c)(ab+bc+ca)^2a^2b^2c^2}\geq 3.\sqrt[3]{27a^3b^3c^3}=9abc$

Vậy BĐT được chứng minh hoàn toàn

4.Chuẩn hóa rồi dùng UCT là OK

Tạp chí Epsilon số 7. Nguồn: https://www.facebook...hoche.7?fref=ts  (GS Ngô Bảo Châu).

Một bài tương tự:

Tìm tất cả các số thực $k$ để bất đẳng thức sau đúng với mọi số thực không âm $a,b,c$:

\[k\left(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\right)\leqslant \dfrac{a^2+b^2+c^2}{ab+bc+ca}+\dfrac{3k-2}{2}\]

(Những viên kim cương trong bất đẳng thức toán học, trang 604)

Không biết hai bất đẳng thức này có tương đương không mà điểm rơi giống nhau và thằng $k$ cũng chả khác nhau mấy.

BĐT này tương đương với:

$2(a^2+b^2+c^2-ab-bc-ca)\geq\frac{k(a-b)(a-c)(b-c)(ab+bc+ca)}{(a+b)(b+c)(c+a)}$ nên nó gần như giống với đề tháng 12 này, chỉ khác ở chỗ một bên là $k$ với dấu giá trị tuyệt đối, một bên là $\frac{k}{2}$.

Gọi $D$ là giao của $AK$ và $EF$, $N$ là giao của $AM$ với $(O)$, $Q$ là giao điểm của $PF$ với $AB$ và $T$ là giao điểm của $PE$ với $AC$.

Trước tiên, ta sẽ chứng minh $D$ là giao của $AM$ và $EF$.

Giả sử $D'$ là giao của $AM$ và $EF$ vậy thì ta sẽ chứng minh $AD'\perp EF$:

Thật vậy: $TQ$ là đường trung bình của tam giác $PEF$ nên $TQ//EF$.

Nhận thấy tứ giác $AQPT$ nội tiếp (vì có $\widehat{AQP}=\widehat{ATP}=90^{\circ}$)

Nên $\widehat{APQ}=\widehat{ATQ}$

Kết hợp với $AP$ là đường đối trung của tam giác ABC dẫn đến:

$\widehat{MAT}+\widehat{ATQ}=\widehat{QAP}+\widehat{APQ}=90^{\circ}$

Do đó: $AD'\perp EF$ nên $D'\equiv D$

Ta có: $\Delta BNC=\Delta CPB(g-c-g)$ nên dẫn đến $BCNP$ là hình thang cân suy ra $OM$ là đường trung trực của $NP$ nên $MN=MP$

Nếu lấy điểm $D''$ thuộc tia $MA$ thỏa mãn $MD''=MN$ thì $D''$ sẽ đối xứng với $P$ qua $BC$.

Theo tính chất đường thẳng Steiner thì $F,D'',E$ thẳng hàng, mà $D''$ là giao của $EF$ với $AM$ nên $D''\equiv D$

$=>PD\perp AL$     (1)

Lại xét tam giác vuông $LAK$ có $DA=DK$ nên $DA=DL$ dẫn đến $D$ thuộc đường trung trực của $AL$  (2)

Từ (1) và (2) suy ra $PD$ chính là đường trung trực của $AL$.

Vậy $PA=PL$

Giống cách của em http://diendantoanho...án-chuyên-khtn/

Thực ra bài này có thể tổng quát lên thành tìm min của $\sum (\frac{kx-y}{x-y})^2$ với số thực $k$ bất kì nhé  

Cho $x,y,z$ là những số thực dương. Tìm giá trị nhỏ nhất của biểu thức:

$P=\left ( \frac{2x-y}{x-y} \right )^{2}+\left ( \frac{2y-z}{y-z} \right )^{2}+\left ( \frac{2z-x}{z-x} \right )^{2}$

Đặt: $\frac{2x-y}{x-y}=a;\frac{2y-z}{y-z}=b;\frac{2z-x}{z-x}=c$

Ta có:$\frac{x+y}{x-y}=2a-3;\frac{y+z}{y-z}=2b-3;\frac{z+x}{z-x}=2c-3$

Do đó $\sum(2a-3)(2b-3)=-1$

$<=>4(ab+bc+ca)-12(a+b+c)+27=-1<=>(a+b+c)^2-6(a+b+c)^2+14=(a^2+b^2+c^2)$

Suy ra $a^2+b^2+c^2=(a+b+c-3)^2+5\geq 5$

Dấu bằng xảy ra $<=>a+b+c=3<=>\frac{x}{x-y}+\frac{y}{y-z}+\frac{z}{z-x}=0$

(Ngang đây chắc sẽ tìm ra bộ số (x,y,z) nào đó thỏa mãn, việc này nhường cho bạn )

Spoiler

Happy lunar new year

Bài toán: Cho $x,y,z$ là các số không âm, chứng minh:

$$xyz+x^2+y^2+z^2+5\geq 3(x+y+z)$$

Sử dụng bí thuật "Đi-dép-lê" giả sử $(x-1)(y-1)\geq 0$

Khi đó: $xy\geq x+y-1$

Do đó: $xyz+x^2+y^2+z^2+5\geq z(x+y-1)+x^2+y^2+z^2+5=\frac{(x+z)^2}{2}+\frac{(y+z)^2}{2}+\frac{x^2}{2}+\frac{y^2}{2}-z+5\geq 3x+3y+3z$

Ngang đây chú ý AM-GM là OK

Cho ba số x,y,z dương. Chứng minh rằng: 

 

$\frac{(x+1)(y+1)^{2})}{3\sqrt[3]{z^{2}x^{2}}+1} + \frac{(y+1)(z+1)^{2}}{3\sqrt[3]{x^{2}y^{2}}+1} + \frac{(z+1)(x+1)^{2}}{3\sqrt[3]{y^{2}z^{2}}+1} \geq x + y + z + 3$

Để ý: $3\sqrt[3]{x^2z^2}+1\leq xz+x+z+1=(x+1)(z+1)$

Tương tự với 2 cái kia rồi thay vào sử dụng BĐT C-S là OK

 Câu iii) UCT cho lẹ

 

 Ta có : BĐT$\Leftrightarrow \sum \left (\dfrac{a}{27}-\dfrac{a}{3a^2+abc+27}\right )\geq \dfrac{12}{31}$

                    $\Leftrightarrow \sum \dfrac{3a^3+a^2bc}{3a^2+abc+27}\geq \dfrac{12}{31}$

 Áp dụng BĐT Cauchy-Schwarz ta có :

$$\sum \dfrac{3a^3}{3a^2+a^2bc+27}\geq \dfrac{3(a^2+b^2+c^2)^2}{3(a^3+b^3+c^3)+3abc+81}$$

$$abc\sum \dfrac{a}{3a^2+abc+27}\geq \dfrac{9abc}{3(a^3+b^3+c^3)+3abc+81}$$

 Nên ta chỉ cần chứng minh $\dfrac{3(a^2+b^2+c^2)^2+9abc}{3(a^3+b^3+c^3)+3abc+81}\geq \dfrac{12}{31}$

Hay $93(a^2+b^2+c^2)^2+279abc\geq 36(a^3+b^3+c^3)+36abc+972$

       $\Leftrightarrow 93(a^2+b^2+c^2)^2+243abc\geq 36(a^3+b^3+c^3)+972$

 Đặt $p=a+b+c=3;q=ab+bc+ca;r=abc$ thì ta cần chứng minh

       $93(9-2q)^2+243r\geq 36(27-9q+3r)+972$

       $\Leftrightarrow 124q^2-1008q+1863+45r\geq 0$

 Áp dụng BĐT Schur ta có $r\geq \dfrac{4q-9}{3}$ nên ta chỉ cần chứng minh

       $124q^2-1008q+1863+15(4q-9)\geq 0\Leftrightarrow (q-3)(31q-144)\geq 0$

 Luôn đúng vì $q\leq 3$

 Vậy BĐT được chứng minh xong. Dấu "=" xảy ra khi $a=b=c=1$

iii) UCT không được, tính đạo hàm cấp 2 ra $\leq 0$ nhé!

$i)$ Cho các số dương $a;b;c$ thỏa mãn $a^{2}+b^{2}+c^{2} \geq 3$
Chứng minh rằng $(a^{2}+b^{2}+abc)(b^{2}+c^{2}+abc)(c^{2}+a^{2}+abc) \geq 3abc(a+b+c)^{2}$
$ii)$ Cho $a;b;c>0$ và $a+b+c=3$. Chứng minh rằng

$\frac{a}{3a^{2}+abc+27}+\frac{b}{3b^{2}+abc+27}+\frac{c}{3c^{2}+abc+27} \leq \frac{3}{31}$

$iii)$ Cho các số dương $a;b;c$ thỏa mãn $a+b+c=3$
Chứng minh rằng $\sqrt{\frac{a+b}{c+ab}}+\sqrt{\frac{b+c}{a+bc}}+\sqrt{\frac{c+a}{b+ca}} \geq 3$

Câu $iii)$

Áp dụng BĐT AM-GM thì cần chứng minh: $(a+b)(b+c)(c+a)\geq (c+ab)(a+bc)(b+ca)$

Ta có: $(c+ab)(a+bc)\leq \frac{[c+a+b(c+a)]^2}{4}=\frac{(c+a)^2(b+1)^2}{4}$

Tương tự 2 BĐT kia rồi nhân lại AM-GM phát nữa là ra.

P/s: Thầy có ra bài iii) đâu nhỉ

Câu $ii)$ còn một khoảng "rất nhỏ" giữa $1$ với $1,05$ mà không ra, ức chế thật