Cho tớ hỏi diễn đàn mình có hỗ trợ gói lệnh vẽ hình PSTricks gì đó hôm?
LzuTao nội dung
Có 341 mục bởi LzuTao (Tìm giới hạn từ 24-05-2020)
#572875 [Topic]Hỏi đáp về việc Vẽ Hình!
 Đã gửi bởi
LzuTao
on 15-07-2015 - 21:51
trong
Vẽ hình trên diễn đàn
Đã gửi bởi
LzuTao
on 15-07-2015 - 21:51
trong
Vẽ hình trên diễn đàn
#572760 $(x^{2}-\frac{1}{x})^{20}+(...
 Đã gửi bởi
LzuTao
on 15-07-2015 - 16:35
trong
Tổ hợp - Xác suất và thống kê - Số phức
Đã gửi bởi
LzuTao
on 15-07-2015 - 16:35
trong
Tổ hợp - Xác suất và thống kê - Số phức
$A=(x^{2}-\frac{1}{x})^{20}$
$B=(x^{3}-\frac{1}{x})^{10}$
Theo nhị thức Newton:
$A=C_{20}^{k}x^{40-3k}(-1)^k\Rightarrow A$ có 21 số hạng
$B=C_{10}^{l}x^{30-4l}(-1)^l\Rightarrow B$ có 11 số hạng
Để rút gọn, ta phải tìm số số hạng của A & B trùng nhau, tức là tìm $k$ & $l$ sao cho $40-3k=30-4l$ hay $3k-4l=10$, cho $l$ chạy từ $0\rightarrow 10$ ta tìm được 3 số $l$: $2, 5, 8$
Vậy $A+B$ có $21+11-3=29$ số hạng.
#584245 $(1+a+a^2)(1+b+b^2)(1+c+c^2) \leq (1+a+b^2)(1+b+c^2)(1+c+a^2).$
 Đã gửi bởi
LzuTao
on 23-08-2015 - 09:48
trong
Bất đẳng thức và cực trị
Đã gửi bởi
LzuTao
on 23-08-2015 - 09:48
trong
Bất đẳng thức và cực trị
Cho $a, b, c >0$. CMR: $$(1+a+a^2)(1+b+b^2)(1+c+c^2) \leq (1+a+b^2)(1+b+c^2)(1+c+a^2).$$
#580520 $(1+\frac{sinB}{sinA})(1+\frac{sinA...
 Đã gửi bởi
LzuTao
on 11-08-2015 - 00:56
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 11-08-2015 - 00:56
trong
Công thức lượng giác, hàm số lượng giác
Cho tam giác ABC không nhọn có các góc thỏa mãn đẳng thức :
$(1+\frac{sinB}{sinA})(1+\frac{sinA}{sinC})(1+\frac{sinC}{sinB})=4+3\sqrt{2}$
Hỏi tam giác ABC là tam giác gì?
Áp dụng ĐL $\sin$ ta có: $\displaystyle {(1+\frac{\sin B}{\sin A})(1+\frac{\sin A}{\sin C})(1+\frac{\sin C}{\sin B})=4+3\sqrt{2}\\\iff \left ( 1+\frac ba \right )\left ( 1+\frac ac \right )\left ( 1+\frac cb \right )=4+3\sqrt2\\\iff \frac a b +\frac a c +\frac b a +\frac c a+\left (\frac b c +\frac c b \right ) = 2+3\sqrt2\\\iff \left ( b+c \right )\left ( \frac{a}{bc}+\frac{1}a \right )+\left (\frac b c +\frac c b \right ) =2+3\sqrt2\quad \color{red}{(1)}}$
Giờ ta cần chứng minh $VT \ge VP$
Không mất tính tổng quát, cho $a$ là cạnh lớn nhất. Do $\triangle ABC$ không nhọn $\implies a^2\ge b^2+c^2\ge 2bc$
Ta có: $b+c\ge 2\sqrt{bc},\quad \frac{a}{2bc}+\frac{a}{2bc}+\frac{1}a\ge3\sqrt[3]{\frac{a}{4b^2c^2}}\ge 3\sqrt[3]{\frac{\sqrt{2bc}}{4b^2c^2}}=\frac{3}{\sqrt{2bc}}\\\implies \left ( b+c \right )\left ( \frac{a}{bc}+\frac{1}a \right )\ge 3\sqrt2,\quad \left (\frac b c +\frac c b \right ) \ge 2$
Do đó $VT\ge VP$
Đẳng thức xảy ra $\iff a^2=b^2+c^2$ và $b=c$ hay $\triangle ABC$ vuông cân. $\blacksquare$
#586259 $(\frac{sinx}{x})^3\geq cos^{2}x...
 Đã gửi bởi
LzuTao
on 30-08-2015 - 21:23
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 30-08-2015 - 21:23
trong
Công thức lượng giác, hàm số lượng giác
Chứng minh bất đẳng thức:
$(\frac{\sin x}{x})^3\geq \cos^{2}x$ với mọi $x\epsilon (0;\frac{\pi }{2})$
Ta có 2 cách chứng minh:
$\bullet$ Cách 1:
Vì $x\in \left ( 0;\frac\pi2 \right )$ nên ta có : $\tan x>0, \sin x>0, \cos x>0$, biến đổi ta được bất đẳng thức tương đương:
$$\tan^2x\sin x\ge x^3\tag{1}$$
Xét $f(x)=\tan^2x\sin x - x^3$
#586302 $(\frac{sinx}{x})^3\geq cos^{2}x...
 Đã gửi bởi
LzuTao
on 30-08-2015 - 23:34
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 30-08-2015 - 23:34
trong
Công thức lượng giác, hàm số lượng giác
$\bullet$ Cách 2:
Mò mãi mới ra ![]()
Ta cm bổ đề sau: $$\forall x\in \left(0,\frac\pi2\right), \frac{\sin x}x>1-\frac{x^2}6\tag{1}$$ hay $\sin x>x-\frac{x^3}6$
Đặt $f(x)=\sin x-x+\frac{x^3}6$
Ta có:
Từ đó có ĐPCM.
___________________________________________________________________
Ta có thể biến đổi BĐT ban đầu về dạng: $$f(x)= \sin^3(x)-x^3\cos^2(x)$$
Ta có: \begin{align*} f'(x)&= -3x^2\cos^2(x)+2x^3\sin(x)\cos (x)+3\sin^2(x)\cos (x)\\\iff \frac{f'(x)}{x^2\cos x}&=-3\cos x+2x\sin x+3\cdot \left ( \frac{\sin x}{x} \right )^2\\&>-3\cos x+2x^2\left ( 1-\frac{x^2}6 \right )+3\cdot \left ( 1-\frac{x^2}6 \right )^2\\&=x^2+3\left ( 1-\cos x \right )>0\end{align*}
Từ đó suy ra $f'(x)>0$ hay $f(x)\ge f(0)=0$
Q.E.D
![]()
#580600 $\boxed{TOPIC}$ Post Ảnh Hồi Bé (Hồi BaBy)
 Đã gửi bởi
LzuTao
on 11-08-2015 - 12:08
trong
Góc giao lưu
Đã gửi bởi
LzuTao
on 11-08-2015 - 12:08
trong
Góc giao lưu
Được sự uỷ thác của ..... bản thân, Votruc và nhận thấy rằng những ký ức hồi bé là một trong những kỷ niệm đáng nhớ nhất trong đời người, mình xin lập TOPIC Post Ảnh Hồi Bé cho vui. Xin các bạn bình luận một cách vui vẻ, thân thiện. Khi post ảnh có thể nêu rõ được kỷ niệm khi chụp bức ảnh là gì thì càng tốt. ![]()
Đầu tiên là ảnh của mình.
Hơi ngố phải hông? Kỷ niệm năm 2 tuổi hay nhỏ hơn hay sao ý. Lần đầu tiên được chụp ảnh nên có vẻ hơi bất ngờ ![]()
#581112 $\boxed{TOPIC}$ Post Ảnh Hồi Bé (Hồi BaBy)
 Đã gửi bởi
LzuTao
on 12-08-2015 - 22:12
trong
Góc giao lưu
Đã gửi bởi
LzuTao
on 12-08-2015 - 22:12
trong
Góc giao lưu
sao nhìn anh mặt cứ đơ đơ thế nhỉ
![]() Này, không khen anh một tiếng 'hồi nhỏ trông anh đẹp trai thế' thì thôi, sao lại nói những câu làm tim anh tan nát vậy
Này, không khen anh một tiếng 'hồi nhỏ trông anh đẹp trai thế' thì thôi, sao lại nói những câu làm tim anh tan nát vậy ![]() Để kiếm ảnh lớn hơn và đẹp trai hơn post lên.
Để kiếm ảnh lớn hơn và đẹp trai hơn post lên. ![]()
#580612 $\boxed{TOPIC}$ Post Ảnh Hồi Bé (Hồi BaBy)
 Đã gửi bởi
LzuTao
on 11-08-2015 - 13:40
trong
Góc giao lưu
Đã gửi bởi
LzuTao
on 11-08-2015 - 13:40
trong
Góc giao lưu
TẠI ẢNH LÂU RỒI NÊN HƠI MỜ. hÒI XƯA NHÌN ĐÁNG YÊU QUÁ


Anh thấy hồi nhỏ nhìn em ngầu ghê ![]()
#580685 $\boxed{TOPIC}$ Post Ảnh Hồi Bé (Hồi BaBy)
 Đã gửi bởi
LzuTao
on 11-08-2015 - 18:51
trong
Góc giao lưu
Đã gửi bởi
LzuTao
on 11-08-2015 - 18:51
trong
Góc giao lưu
Ảnh năm mình lớp 2,thi đấu cờ vua lần đầu tiên
![]() Có phải em là cậu bé 'tự tin nhất' trong ảnh không?
Có phải em là cậu bé 'tự tin nhất' trong ảnh không? ![]()
![]()
#575082 $$a)\sum_{k=1}^{n}{\frac{1...
 Đã gửi bởi
LzuTao
on 24-07-2015 - 19:09
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 24-07-2015 - 19:09
trong
Công thức lượng giác, hàm số lượng giác
Câu a) tớ đã làm tại đây
#579782 $$(cos\alpha - 1)x^2+2x.sin\alpha -3+sin\alpha <...
 Đã gửi bởi
LzuTao
on 08-08-2015 - 18:46
trong
Phương trình, Hệ phương trình Lượng giác
Đã gửi bởi
LzuTao
on 08-08-2015 - 18:46
trong
Phương trình, Hệ phương trình Lượng giác
$$Cho 0\leq \alpha \leq \frac{\pi }{2}. Chứng minh rằng bất phương trình : (cos\alpha - 1)x^2+2x.sin\alpha -3+sin\alpha < 0$$ nghiệm đúng với mọi x là số thực
Sau khi xét trường hợp $$cos\alpha = 1$$, trường hợp 2, đến xét biệt số delta', em chưa làm được delta' < 0 ạ. Xin các bạn/anh chị giúp em hướng ạ:-?
Đặt $t=\tan\frac{a}{2}\ge 0\Rightarrow \sin a=\frac{2t}{1+t^2}, \ \ \cos a=\frac{1-t^2}{1+t^2}$
Thế vào bất phương trình và thu gọn, ta được:
$$f\left ( t \right )=-2t^2x^2+4tx-3t^2+2t-3<0\\\Delta'_{f(t)}=t^2\left ( -2t^2+4t-3 \right )\le0, \ \ \forall t\ge0$$
Từ đó suy ra đpcm.$\blacksquare$
![]()
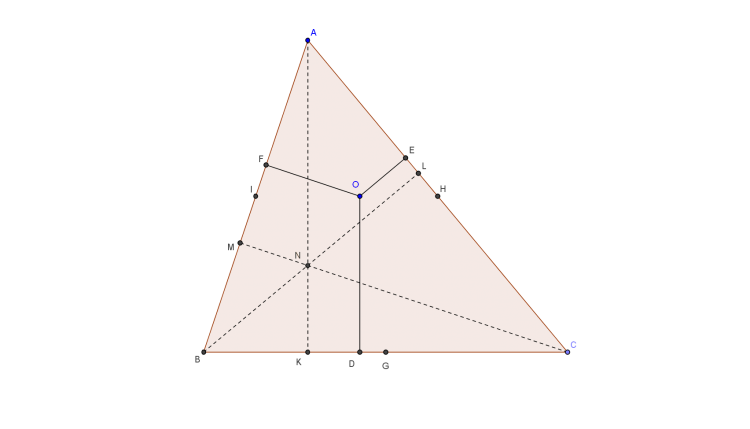
#578024 $$\cot{ADB} + \cot{BEC} + \cot...
 Đã gửi bởi
LzuTao
on 02-08-2015 - 23:14
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 02-08-2015 - 23:14
trong
Công thức lượng giác, hàm số lượng giác
Theo Carnot (Tự lên Google nhé): $$\left(BD^2 - CD^2\right) + \left(CE^2 - AE^2\right) + \left(AF^2 - BF^2\right) = 0\qquad {\color{Red} {(1)}}$$
Đặt $G, H, I$ theo thứ tự là trung điểm $BC, CA, AB$
Ta có: $\overline{BG}=-\overline{CG}\Rightarrow \overline{BG}+\overline{CG}=0\\\left\{\begin{matrix} \overline{BD}=\overline{BG}+\overline{GD} \\\overline{CD}=\overline{CG}+\overline{GD} \end{matrix}\right.\\\Rightarrow \overline{BD}+\overline{CD}=2\overline{GD}\\\Rightarrow BD^2 - CD^2=\left ( \overline{BD}-\overline{CD} \right )\left ( \overline{BD}+\overline{CD} \right )=2\cdot\overline{GD}\cdot \overline{BC}$
Tương tự: $CE^2 - AE^2=2\cdot\overline{HE}\cdot \overline{CA}$ và $AF^2 - BF^2=2\cdot\overline{IF}\cdot \overline{AB}$
Thay vào ${\color{Red} {(1)}}$ ta được:
$$\overline{GD}\cdot \overline{BC}+\overline{HE}\cdot \overline{CA}+\overline{IF}\cdot \overline{AB}=0 \qquad{\color{Red} {(2)}}$$
Gọi $N$ là trực tâm $\triangle ABC$, $K, L, M$ theo thứ tự là chân đường cao kẻ từ $N$ đến $BC, CA, AB$.
Thay $N, K, L, M$ lần lượt vào $O, D, E, F$ ta được:
$\overline{GK}\cdot \overline{BC}+\overline{HL}\cdot \overline{CA}+\overline{IM}\cdot \overline{AB}=0$
Trừ cho ${\color{Red} {(2)}}$ ta được: $$\overline{DK}\cdot \overline{BC}+\overline{EL}\cdot \overline{CA}+\overline{FM}\cdot \overline{AB}=0 \qquad{\color{Red} {(3)}}$$
Gọi $\Delta$ là diện tích $\triangle ABC$, ta có:
$\Delta=\dfrac{1}{2}\cdot \overline{AK}\cdot \overline{BC}=\dfrac{1}{2}\cdot \overline{BL}\cdot \overline{CA}=\dfrac{1}{2}\cdot \overline{CM}\cdot \overline{AB}$
Rút $\overline{BC}, \overline{CA}, \overline{AB}$ và thay vào ${\color{Red} {(3)}}$ ta được:
$\dfrac{\overline{DK}}{\overline{AK}}+\dfrac{\overline{EL}}{\overline{BL}}+\dfrac{\overline{FM}}{\overline{CM}}=0\Rightarrow \frac{DK}{AK}+\frac{EL}{BL}-\frac{FM}{CM}=0\\\Leftrightarrow \cot{ADB} + \cot{BEC} + \cot{CFA} =0$
Vậy bài toán đã được chứng minh.
#582752 $ S=z+z^2+z^3+..................+z^n+\dfrac{1}{z...
 Đã gửi bởi
LzuTao
on 18-08-2015 - 07:57
trong
Tổ hợp - Xác suất và thống kê - Số phức
Đã gửi bởi
LzuTao
on 18-08-2015 - 07:57
trong
Tổ hợp - Xác suất và thống kê - Số phức
Cho số phức $ z $ thỏa mãn $ z + \dfrac{1}{z}=1 $
Hãy tính giá trị $ S=z+z^2+z^3+..................+z^n+\dfrac{1}{z}+\dfrac{1}{z^2}+\dfrac{1}{z^3}+............+\dfrac{1}{z^n} $
Đặt $z=r\left(\cos\varphi+i\sin\varphi\right)\implies z+\frac 1z=\frac{(r^3+1)\cos x+(r^3-1)\sin x}{r^2}=1\iff r^3-1=0\iff r=1$
Vì $\cos $ đối và có chu kỳ $2\pi$ nên ta chọn $\varphi=\frac\pi3$.
Ta có: $z^n+\frac1{z^n}=2\cos \frac{n\pi}{3}$ do đó:
$S=2\left(\cos\frac\pi3+\cdots+\cos\frac{n\pi}{3}\right)\\\iff\frac{\sqrt3}2\cdot S=\sin\frac\pi3\cdot 2\left(\cos\frac\pi3+\cdots+\cos\frac{n\pi}{3}\right) \\\iff \frac{\sqrt3}2\cdot S = \sin\frac{2\pi}3+\sin\frac{3\pi}{3}-\sin\frac{\pi}{3}+\sin\frac{4\pi}{3}-\sin\frac{2\pi}3+\cdots+\sin\frac{(n+1)\pi}{3}-\sin\frac{(n-1)\pi}{3}\\ \iff \frac{\sqrt3}2\cdot S = -\sin\frac{\pi}{3}+ \sin\frac{n\pi}{3}+\sin\frac{(n+1)\pi}{3}\\ \iff \frac{\sqrt3}2\cdot S = -\frac{\sqrt3}2+\sqrt3\sin\frac{(2n+1)\pi}{6}\\ \iff S=-1+2 \sin\frac{(2n+1)\pi}{6}$
Vẽ đường tròn lượng giác, ta có:
- $n=6k, (k\in \mathbb{N}, n\neq 0)\implies S=-1+2\sin\frac{(12k+1)\pi}{6}=-1+2\sin\frac{\pi}{6}=0$
- $n=6k+1\implies S=-1+2 \sin\frac{(12k+3)\pi}{6}=1$
- $n=6k+2\implies S=-1+2\sin\frac{(12k+5)\pi}{6}=0$
- $n=6k+3\implies S=-1+2\sin\frac{(12k+7)\pi}6=-2$
- $n=6k+4\implies S=-1+2\sin\frac{(12k+9)\pi}6=-3$
- $n=6k+5\implies S=-1+2\sin\frac{(12k+11)\pi}6=-2.\blacksquare$
#575382 $ cot C=2(cotA + cotB)$
 Đã gửi bởi
LzuTao
on 25-07-2015 - 21:06
trong
Công thức lượng giác, hàm số lượng giác
Đã gửi bởi
LzuTao
on 25-07-2015 - 21:06
trong
Công thức lượng giác, hàm số lượng giác
1.CM các công thức sau
a) $cos\frac{\pi }{7}-cos\frac{2\pi }{7}+cos\frac{3\pi }{7}=\frac{1}{2}$
b) $cos\frac{\pi }{5}-cos\frac{2\pi }{5}=\frac{1}{2}$
1a) Ta có:
$2\sin\dfrac{\pi }{7}\cos\dfrac{\pi }{7}=\sin\dfrac{2\pi }{7} $
$-2\sin\dfrac{\pi }{7}\cos\dfrac{2\pi }{7}=\sin\dfrac{\pi }{7}-\sin\dfrac{3\pi }{7}$
$2\sin\dfrac{\pi }{7}\cos\dfrac{3\pi }{7}=\sin\dfrac{4\pi }{7}-\sin\dfrac{2\pi }{7}$
Cộng từng vế và rút gọn là được.
1b) Nhân cả hai vế với $2\sin\dfrac{\pi }{5}$ ta được: $\sin\dfrac{2\pi }{5}-\left ( \sin\dfrac{3\pi }{5}-\sin\dfrac{\pi }{5} \right )=\sin\dfrac{\pi }{5}=VP$
- Diễn đàn Toán học
- → LzuTao nội dung