Bài này mình có đưa lên diễn đàn một lần rồi, bạn xem tại đây hoặc trong bài viết "đường tròn phụ trong một số bài toán tiếp xúc"!

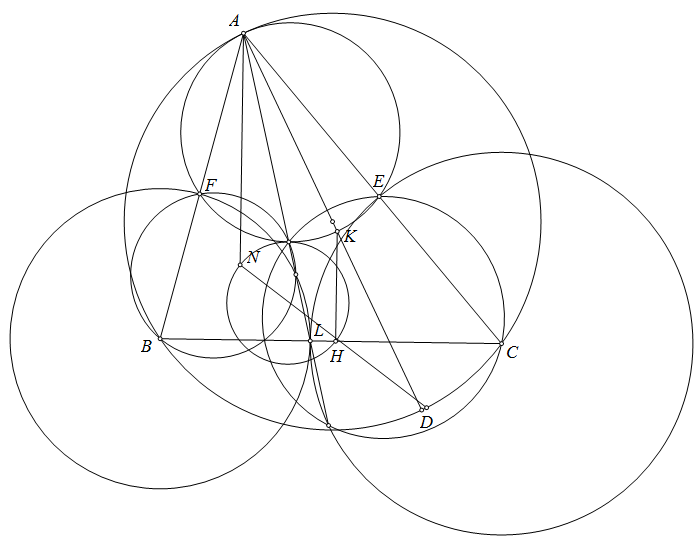
Bài toán. (Thầy Trần Quang Hùng} Cho tam giác $ABC$, đường kính $AD$. Phân giác $AL(L$ thuộc $BC).E,F$ lần lượt thuộc $CA,AB$ sao cho $CE=CL,BE=BL.(AEF)$ cắt $AD$ tại $K$. Kẻ $KH\perp BC.DH$ cắt đường cao ứng với đỉnh $A$ của tam giác $ABC$ tại $N$. Chứng minh rằng $(NH)$ tiếp xúc $(AEF).$ 

Hình vẽ bài toán

P/s

Trên hình mình đã có một số gợi ý liên quan!

Cho dãy số $F_1,F_2,..,F_n$ được xác định như sau : $F_1=1,F_2=-1,..,F_n=-F_{n-1}-2F_{n-2}$ với $n$ là số tự nhiên lớn hơn $3$. Hỏi số $S_n=2^{n+1}-2F_{n-1}^2$ với $n$ là số tự nhiên lớn hơn $3$ có là số chính phương hay không ? 

Mình không biết có hiểu lầm không nhưng theo mình thì bài này dễ và phù hợp với $THCS$!

Ta chứng minh bằng quy nạp $F_{n}$ lẻ với mọi $n$ thuộc $N*$.

$n=1$: mệnh đề đúng

Giả sử mệnh đề đúng với $n=k$ tức là $F_{k}$ lẻ, ta chứng minh nó đúng với $n=k+1$

Do $F_{k}$ lẻ, $2F_{k-1}$ chẵn nên $F_{k+1}$ lẻ. Vậy mệnh đề đúng với $n=k+1$

Theo nguyên lí quy nạp ta suy ra $F_{n}$ lẻ với mọi $n$ thuộc $N*$.

Ta có $S_{n}=2(2^{n}-F_{n-1}^{2})$ chẵn nên $S_{n}$ là số chính phương khi và chỉ khi $S_{n}\vdots 4$. Mặt khác do $F_{n-1}^{2}$ lẻ nên $2^{n}-F_{n-1}^{2}$ lẻ

Vậy $S_{n}$ không thể là số chính phương.

P/s:

Bài này khá hay, mô hình nó khá giống với bài hình học ngày 2 Vietnam TST 2015! Ngoài tính chất trên nó còn có nhiều tính chất khác rất thú vị!

Lời giải của mình: Để giải quyết bài toán, ta cần có bổ đề sau: Cho $\triangle ABC$ cân nội tiếp $(O)$. $D$ là điểm bất kì trên cung $BC$ không chứa $A$. Khi đó: 

$\frac {AD}{AC}=\frac {BD+DC}{BC}$.

Chứng minh: Trên $BD$ lấy $E$ sao cho $DE=DC$. Do $\triangle CDE$ cân tại $D$ nên ta có biến đổi góc: $\angle CED=\angle CDB/2= \angle ADC $. Mặt khác lại có:

$\angle CAD=\angle CBD \Rightarrow \triangle CAD \sim \triangle CBE$

$\Rightarrow \frac {AD}{AC}=\frac {BE}{BC}=\frac {BD+DC}{BC}$. Bổ đề được chứng minh.

Quay lại với bài toán: Nhận xét rằng: $\angle BAP=\angle ACP, \angle CAP=\angle ABP$ nên $(APB)$ tiếp xúc $AC$ và đi qua $B$; $(APC)$ tiếp xúc $AB$ và đi qua $C$. Dễ thấy $\triangle APB \sim \triangle CPA (g.g)$

Do $M,N$ lần lượt là các tâm nội tiếp $\triangle APB$ và $\triangle APC$ nên dễ dàng suy ra $\triangle MPN \sim \triangle APC ;O$ thuộc $AP$ ($O$ là tâm đường tròn ngoại tiếp tam giác $AMN$); $M,N,O,P$ đồng viên.

$\Rightarrow \frac {AP}{AB}= \frac {PC}{AC} \Rightarrow \frac {1}{R}=\frac {1}{AP}+\frac {1}{AB}+\frac {1}{AC} \Leftrightarrow \frac {AP}{R}=1+\frac {AP}{AB}+\frac {AP}{AC}=1+\frac {PA+PC}{AC}=\frac {MP+PM}{MN}+1 \Leftrightarrow \frac {OP}{R}=\frac {MP+PM}{MN}$

Đẳng thức cuối đúng theo bổ đề nên ta có điều phải chứng minh!

$\textbf{Bài toán.}$ $\textit{(Lim Jeck)}$ $X,Y,Z$ là các điểm nằm trong tam giác $ABC$ sao cho

$\angle BAY=\angle CAZ,\angle CBZ=\angle ABX,\angle ACX=\angle BCY$

Kéo dài $AY,AZ$ cắt $BC$ lần lượt tại $Y_a,Z_a$. Tương tự xác định các điểm $X_b,Z_b,X_c,Y_c$. Giả sử $X_bY_a,Y_cZ_b,Z_aX_c$ đồng quy.

Chứng minh rằng tồn tại các điểm $D,E,F$ lần lượt thuộc các cạnh $BC,CA,AB$ sao cho $X$ thuộc $EF,Y$ thuộc $FD,Z$ thuộc $DE$ và $AD,BE,CF$ đồng quy.

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 3 tháng 11 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán mới,

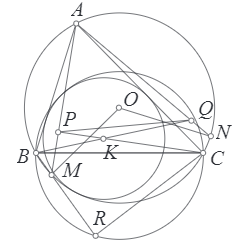
Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn $(K)$ tiếp xúc $CA$, $AB$ và tiếp xúc trong $(O)$.

Gọi $M,N$ lần lượt là trung điểm các cung $CA$, $AB$ chứa $B$, $C$ của $(O)$. $AM$, $AN$ lần lượt cắt $KC$, $KB$ tại $P$, $Q$.

$R$ đối xứng $A$ qua $PQ$. Chứng minh rằng đường tròn ngoại tiếp tam giác $RBC$ tiếp xúc $(K)$.

Hình vẽ bài toán

Một số đặc điểm của đường đối trung được tổng hợp bởi $LuisGonzáles$.

 Đặc trưng của đường đối trung.pdf   131.43K   974 Số lần tải

Cho $f:\mathbb{R}\rightarrow \mathbb{R}$ thỏa mãn: $f(x^n+y^n)=(x+y)(f^{n-1}(x)-f^{n-2}(x)f(y)+...+f^{n-1}(y))\forall x,y\in \mathbb{R},n$ lẻ, $n>1$

Chứng minh rằng $f(ax)=af(x)\forall x\in \mathbb{R}$ và $\forall a\in \mathbb{N}$.

Tiếp tục nào!

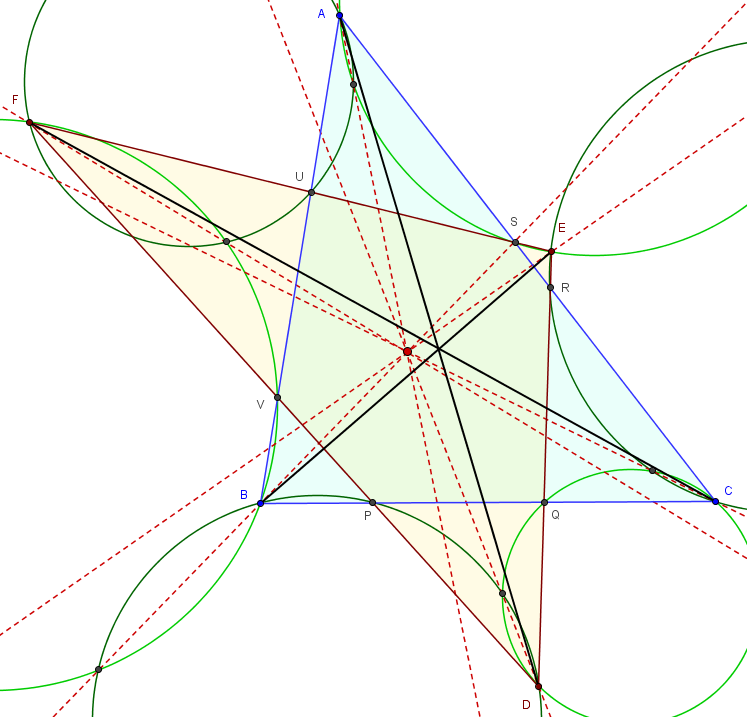
Bài toán. (Tev Cohl) Cho hai tam giác $ABC$ và $DEF$ sao cho $AD,BE,CF$ đồng quy. $P,Q,R,S,U,V$ lần lượt là giao của $BC$ với $FD,BC$ với $DE,CA$ với $DE,CA$ với $EF,AB$ với $EF,AB$ với $FD$. Chứng minh rằng $\odot (BDP),\odot (CDQ),\odot (CER),\odot (AES),\odot (AFU),\odot (BFV)$ có chung tâm đẳng phương.

Hình vẽ bài toán

Một bài rất đẹp nhưng chưa có lời giải!

Cho $ABCD$ là tứ giác nội tiếp. Giả sử $AD$ cắt $BC$ tại $S$. Lấy $I$ thuộc phân giác $\angle DSC$. $AI, BI$ cắt $(O)$ tại $K,L$. Lấy $P$ đối xứng với $C$ qua $OL$. Tương tự lấy điểm $Q$. $R,S$ lần lượt là điểm chính giữa cung nhỏ $DP, QC$. $M,N$ lần lượt là giao của $TP$ với $AR$; $TQ$ với $BS$. ($T$ là điểm chính giữa cung nhỏ $AB$). Chứng minh: $TM=TN$.

Bài toán. (Đào Thanh Oai)  Cho ngũ giác $A_1A_2A_3A_4A_5$ nội tiếp đường tròn $(O)$. Đặt $B_i=A_{i-1}A_i\cap A_{i+1}A_{i+2}$ với mọi $i\in \overline{1,5}$.

$(O_i)$ là đường tròn qua $B_i,A_{i+2},A_{i+4}.C_i$ là giao điểm thứ hai của $O_{i+1}$ và $(O_{i+4}$.

Khi đó $C_1,C_2,C_3,C_4,C_5$ cũng thuộc một đường tròn.

Bổ sung. (baopbc) a) $A_iC_{i+2}$ đồng quy tại $I$.

b) Gọi $J$ là tâm $(C_1C_2C_3C_4C_5)$. Chứng minh $O,I,J$ thẳng hàng.

Spoiler

Bài toán được chú Đào Thanh Oai đưa lên AopS vào chiều nay, không hiểu vì sao lại bị mất , mình xin được đăng lại tại đây!

Hình vẽ