Cho $x,y,z$ là các số dương thỏa mãn  $x+y+z= 1$.

 

Chứng minh:

             

              $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+48(xy+yz+zx)\geq 25$

Đề đã được bạn NHoang1608 đăng tại đây rồi nhé bạn

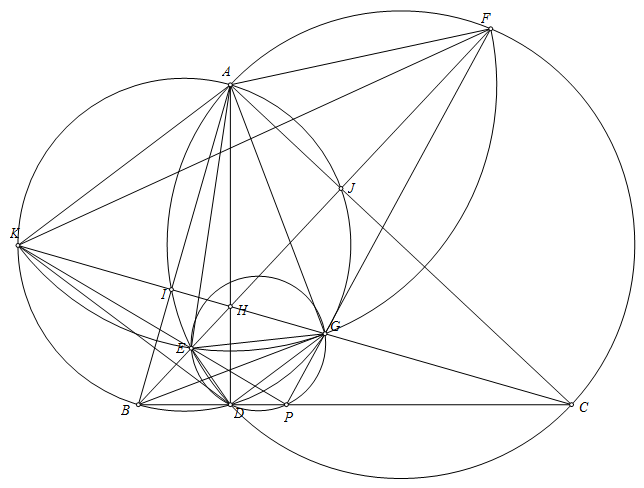
Bài 4.

a) Theo hệ thức lượng: $AE^2=AJ.AC=AI.AB=AG^2 \Rightarrow AE=AG$

A thuộc đường trung trực của $EF$ $\Rightarrow AE=AF$

CMTT: $AG=AK$

$\Rightarrow AE=AG=AK=AF \Rightarrow A$ là tâm đường tròn ngoại tiếp tứ giác $KEGF$

b) $\angle PEG = \angle PDG = \angle BAG = \frac{\angle KAG}{2}$

$\angle KEG = \angle AEK + \angle AEG = 180^{\circ} - \frac{\angle KAG}{2} = 180^{\circ} - \angle PEG \Rightarrow \angle KEG + \angle PEG = 180^{\circ} $

$\Rightarrow P,E,K$ thẳng hàng

c) $\angle KEG + \angle BAK = \angle KEG + \angle KFG=180^{\circ} \Rightarrow \angle KFG = \angle BAK =  \angle BDK$

$\Rightarrow K,D,P,F$ cùng thuộc một đường tròn

Cho $x,y,z$ là các số dương thỏa mãn  $x+y+z= 1$.

 

Chứng minh:

             

              $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+48(xy+yz+zx)\geq 25$

Giả sử $\left ( x-\frac{1}{3}\right )\left ( y - \frac{1}{3} \right ) \ge 0 \Leftrightarrow xy + \frac{1}{9} \ge \frac{1}{3}(x+y)=\frac{1}{3}(1-z) \Rightarrow xy \ge \frac{2}{9} - \frac{1}{3}z$

$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+48(xy+yz+zx)\ge \frac{4}{x+y}+\frac{1}{z}+48\left (\frac{2}{9}- \frac{1}{3}z \right ) + 48z(x+y) = \frac{4}{1-z}+\frac{1}{z}+48\left (\frac{2}{9}- \frac{1}{3}z \right ) + 48z(1-z) \ge 25 $

hình như giải sai lè rồi. cái bổ đề không hợp lý câu b.

Lời giải đã được kiểm chứng thì mình mới dám post lên nhé bạn :/ 

hình như giải sai lè rồi. cái bổ đề không hợp lý câu b.

Có thực sự hợp lý không ? hay là bạn không hiểu ?

Câu Hình có vẻ dễ

Câu 5.

a)

b) Gọi $J$ là giao điểm của $OH$ và $ME$

Dễ thấy $OH \perp MJ$ (1) , $\triangle MHE$ là tam giác vuông cân tại $H$

$\angle COE = \angle CKE = \angle AHE = 90^{\circ} \Rightarrow O,K,C,H,E$ cùng thuộc một đường tròn 

$\Rightarrow \angle KOH + \angle MHO = \angle KEH + \angle MHO = 45^{\circ} + 45^{\circ} = 90^{\circ} \Rightarrow OK \perp MH$ (2)

Từ (1) và (2) suy ra $OM \perp HK$

Câu 4.

a) Bổ đề.  Từ $A$ nằm ngoài đường tròn $(O;R)$ vẽ $2$ tiếp tuyến $AB,AC$ với đường tròn $(O)$ ($B,C$ là các tiếp điểm). Gọi $P,Q$ lần lượt là trung điểm của $AB,AC$. Từ điểm $M$ bất kỳ thuộc cạnh $PQ$ kẻ tiếp tuyến $MD$ của đường tròn. Chứng minh rằng: $MA=MD$

Chứng minh. Gọi $H$ là giao điểm của $OA$ và $BC$

$OD^2=OB^2=OH.OA$ $\Rightarrow$ $OD$ là tiếp tuyến đường tròn $(O)$ 

$\Rightarrow M$ là tâm đường tròn ngoại tiếp tam giác $ADH$ $\Rightarrow MA=MD$

Quay trở lại bài toán. Từ bổ đề ta có được: $KO^2 - KM^2 = R^2$

b) Từ Bổ đề ta có: $KC^2 = KD.KA \Rightarrow \triangle KCD \sim \triangle KAC \Rightarrow \angle KCD = \angle KAC$ hay $ \angle MCD =  \angle BAD =  \angle DBM$ 

$\Rightarrow MDCB$ là tứ giác nội tiếp

c) Gọi $L$ là trung điểm của $KD$

$ \angle AEM =  \angle MAK =  \angle EMK \Rightarrow AE \parallel KM$

$KF.KE = KD.KA \Rightarrow KF.KN=KL.KA \Rightarrow ANKL$ nội tiếp $\Rightarrow \angle LAF = \angle LNF = \angle MEK = \angle FMK$ hay $\angle KAF = \angle KMF$ 

$\Rightarrow MKFA$ nội tiếp $\Rightarrow \angle AFN = \angle AMK = \angle AIN$ $\Rightarrow I,A,N,F$ cùng thuộc một đường tròn

Câu 4.

a) Bổ đề.  Từ $A$ nằm ngoài đường tròn $(O;R)$ vẽ $2$ tiếp tuyến $AB,AC$ với đường tròn $(O)$ ($B,C$ là các tiếp điểm). Gọi $P,Q$ lần lượt là trung điểm của $AB,AC$. Từ điểm $M$ bất kỳ thuộc cạnh $PQ$ kẻ tiếp tuyến $MD$ của đường tròn. Chứng minh rằng: $MA=MD$

Chứng minh. Gọi $H$ là giao điểm của $OA$ và $BC$

$OD^2=OB^2=OH.OA$ $\Rightarrow$ $OD$ là tiếp tuyến đường tròn $(O)$ 

$\Rightarrow M$ là tâm đường tròn ngoại tiếp tam giác $ADH$ $\Rightarrow MA=MD$

Quay trở lại bài toán. Từ bổ đề ta có được: $KO^2 - KM^2 = R^2$

b) Từ Bổ đề ta có: $KC^2 = KD.KA \Rightarrow \triangle KCD \sim \triangle KAC \Rightarrow \angle KCD = \angle KAC$ hay $ \angle MCD =  \angle BAD =  \angle DBM$ 

$\Rightarrow MDCB$ là tứ giác nội tiếp

c) Gọi $L$ là trung điểm của $KD$

$ \angle AEM =  \angle MAK =  \angle EMK \Rightarrow AE \parallel KM$

$KF.KE = KD.KA \Rightarrow KF.KN=KL.KA \Rightarrow ANKL$ nội tiếp $\Rightarrow \angle LAF = \angle LNF = \angle MEK = \angle FMK$ hay $\angle KAF = \angle KMF$ 

$\Rightarrow MKFA$ nội tiếp $\Rightarrow \angle AFN = \angle AMK = \angle AIN$ $\Rightarrow I,A,N,F$ cùng thuộc một đường tròn

Lời giải bài toán 1.

$VT= {\left( {\frac{a}{{b - c}} + \frac{b}{{c - a}} + \frac{c}{{b - a}}} \right)^2} - 2\left( {\frac{{ab}}{{\left( {b - c} \right)\left( {c - a} \right)}} + \frac{{bc}}{{\left( {c - a} \right)\left( {a - b} \right)}} + \frac{{ca}}{{\left( {a - b} \right)\left( {b - c} \right)}}} \right)$

$ = \left ( \frac{a}{b - c} + \frac{b}{c - a} + \frac{c}{b - a} \right) ^2 + 2 \ge 2$

Lời giải bài toán 4.

\[\textbf{Canada MO 2017}\]

Bài Toán 1. Cho $a,b,c$ là các số thực không âm đôi một khác nhau. Chứng minh rằng

$\dfrac{a^2}{(b-c)^2}+\dfrac{b^2}{(c-a)^2}+\dfrac{c^2}{(b-a)^2}>2.$

Bài Toán 2. Cho hàm $f(n)$ từ tập các số nguyên dương đến chính nó sao cho $f(f(n))$ là số ước dương của $n$. Chứng minh rằng nếu $p$ là số nguyên tố thì $f(p)$ là số nguyên tố.

Bài Toán 3. Cho số nguyên dương $n$. Một tập con khác rỗng $T_n$ của $[n]$ được gọi là cân bằng nếu trung bình cộng các phần tử của $T_n$ bằng trung gian của $T_n$. Chứng minh rằng với mỗi số nguyên dương $n$, số tập con cân bằng của $[n]$ là lẻ.

Bài Toán 4. Cho hình bình hành $ABCD$. Các điểm $P,Q$ nằm trong $ABCD$ sao cho $ABP$ và $BCQ$ là các tam giác đều. Chứng minh rằng giao điểm của đường thẳng đi qua $P$ vuông góc với $PD$ và đường thẳng đi qua $Q$ vuông góc với $DQ$ nằm trên đường cao qua $B$ của $\triangle{ABC}$.

Bài Toán 5. Có $100$ đường tròn bán kính $1$ trong mặt phẳng sao cho các tam giác có $3$ đỉnh là $3$ tâm bất kỳ của các đường tròn này có diện tích không vượt quá $2017$. Chứng minh rằng tồn tại một đường thẳng có điểm chung với ít nhất $3$ đường tròn.

Người dịch: Nguyễn Trung Tuân

\[\textbf{IRAN TST 2017}\]

$\text{Ngày thứ nhất}$

Bài Toán 1. Cho số nguyên $n>1$. Chứng minh rằng tồn tại số nguyên $n-1 \ge m \ge \left \lfloor \frac{n}{2} \right \rfloor$ sao cho phương trình sau có nghiệm nguyên thỏa mãn $a_m>0:$

$\displaystyle\frac{a_{m}}{m+1}+\frac{a_{m+1}}{m+2}+ \cdots + \frac{a_{n-1}}{n}=\frac{1}{\textrm{lcm}\left ( 1,2, \cdots , n \right )}.$

Bài Toán 2. Cho $P$ là một điểm nằm trong tứ giác $ABCD$ sao cho

$\angle BPC=2\angle BAC  , \angle PCA = \angle PAD  , \angle PDA=\angle PAC.$

Chứng minh rằng $\angle PBD= \left | \angle BCA - \angle PCA \right |.$

Bài Toán 3. Tìm tất cả các hàm $f: \mathbb {R}^+ \times \mathbb {R}^+ \to \mathbb {R}^+$ thỏa mãn đồng thời hai điều kiện sau với mỗi ba số thực dương $x,y,z$.

1) $f\left ( f(x,y),z \right )=x^2y^2f(x,z).$

2) $f\left ( x,1+f(x,y) \right ) \ge x^2 + xyf(x,x).$

$\text{Ngày thứ hai}$

Bài Toán 4. Cho $6$ điểm nằm trên mặt phẳng sao cho không có ba điểm nào thẳng hàng. Biết rằng trong $4$ điểm bất kỳ trong các điểm đã cho, tồn tại một điểm có phương tích đối với đường tròn đi qua ba điểm còn lại bằng một hằng số $k$. Chứng minh rằng cả $6$ điểm đã cho cùng nằm trên một đường tròn.

Bài Toán 5. Cho $\left \{ c_i \right \}_{i=0}^{\infty}$ là một dãy các số thực không âm thỏa mãn $c_{2017}>0$. Xét dãy đa thức $P_n(x)$ xác định bởi

$P_{-1}(x)=0 \ , \ P_0(x)=1 \ , \ P_{n+1}(x)=xP_n(x)+c_nP_{n-1}(x),\,\forall n\geq 0.$

Chứng minh rằng không tồn tại số nguyên $n>2017$ và số thực $c$ sao cho $P_{2n}(x)=P_n(x^2+c).$

Bài Toán 6. Cho tam giác $ABC$ với tâm ngoại tiếp $O$ và trực tâm $H$. Điểm $P$ đối xứng với $A$ qua $OH$. Giả sử $P$ không nằm trên nửa mặt phẳng bờ $BC$ chứa $A$. Các điểm $E,F$ lần lượt thuộc $AB,AC$ sao cho $BE=PC  , CF=PB$. Gọi $K$ là giao điểm của $AP,OH$. Chứng minh rằng $\angle EKF = 90 ^{\circ}.$

Người dịch: Nguyễn Trung Tuân

ly.PNG

Bạn khgisongsong chú ý không đăng ảnh (Theo như nội quy của topic đã nêu)

Mình xin đề xuất bài mới !

Bài Toán 7. Giải phương trình: $\sqrt[4]{1-x^2}+\sqrt[4]{1+x}+\sqrt[4]{1-x}=3$

Bài Toán 8. Giải hệ phương trình: $\left\{\begin{matrix} x^3(2+\dfrac{3}{y})=1\\ x(\dfrac{1}{y^3}-2)=3\end{matrix}\right.$

Bài Toán 9. Giải hệ phương trình: $\left\{\begin{matrix}x^5-y^5=5x-5y\\ x^4+y^8=1\end{matrix}\right.$

Bài Toán 4.(Baoriven) Giải hệ phương trình: $\left\{\begin{matrix}x^2+y^2=|x-y| \\ 3^{2+x}+3^{2+y}=30 \end{matrix}\right..$

Lời giải bài toán 4.

$3^{2+x}+3^{2+y}=30 \Leftrightarrow 3^x + 3^y = \dfrac{10}{3}$ 

Xét $x \ge 0;y \ge 0$ ta có: Không tồn tại $3^x + 3^y$ có dạng phân số (Loại) 

Xét $x \le 0;y \le 0$ ta có: $3^x + 3^y \le 2 < \dfrac{10}{3}$ (loại)

$\Rightarrow$ $x,y$ là $2$ số trái dấu

Không mất tính tổng quát giả sử $x \ge 0;y \le 0$. Đặt $x=a \ge 0 ; -y=b \ge 0$ ta có:

$\left\{\begin{matrix}a^2+b^2=a+b \\ 3^{2+a}+3^{2-b}=30 \end{matrix}\right.$

$a^2+b^2=a+b \ge \dfrac{(a+b)^2}{2} \Rightarrow 2 \ge a+b \Rightarrow 2-b \ge a$ 

$ \Rightarrow 30=3^{2+a}+3^{2-b} \ge 3^{2+a}+3^a = 10.3^a$

$ \Rightarrow 1 \ge a$ $(1)$

Và $a^2+b^2=a+b \Rightarrow a(a-1)+b(b-1)=0$

Vì $a(a-1) \le 0 \Rightarrow b(b-1) \ge 0 \Rightarrow b \ge 1$ $(2)$

Từ $(1)$ và $(2)$ $ \Rightarrow 3^{2+a}+3^{2-b} \le 3^3 + 3 = 30$

Dấu bằng xảy ra khi: $a=1;b=1$ Hay $x=1;y=-1$

Vậy $\boxed{(x;y)=\begin{Bmatrix}(1;-1);(-1;1)\end{Bmatrix}}$

Mình có đề nghị: Nếu bạn nào giải bài nào thì chỉ trích đề bài đó, không nên trích hết cả như vậy

\[\textbf{Topic ôn thi vào lớp 10 chuyên về Phương Trình - Hệ Phương Trình}\]

Chú ý: - Topic lập ra để ôn thi vào lớp 10.

            - Hạn chế hỏi bài tập về nhà.

            - Nên gõ đề và lời giải bằng $\LaTeX$. Không đăng ảnh để tránh hiện tưởng die ảnh.

            - Hạn chế đề xuất bài mới khi còn nhiều bài toán chưa được giải.

            - Đánh đúng số thứ tự bài toán

Mình xin bắt đầu với một số Bài Toán sau:

Bài Toán 1. Giải phương trình: $7x^{2}+7x=\sqrt{\frac{4x+9}{28}}$

Bài Toán 2. Giải phương trình: $\sqrt[3]{2x+1}+\sqrt[3]{x}=1$

Bài Toán 3. Giải hệ phương trình: $\left\{\begin{matrix} xy^2-2y+3x^2=0\\ y^2+x^2y+2x=0 \end{matrix}\right.$

Bài Toán 4.(Baoriven) Giải hệ phương trình: $\left\{\begin{matrix}x^2+y^2=|x-y| \\ 3^{2+x}+3^{2+y}=30 \end{matrix}\right..$

Bài 4. 

a) Gọi $J$ là giao điểm của $EH$ và $AI$

$\angle EIC + \angle ACB + \angle IAC = \angle EIC + \angle EIt =  \angle EIC + \angle EHC \Rightarrow \angle ACB + \angle IAC = \angle EHC$ $(1)$

Mà $ \angle ACB +  \angle BAC =  \angle AHC$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow \angle IAC = \angle AHE$ hay $ \angle JAE = \angle AHJ$ $\Rightarrow \triangle AJE \sim \triangle HJA \Rightarrow AJ^2 = JE.JH$

$\triangle JIE \sim \triangle JHI \Rightarrow JI^2 = JE.JH$ $\Rightarrow AJ = JI$

b) Chỉ cần chứng minh được $\angle FIG = \angle EIH$. 

Spoiler

Sẽ full câu b) sau  

Bài toán 195. Tam giác $ABC$ có trực tâm $H$, $K$ là một điểm khác $H$ nằm trong tam giác. $H_1,H_2,H_3$ lần lượt là trực tâm tam giác $AHK, BHK, CHK$. $X,Y,Z$ là theo thứ tự là trung điểm $AH_1; BH_2; CH_3$. Chứng minh $X,Y,Z$ thẳng hàng.

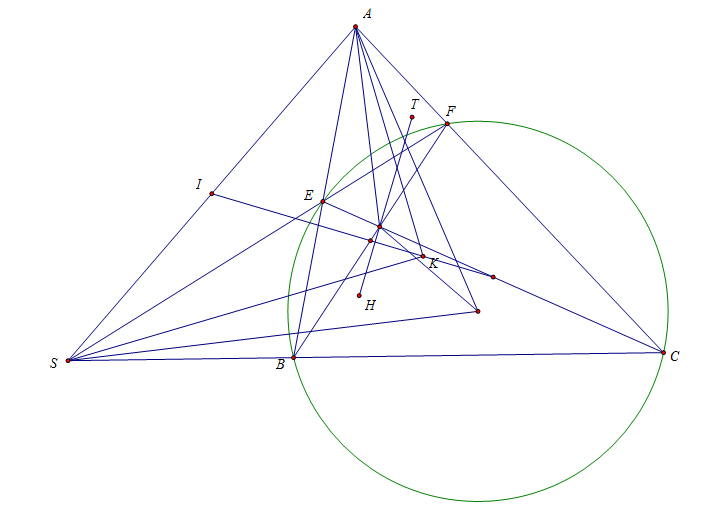
Bài toán 194. Cho tam giác $ABC$ nội tiếp $(O)$. Một đường tròn bất kì qua $B,C$ cắt $AB,AC$ tại $E,F$. $EF$ cắt $BC$ tại $S$. $I$ là trung điểm $AS$. $K$ là hình chiếu của $S$ lên phân giác trong góc $BAC$. Chứng minh rằng đường thẳng qua trực tâm tam giác $ABC$ vuông góc $IK$ đi qua trực tâm tam giác $AEF$.

Bổ đề. Cho tứ giác $ABCD$ nội tiếp được đường tròn. Gọi $E,F$ lần lượt là các giao điểm của $AD$ và $BC$, $AB$ và $CD$. Gọi $I$ là giao điểm của phân giác hai góc $BFC,DEC$. $G,H$ lần lượt là trung điểm của $BD,AC$. Chứng minh rằng $G,H,I$ thẳng hàng.

Chứng minh. Xem tại đây

Quay trở lại bài toán.

Gọi $T$ là trực tâm của tam giác $AEF$.

Từ Bổ đề ta có được: $IK$ là $\text{Gauss}$

Theo tính chất đường thẳng $\text{Gauss}$ vuông góc với đường thẳng $\text{Steiner}$: $IK \perp HT$

Bài này lấy từ đề thi HSG Toán 9 Thừa Thiên Huế 2016-2017

 Cho a, b là các số dương khác nhau thỏa: 

 $a-b=$$\sqrt{1-b^{2}}$-$\sqrt{1-a^{2}}$

Chứng minh : $a^{2} +b^{2} = 1$

\[a-b=\sqrt{1-b^2}-\sqrt{1-a^2} \Leftrightarrow \left (a-\sqrt{1-b^2}  \right )-\left ( b-\sqrt{1-a^2} \right )=0 \Leftrightarrow \frac{a^2+b^2-1}{a+\sqrt{1-b^2}} - \frac{a^2+b^2-1}{b+\sqrt{1-a^2}}=0 \Leftrightarrow \left ( a^2+b^2-1 \right )\left (\frac{1}{a+\sqrt{1-b^2}} - \frac{1}{b+\sqrt{1-a^2}}   \right )=0\]