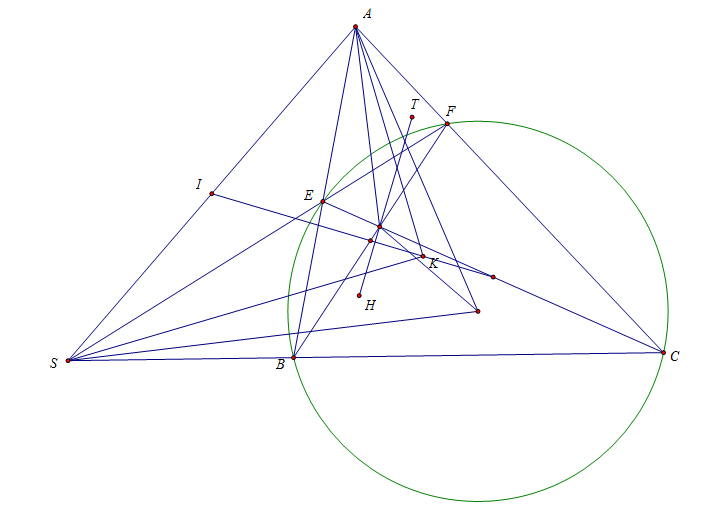
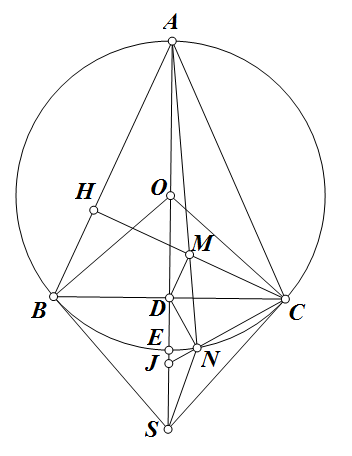
Bài toán 194. Cho tam giác $ABC$ nội tiếp $(O)$. Một đường tròn bất kì qua $B,C$ cắt $AB,AC$ tại $E,F$. $EF$ cắt $BC$ tại $S$. $I$ là trung điểm $AS$. $K$ là hình chiếu của $S$ lên phân giác trong góc $BAC$. Chứng minh rằng đường thẳng qua trực tâm tam giác $ABC$ vuông góc $IK$ đi qua trực tâm tam giác $AEF$.

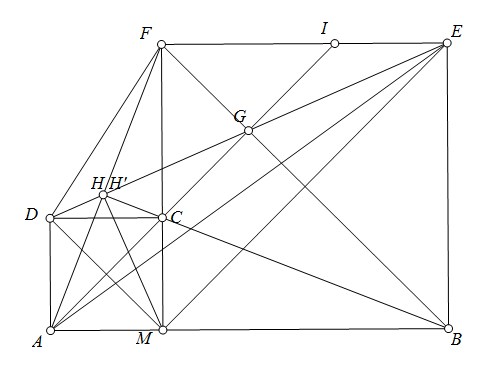
Bổ đề. Cho tứ giác $ABCD$ nội tiếp được đường tròn. Gọi $E,F$ lần lượt là các giao điểm của $AD$ và $BC$, $AB$ và $CD$. Gọi $I$ là giao điểm của phân giác hai góc $BFC,DEC$. $G,H$ lần lượt là trung điểm của $BD,AC$. Chứng minh rằng $G,H,I$ thẳng hàng.

Chứng minh. Xem tại đây

Quay trở lại bài toán.

Gọi $T$ là trực tâm của tam giác $AEF$.

Từ Bổ đề ta có được: $IK$ là $\text{Gauss}$

Theo tính chất đường thẳng $\text{Gauss}$ vuông góc với đường thẳng $\text{Steiner}$: $IK \perp HT$

Bài toán 181. Cho tam giác $ABC$ nhọn nội tiếp $(O;R)$ ,ngoại tiếp $(I;r).$ Gọi $x,y,z$ lần lượt là khoảng cách từ $O$ đến các cạnh của tam giác.

Chứng minh rằng $x+y+z= R+r.$

Bài toán 183. Đường tròn $(S)$ tiếp xúc với các cạnh $AB$ và $AC$ của tam giác $ABC$ nhọn tại $L,K$ và tiếp xúc với đường tròn ngoại tiếp tam giác ABC tại điểm M.

Chứng minh $MK$ đi qua điểm chính giữa cung $AC$ nhỏ của $(O).$

Bài toán 195. Tam giác $ABC$ có trực tâm $H$, $K$ là một điểm khác $H$ nằm trong tam giác. $H_1,H_2,H_3$ lần lượt là trực tâm tam giác $AHK, BHK, CHK$. $X,Y,Z$ là theo thứ tự là trung điểm $AH_1; BH_2; CH_3$. Chứng minh $X,Y,Z$ thẳng hàng.

Bài Toán 68. Cho đoạn thẳng AB, trên đó lấy điểm M. Trên cùng một nửa mặt phẳng bờ AB vẽ các hình vuông AMCD và BMFE. Đường thẳng DE cắt các đường thẳng AC và AF lần lượt tại G và H.

Chứng minh rằng: A, H, G, B cùng thuộc một đường tròn.

$\textbf{Lời giải Bài Toán 68}$

Gọi $I$ là giao điểm của $EF$ và $AG$ , $H'$ là giao điểm của $BC$ và $AF$

$\Rightarrow \triangle FCI$ là tam giác cân tại $F$ $\Rightarrow FC=FI \Rightarrow CD=CM=EI \Rightarrow GC=GI$

$\Rightarrow FG \perp CI \Rightarrow FG \perp AC$ và $FB \perp AC \Rightarrow F,B,G$ thẳng hàng

Ta có: $AM \perp AB; AG \perp BF$ $\Rightarrow BH' \perp AF$ $\Rightarrow ADH'C$ và $EFH'M$ nội tiếp 

$\Rightarrow DH'A = EH'F = 45^{\circ}$ $D,H',E$ thẳng hàng $H \equiv H'$ $\Rightarrow \angle BHA = 90^{\circ}$

$\angle BHA =\angle BGA = 90^{\circ}$  $\Rightarrow A, H, G, B$ cùng thuộc một đường tròn.

Nhân tiện đây mình xin lỗi là mình gõ làm cho lệnh latex nó to quá, mình cũng chả hiểu tại sao ! Bạn nào rảnh thì chỉnh sửa giúp mình nhé !

Bạn xóa lệnh gõ \LARGE đi là nó nhỏ lại 

Bài toán 63 (IMO 2014):

Cho tam giác $ABC$ có $\widehat{BAC}$ là góc lớn nhất. Các điểm $P$, $Q$ thuộc cạnh $BC$ sao cho $\widehat{QBA}= \widehat{BCA}$ và $\widehat{CAP}=\widehat{ABC}$. Gọi $M,N$ lần lượt là điểm đối xứng của $A$ qua $P,Q$. Chứng minh rằng $BN$ và $CM$ cắt nhau trên đường tròn ngoại tiếp tam giác $ABC$.

$\textbf{Lời giải Bài Toán 63}$

Gọi $J$ là giao điểm của $BM$ và CN. Trên cạnh $BC$ lấy điểm $K$ sao cho $PK=PB$ $(K \neq B)$

Dễ thấy $ABMK$ là hình bình hành $\Rightarrow \angle AKB = \angle KBM$

$\triangle QAC \sim \triangle ABC ; \triangle PBA \sim \triangle ABC \Rightarrow \triangle QAC \sim \triangle PBA \Rightarrow \frac{AB}{AC}=\frac{AQ}{PB}=\frac{BK}{AN}$

$\Rightarrow \triangle ABK \sim \triangle CAN (c.g.c) \Rightarrow \angle CNA = \angle AKB = \angle KBM \Rightarrow $ Tứ giác $BQJN$ nội tiếp

$\Rightarrow \angle BJN = \angle BQN = \angle BAC \Rightarrow$ Tứ giác $ABCJ$ nội tiếp $\Rightarrow$ $J$ thuộc đường tròn ngoại tiếp $\triangle ABC$

Bạn NHoang1608 sửa đề lại thành như này mới đúng nhé: Cho tam giác $ABC$ có $\widehat{BAC}$ là góc lớn nhất. Các điểm $P$, $Q$ thuộc cạnh $BC$ sao cho $\widehat{PAB}= \widehat{BCA}$ và $\widehat{CAQ}=\widehat{ABC}$. Gọi $M,N$ lần lượt là điểm đối xứng của $A$ qua $P,Q$. Chứng minh rằng $BN$ và $CM$ cắt nhau trên đường tròn ngoại tiếp tam giác $ABC$.

$\boxed{\text{Bài Toán 61}}$ [Sưu tầm] Từ $A$ nằm ngoài đường tròn $(O;R)$ vẽ $2$ tiếp tuyến $AB,AC$ với đường tròn $(O)$ ($B,C$ là các tiếp điểm). Gọi $P,Q$ lần lượt là trung điểm của $AB,AC$. Từ điểm $M$ bất kỳ thuộc cạnh $PQ$ kẻ tiếp tuyến $MD$ của đường tròn. Chứng minh rằng: $MA=MD$

$\textbf{Lời giải Bài Toán 61} $

Gọi $H$ là giao điểm của $OA$ và $BC$

$OD^2=OB^2=OH.OA$ $\Rightarrow$ $OD$ là tiếp tuyến đường tròn $(O)$ 

$\Rightarrow M$ là tâm đường tròn ngoại tiếp tam giác $ADH$ $\Rightarrow MA=MD$

Bài 83: (Sưu tầm)

Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Lời giải bài toán 83.

Bổ đề: Cho tam giác $MNP$.$H$ là trung điểm của $BC$.$N_1,P_1$ lần lượt là chân đường vuông góc hạ từ $N,P$. Chứng minh rằng $(HNP_1),(HPN_1)$ và $MH$ đồng quy

Chứng minh. Giả sử $K_1,K_2$ lần lượt là giao điểm của MH với $(HNP_1),(HPN_1)$

Theo tính chất cát tuyến: $MP_1.MN=MK_1.MH;MN_1.MP=MK_2.MH$

$MP_1.MN=MN_1.MP$ $\Rightarrow MK_1.MH=MK_2.MH$ $\Rightarrow MK_1=MK_2$ $\Rightarrow K_1 \equiv K_2$

$\Rightarrow$ $(HNP_1),(HPN_1)$ và $MH$ đồng quy 

Quay trở lại bài toán.

Gọi $I$ là giao điểm của $BC$ và $B_1C_1$ 

Từ bổ đề trên ta có được $A,P,O$ thẳng hàng

$\angle CB_1P= \angle BOP = \angle AC_1P$ $\Rightarrow$ $A,B_1,P,C_1$ cùng nằm trên $1$ đường tròn

Lại có $A,B_1,M,C_1$ nằm trên đường tròn đường kính $AM$ 

$\Rightarrow A,B_1,M,P,C_1$ cùng nằm trên đường tròn đường kính $AM$ 

$\Rightarrow \angle APM =90^{\circ}$ $\Rightarrow MP \perp OA$ $(1)$

Theo định Lý $\text{Brocard}$ ta có: $O$ là trực tâm của tam giác $AMI$ $\Rightarrow IM \perp OA$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow I,M,P$ thẳng hàng

Vậy Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Lời giải Bài Toán 91.

Bổ đề. Cho tam giác $XYZ$ có đường cao $XT$. $R$ là tâm đường tròn ngoại tiếp tam giác $XYZ$. Chứng minh rằng  $\angle RXZ = \angle YXT$

Chứng minh. Gọi $J$ là giao điểm thứ hai của $XR$ với đường tròn $(R)$

Dễ dàng chứng minh được $\triangle XYT \sim \triangle XJZ$ $\Rightarrow \angle RXZ = \angle YXT$

Quay trở lại bài toán.

Kẻ $AH$ vuông góc với $BC$ $(H  \in BC)$

Từ $L$ là trung điểm của $OK$ $\Rightarrow LO=LC=LB=LK$

$\Rightarrow \triangle OLC$ cân tại L $\Rightarrow \angle COL = \angle OCL$

Dễ thấy $\triangle OCI$ cân tại $C$ $\Rightarrow \angle OIC = \angle IOC = \angle OCL$

$\Rightarrow \triangle OCI \sim \triangle OLC \Rightarrow OI.OL=OC^2=OA^2$

$\Rightarrow \triangle OAI \sim \triangle OLA \Rightarrow \angle OAI = \angle OLA = \angle HAL (HA \parallel OL)$ $(1)$

Từ bổ đề trên ta có được $\angle BAH = \angle OAC$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow \angle HAL + \angle BAH = \angle OAI +  \angle OAC \Rightarrow \angle IAC = \angle LAB \Rightarrow \angle LAC = \angle IAB $

Mình đang có ý định viết tài liệu tổng hợp mấy bài Hình này, bạn nào viết chung thì trao đổi qua tin nhắn với mình :> .

Bài Toán 95.(Sưu tầm) Cho tam giác $ABC$ , có đường cao $AH$. $I$ là tâm đường tròn nội tiếp , $D$ là giao điểm của $(I)$ và $BC$. Kẻ $IN \perp AH$ $(N \in AH)$. Chứng minh rằng: $AI$ và $ND$ cắt nhau tại một điểm trên đường tròn ngoại tiếp tam giác $ABC$.

$\boxed{\text{Bài Toán 61}}$ [Sưu tầm] Từ $A$ nằm ngoài đường tròn $(O;R)$ vẽ $2$ tiếp tuyến $AB,AC$ với đường tròn $(O)$ ($B,C$ là các tiếp điểm). Gọi $P,Q$ lần lượt là trung điểm của $AB,AC$. Từ điểm $M$ bất kỳ thuộc cạnh $PQ$ kẻ tiếp tuyến $MD$ của đường tròn. Chứng minh rằng: $MA=MD$

Bài Toán 88.(Sưu tầm) Cho 4 điểm A,B,C,D theo thứ tự nằm trên một đường thẳng.Gọi $\omega_1,\omega_2,\omega_3,\omega_4$ lần lượt là đường tròn bất kì qua các cặp điểm $(A,B),(B,C),(C,D),(D,A)$. $X,Y,Z,T$ lần lượt là giao điểm thứ hai của các cặp đường tròn $\omega_1​$ và $\omega_2$,$\omega_2$ và $\omega_3$,$\omega_3$ và $\omega_4$,$\omega_4$ và $\omega_1$.Khi đó $X,Y,Z,T$ cùng nằm trên một đường tròn

Bài Toán 85.(Sưu tầm) Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ tiếp xúc với $AB,AC$ lần lượt tại $M,N$ và tiếp xúc với $(O)$ tại $J$.Chứng minh rằng $JN$ đi qua điểm chính giữa cung $AC$

Bài toán 58: (TST Đà Nẵng 2016-2017). 

Cho tam giác $ABC$ nhọn nội tiếp $(O)$, $H$ là trực tâm tam giác. Đường thẳng qua $A$ vuông góc với $OH$ cắt $BC$ tại $D$. $K,L$ lần lượt là tâm đường tròn ngoại tiếp tam giác $ADB,ADC$.

       1. Chứng minh $A,K,L,O$ thuộc một đường tròn gọi là $(S)$.

       2. $AH$ cắt $(S)$ tại điểm $E$. $F$ đối xứng với $E$ qua $BC$. Chứng minh rằng: $HA=HF$.

Lời giải đã có ở đây

Bài 47: (Thi thử KHTN đợt 3 vòng 2 2016-2017).

Cho tam giác nhọn $ABC$ nội tiếp trong đường tròn $(O)$. Giả sử có điểm $P$ nằm trên cung $BC$ không chứa diểm $A$ và các điểm $E,F$ lần lượt nằm trên các đoạn thẳng $CA,AB$ sao cho $CE=PB, BF=PC$. Gọi $M$ là trung điểm của $EF$.

        a) Chứng minh rằng $MB\perp MC$.

        b) Đường tròn ngoại tiếp tam giác $AEF$ cắt $(O)$ tại $G$ ($G$ khác $A$). Chứng minh rằng $PG$ đi qua trung điểm đoạn thẳng $BC$.

Lời giải xem tại đây

Bài 48. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ đi qua $B$ và $C$ cắt $AB,AC$ theo thứ tự $M$ và $N$. Đường tròn ngoại tiếp tam giác $AMN$ cắt $(O)$ tại điểm thứ $2$ là $D$. Chứng minh rằng: $AD \perp DI$

$\boxed{43}$ Cho tam giác $ABC$ nhọn nội tiếp $(O)$ các đường cao $BE,CF,AD$ cắt nhau tại $H$, lấy $H$' đối xứng với $H$ qua $BC$, $H'E$ cắt $(O)$ tại $M$. Chứng minh $BM$ đi qua trung điểm $EF$.

1 cách khác cho bài 43 

$\boxed{\text{Lời giải bài 43}}$

Gọi $I$ là giao điểm của $BM$ và $EF$. Từ $E$ kẻ đường vuông góc với AB tại $K$

Bổ đề: $H'$ đối xứng với trực tâm $H$ qua $BC$

$\Rightarrow H' $ thuộc đường tròn tâm $(O)$ 

Tứ giác $BCEF$ nội tiếp $\Rightarrow \widehat{FEB}= \widehat{BCF}$

$\widehat{BCF} = \widehat{BAD}$ (cùng phụ $\widehat{ABC}$)

$\widehat{BAD}=\widehat{BMH'}$ (cùng chắn cung $BH'$)

$\Rightarrow \widehat{FEB}=\widehat{BMH'}$

$\Rightarrow \Delta BEI \sim \Delta BME $ (g.g)$\Rightarrow BE^2 = BI.BM$

Hệ thức lượng: $BE^2=BK.AB$

$ \Rightarrow BI.BM=BK.AB$ $\Leftrightarrow \dfrac{BK}{BM} = \dfrac{BI}{AB}$

$\Rightarrow \Delta BIK \sim \Delta BAM \Rightarrow \widehat{BKI} = \widehat{BMA}$

Mà $\widehat{BMA}=\widehat{BCA}=\widehat{AFE}$ $\Rightarrow \widehat{BKI}=\widehat{AFE}$ hay $\widehat{FKI}=\widehat{KFI}$

$\Rightarrow \Delta KFI$ là tam giác cân tại I

$\Rightarrow IK=IF$ $\Rightarrow IK=IF=IE=\dfrac{1}{2}EF$

Vậy $BM$ đi qua trung điểm $I$ của $EF$

$\boxed{43}$ Cho tam giác $ABC$ nhọn nội tiếp $(O)$ các đường cao $BE,CF,AD$ cắt nhau tại $H$, lấy $H$' đối xứng với $H$ qua $BC$, $H'E$ cắt $(O)$ tại $M$. Chứng minh $BM$ đi qua trung điểm $EF$.

Rất cám ơn các em đã đóng góp nhiệt tình cho topic với đặc biệt là nhiều đề hình hay của THPT chuyên KHTN. Vừa qua mình bị một số việc quan trọng phải xử lý nên không thường xuyên qua được. Giờ mọi việc tạm ổn, mình sẽ cố gắng quay lại thường xuyên hơn. Xin đóng góp một bài hình khá mới cho THCS của mình

 

Bài toán 51. Cho tam giác $ABC$ có $D$ nằm trên đoạn $BC$. $(K),(L)$ lần lượt là đường tròn ngoại tiếp các tam giác $ADB,ADC$. $DR,DQ$ là đường kính của $(K),(L)$. $P$ thuộc đoạn $KL$ sao cho $DP\perp BC$. $QP,RP$ lần lượt cắt $BC$ tại $M,N$. Chứng minh rằng $\angle MAN=\angle BAC$.

 

Gọi $E,F$ lần lượt là trung điểm $KB,LC$ $\Rightarrow$ $J$ là giao điểm của $EF$ và $PD$

Gọi $X,Y$ lần lượt là giao điểm của $LJ,KJ$ với đường thẳng $BC$

Gọi $G,H$ là lần lượt là trung điểm $DB,DC$

Gọi $I$ là giao điểm của $KL$ và $BC$

Theo bổ đề $\text{Eriq}$ thì: $JP=JD$

Áp dụng định lý $\text{Menelaus}$ vào tam giác $PDI$ ta có:

$\dfrac{LP}{LI}.\dfrac{IX}{XD}.\dfrac{JP}{JD}=1$

$\Rightarrow \dfrac{LP}{LI}=\dfrac{XD}{IX}$

$\Rightarrow \dfrac{XD}{IX} = \dfrac{HI}{HD}$

$\Rightarrow (I,X,D,H)=-1$ (hàng điểm điều hòa) với $SD \perp LI$

$\Rightarrow SD$ là tia phân góc của $\angle XSH$ $(1)$

Chứng minh tương tự: $SD$ là tia phân giác của $\angle GSY$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow \angle XSG = \angle YSH$

Dễ dàng chứng minh được: $\angle XSG = \angle MAB$ , $\angle YSH = \angle NAC$

$\Rightarrow  \angle MAB = \angle NAC$

$\Rightarrow \angle MAN=\angle BAC$ 

Bài 50: Thi thử vào Chuyên Toán ĐHSP 2014-2015.

Cho đường tròn $(O)$ có dây cung $BC$ không là 1 đường kình. Gọi $A$ là điểm chính giữa cung lớn $BC$. Các tiếp tuyến của $(O)$ tại $B,C$ cắt nhau tại $S$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $M$ là trung điểm của$CH$. $AM$ cắt $(O)$ tại $N$.

a) Gọi  giao diểm của $SA$ và $BC$ là $D$. Chứng minh rằng: $CMDN$ nội tiếp.

b) Tia $SA$ cắt $(O)$ tại điểm thứ hai là $E$ Chứng minh rằng: $CE//SA$.

c) Chứng minh rằng: $CN$ chia đôi $SD$.

a) $MC=MH ; DB=DC \Rightarrow DM \parallel AB \Rightarrow \angle BAN=  \angle DMN$

 và $ \angle BAN =  \angle DCN$ (cùng chắn cung $BC$)

$\Rightarrow \angle DMN = \angle DCN$

$\Rightarrow$ Tứ giác $CMDN$ nội tiếp

b) Bạn xem lại đề câu này nhé

c) Gọi $J$ là giao điểm của $CN$ và $SA$

Theo hệ thức lượng: $DJ^2 = JN.JC$ $(1)$

$\angle SBN = \angle BAN = \angle BCN = \angle JDN$

$\Rightarrow$ Tứ giác $BDNS$ nội tiếp

$\Rightarrow \angle DSN = \angle DBN = \angle NAC = \angle JCS$

$\Rightarrow \Delta JSN \sim \Delta JCS$ $(g.g)$

$\Rightarrow JS^2 = JN.JC$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow$ $JS=JD$

$\Rightarrow$ $CN$ chia đôi $SD$.

$\boxed{\text{Bài Toán 59}}$[Nguyễn Quang Trung] Cho tam giác $ABC$ đường cao $AD,BE,CF$ đồng quy tại $H$. Hạ $HG$ vuông góc với $EF$. $I$ thuộc $BE$ sao cho $GI \parallel BC$. $J$ là tâm đường tròn ngoại tiếp tam giác $IEF$. Chứng minh rằng $3$ điểm $J,G,D$ thẳng hàng.

Bài toán 57: (Toán học tuổi trẻ).

Cho tam giác nhọn $ABC$, tia phân giác trong của góc $BAC$ cắt $BC$ tại $D$. Gọi $E,F$ thứ tự là hình chiếu vuông góc của $D$ trên $AB$ và $AC$,$K$ là giao điểm của $CE$ và $BF$, $H$ là giao điểm của $BF$ với đường tròn ngoại tiếp tam giác $AEK$. Chứng minh rằng $DH$ vuông góc với $BF$.

$\textbf{Lời giải Bài Toán 57:}$

Gọi $L$ là giao điểm của $AK$ và $BC$, $L'$ là đường cao hạ từ $A$ xuống $BC$

Theo định lý $\text{Ceva}$ ta có: 

$BK.BH=BE.BA$ và $\Delta BDE = \Delta BAL (g.g) \Rightarrow BE.BA=BL.BD$

$\Rightarrow BK.BH=BL.BD$

$\Rightarrow \Delta BLK = \Delta BHD$

$\angle BHD = \angle BLK =90^0$ Hay $DH \perp BF$

Bài toán 53 (Thi thử vào chuyên Toán KHTN 2012). Cho tam giác $ABC (AB<AC)$ nội tiếp đường tròn $(O)$. Phân giác góc $\widehat{BAC}$ cắt $(O)$ tại điểm $D$. Lấy $E$ đối xứng $D$ qua $O$. Gọi $F$ là 1 điểm thuộc cung $BD$ không chứa $A,C$ của $(O)$, $EF$ cắt $BC$ tại $G$. Lấy $H \in AF: GH//AD$. Chứng minh rằng: $HG$ là phân giác góc $BHC$.

Vẽ đường tròn $(I)$ ngoại tiếp $\Delta AHB$ cắt $AB$ và $AC$ lần lượt tại $M$ và $N$. Vẽ đường tròn $(S)$ ngoại tiếp $\Delta AMN$. 

Gọi $H'$ là giao điểm của $SI$ và đường tròn $(I)$. 

Từ $\text{Bài Toán 48}$ ta có được bổ đề sau: Tứ giác $AOBS$ là hình bình hành 

Dễ dàng chứng minh được $H'G \parallel AD$ , mà $HG \parallel AD$ $\Rightarrow H \equiv H'$

$\Rightarrow HG$ là phân giác góc $\angle BHC$

Bài 17 (Azerbaijan Junior Mathematical Olympiad). Với $x,\,y,\,z$ là ba số thực khác $0.$ Chứng minh rằng $$\sqrt {x^2+\frac {1}{y^2}}+ \sqrt {y^2+\frac {1}{z^2}}+ \sqrt {z^2+\frac {1}{x^2}}\geq 3\sqrt {2}. $$

 

 

Bài 17:

Áp dụng bất đẳng thức Minkowxki ta có:

\[\sqrt {{x^2} + \frac{1}{{{y^2}}}}  + \sqrt {{y^2} + \frac{1}{{{z^2}}}}  + \sqrt {{z^2} + \frac{1}{{{x^2}}}}  \ge \sqrt {{{\left( {x + y + z} \right)}^2} + {{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2}} \]

Áp dụng bất đẳng thức AM - GM ta có:

\[\sqrt {{{\left( {x + y + z} \right)}^2} + {{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2}}  \ge \sqrt {9\sqrt[3]{{{x^2}{y^2}{z^2}}} + 9\frac{1}{{\sqrt[3]{{{x^2}{y^2}{z^2}}}}}}  \ge 3\sqrt 2 \]

Dấu đẳng thức xảy ra khi và chỉ khi: x = y = z = 1

$\LaTeX$

Bài 25: Jack Garfunkel

Cho $a, b, c \geq 0$. Chứng minh rằng:

$$\frac{a^{2}+b^{2}+c^{2}}{ab+bc+ca} + \frac{8abc}{(a+b)(b+c)(c+a) } \geq 2$$

 Mình đăng bài này có mục đích trước hết các bạn hãy giải bài này xong. Sau đó mình sẽ làm trội bài này bằng 1 bổ đề rất rất chặt

Có tất cả 6 cách chứng minh cho Bài Toán này. Xem tại đây

Nguồn: Lê Khánh Sỹ