Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 5 tháng 10 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán mới,
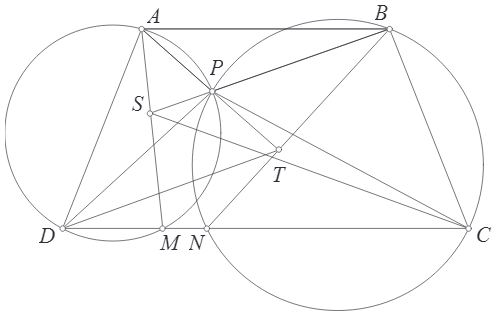
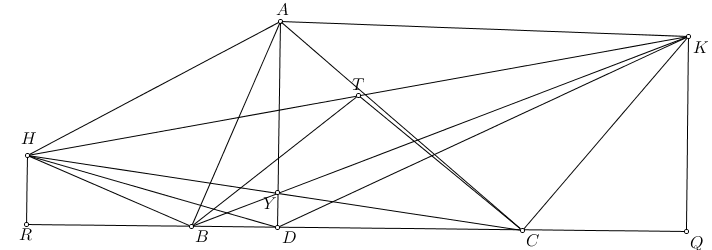
Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Tiếp tuyến tại $B,C$ của $(O)$ cắt nhau tại $T$. $D$ là một điểm trên cạnh $BC$. $TD$ cắt $(TBC)$ tại $P$ khác $T$. $K$ thuộc $BC$ sao cho $AK\parallel PD$. $L$ thuộc $AK$ sao cho $DL\parallel AP$. Chứng minh rằng trục đẳng phương của đường tròn $(DKL)$ và $(TBC)$ đi qua giao điểm của $KP$ và $AD$.
Hình vẽ bài toán

 Đã gửi bởi
Đã gửi bởi