Chứng minh rằng:
$(abc+1)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})(\frac{a}{c}+\frac{c}{b}+\frac{b}{a}) \geq a+b+c+6 \forall a,b,c > 0 $

$\sqrt{2-x^2} + \sqrt{2- \frac{1}{x^2}} = 4- (x+ \frac{1}{x})$

Thế túm lại đề là $ x - \frac{1}{x} $hay $x + \frac{1}{x} $ tarzan ui

Bài 1:Giải bất PT:
$ \sqrt{3x-5} + \sqrt[3]{5x-7} + \sqrt[4]{x+13} + \sqrt[5]{7x+11} > 8$

Bài 2: Giải PT
1, $ x^2- 3x+1 = - \dfrac{\sqrt{3}}{3} \sqrt{ x^4+x^2+1}$
2, $ \sqrt{x-1} + \sqrt{x^3+x^2+x+1} = 1+ \sqrt{x^4-1}$

$1) \left ( 3-x \right )\sqrt[3]{\frac{3-x}{x-1}} + \left (x-1 \right )\sqrt[3]{\frac{x-1}{3-x}} =2$

LG:
Đặt: $ a = \sqrt[3]{3-x} ; b = \sqrt[3]{x-1} \Rightarrow a^3+b^3=2$
Ta có pt:
$\dfrac{a^4}{b} + \dfrac{b^4}{a} = a^3+b^3$
PT này đến đây nhân chéo xong là giải đc thui ^v^

Bài 1: Giải PT:
$ 1, \sqrt{4-3\sqrt{10-3x}} = x-2$
$ 2, 4x^2- 2x-10 = 2 \sqrt{8x^2-6x-10} $
$ 3, x^3 - 3x^2 - 8x+40-8 \sqrt[4]{4x+4} = 0$
$ 4, 2\sqrt{(2-x)(5-x)} = x+ \sqrt{(2-x)(10-x)}$
$ 5, \sqrt[3]{x^2+4} = \sqrt{x-1}+2x-3$

Bài 2: PT $ x^3 - 3x^2+4 = \sqrt{3+2x-x^2}$ có bao nhiêu nghiệm
Bài 3: CMR PT luôn có nghiệm $\forall m \geq 0 $:
$ x^2 + ( m- \dfrac{5}{3})\sqrt{x^2+4} +2 - m ^3 = 0$

Giải hệ PT sau:

$\left\{\begin{matrix}(1+ \dfrac{1}{x+y}).\sqrt{3x} = 2
& \\(1- \dfrac{1}{x+y}).\sqrt{7y} = 4\sqrt{2}
&
\end{matrix}\right.$
Sorry mọi người t gõ nhầm! Hì.

Cho $ a, b, c > 0$. CMR:
$\sqrt{\dfrac{a+b}{c}} + \sqrt{\dfrac{b+c}{a}} + \sqrt{\dfrac{a+c}{b}} \geq 2 ( \sqrt{\dfrac{c}{a+b}} + \sqrt{\dfrac{a}{b+c}} + \sqrt{\dfrac{b}{a+c}}) $

Bài 2 ;
$\dfrac{a_1}{a_1 + b_1} + \dfrac{a_2}{a_2 + b_2} +... +\dfrac{a_n}{a_n + b_n} \ge \sqrt[n]{\dfrac{a_1a_2...a_n}{(a_1 + b_1)...(a_n + b_n)}}$ Tương tự, bạn áp dụng cho bộ b. cộng hai cái này lại, suy ra ĐPCM.

thank b

Sử dụng 1 đẳng thức hiển nhiên :
$$\dfrac{n-1}{n!}=\dfrac{1}{(n-1)!}-\dfrac{1}{n!}$$
Ta có:
$$VT=\sum\limits_{i=2}^{n}\left(\dfrac{i-1}{i!} \right)=\sum\limits_{i=2}^{n}\left[\dfrac{1}{(i-1)!}-\dfrac{1}{i!} \right]=1-\dfrac{1}{n!}<1=VP;\forall n \in \mathbb{N};n \ge 2$$
Xong.

Thank b

Bài 1: Chứng minh rằng: $\dfrac{1}{2!} + \dfrac{2}{3!} + \dfrac{3}{4!} + ... + \dfrac{n-1}{n!} < 1 $ $\forall n \in N; n \geqslant 2$

Bài 2: Cho 2n số dương a₁, a₂, ..., a_n và b₁, b₂, ..., b_n. CMR:

chứng minh rằng: $1.3.5....(2n - 1) < n^{n}$

Mình làm câu a minh hoạ :1.$ 1\dfrac{1}{2^2} . \dfrac{1}{3^3} ...\dfrac{1}{n^n} \le \dfrac{(n+1)n}{2}( 1 + \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{3} + \dfrac{1}{3} + ... + \dfrac{1}{n} + \dfrac{1}{n} +... +\dfrac{1}{n})^{\dfrac{(n + 1)n}{2}$ Đến đây thì bạn đã hiểu ?

Thank bạn

bài 3 : Khai triển vế trái, ta có $$1 + \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} +\dfrac{1}{ab} + \dfrac{1}{bc} + \dfrac{1}{ca} + \dfrac{1}{abc} \ge 1 + \dfrac{3}{a + b + c} + \dfrac{9}{(a + b + c)^2} + \dfrac{27}{(a + b + c)^3} \ge (1 + \dfrac{3}{k})^3.$$
Bài 2 : $a + b + c = \dfrac{(m + n + k)(a + b + c)}{m + n + k} + ... = \dfrac{ ma +nb + kc }{m + n + k} +... \ge $. $\sqrt[m + n + k]{a^m.b^n.c^k} +...$
Từ đây suy ra đpcm.
Bài 4: Ta chỉ cần sử dụng bđt Becnuli thôi.vì m > n nên $(1 + \dfrac{1}{m})^{\dfrac{m}{n}} > 1 + \dfrac{1}{m} . \dfrac{m}{n}$ suy ra đpcm
Bài 1 cũng tương đối dễ, ta chỉ cần dùng côsi cho $\dfrac{(n + 1)n}{2} số$

Bài 1 dùng côsi cho $\dfrac{(n + 1)n}{2} số$ ntn zậy?

Bài 1 dùng côsi cho $\dfrac{(n + 1)n}{2} số$ ntn zậy?

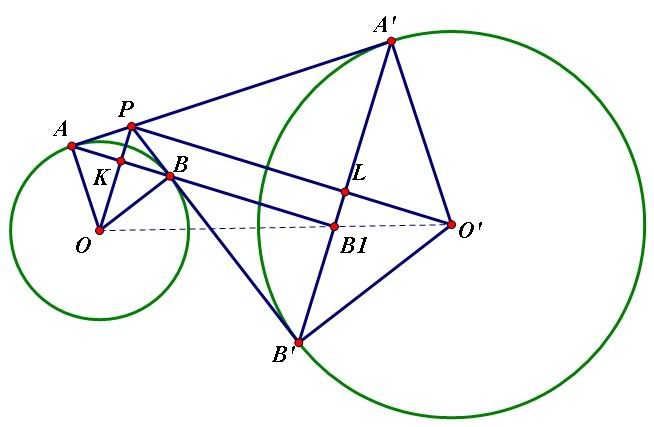
À, vì $\angle OKB_1=\angle OPO'=90^o$ mà bạn

Uk nhi?
K danh' vuong goc nen wen mat'
Thank ban

Gọi K là giao điểm của AB và OP; L là giao điểm của A'B' và PO'.
$\vartriangle OPA \sim \vartriangle PO'A'$ và AK, A'L là các đường cao tương ứng nên
$\dfrac{OK}{OP}=\dfrac{PL}{PO'}$
Lại có:$PL=KB_1$ (do $PLB_1K$ là hình chữ nhật)
nên $\dfrac{OK}{OP}=\dfrac{KB_1}{PO'}$
$\Rightarrow \vartriangle OKB_1 \sim \vartriangle OPO'(c.g.c) \Rightarrow \angle KOB_1=\angle POO' \Rightarrow Q.E.D$

Mjnh k hieu? vi sao $ \vartriangle OKB_1 \sim \vartriangle OPO'(c.g.c) $
Neu la cgc vi $\dfrac{OK}{OP}=\dfrac{KB_1}{PO'}$ va $\widehat{O'OP}= \widehat{B1OK}$ thi co le la k dung, vi O, B1, O' chua thang hang
Neu sai thi bo? wa nha'

cho ABC vuông tại A,AB>AC, lầy điểm M bất kì thuộc BC, Trên nửa mặt phẳng bờ BC có chứa A vẽ hai tia Bx,Cy vuông góc với BC, vẽ đường thẳng đi qua A và vuông góc với AM, cắt Bx,Cy lần lượt tại E,F
a.chứng minh tam giác AMF vuông
b.H là hình chiếu của A trên BC.cho BC=20cm,AC=15cm,MH=5cm,tính HB, HC
c.tính diện tích tam giác MEF
d.Xác định vị trí diểm M trên BC đẻ diện tích tam giác AMF gấp đôi diện tích tam giác ABC
giúp e với nha, thanks

Ta lam` theo de` bai` da~ sua? nhe'
T la mem moi' nen chua pjt ve~ hinh`, ban thong cam? ve~ ra nhap roi` xem nhe'

a. De dang cm dc tu giac $ AFCM$ noi tiep $\widehat{ACB} = \widehat{MFE} $
CM tuong tu ta dc $\widehat{ABC} = \widehat{MEF} $
tam giac $ ABC$ dong dang vs tam giac $ MEF$
tam gic MEF vuong o M
b,c dua vao he thuc luong va ti so dong dang se tinh dc. Fai kien tri vi so hoi le?
d. tam giac $ ABC$ dong dang vs tam giac $ MEF$
$\dfrac{S( EMF)}{S(BAC)} = \dfrac{EF^2}{BC^2} = 2$
$ EF= BC \sqrt{2} $
Ma $ S(MEF)= \dfrac{AM.EF}{2} $
$ S(ABC)= \dfrac{AH.BC}{2} $
$ EF.AM=2AH.BC$
$ \sqrt{2}BC.AM= \sqrt{2}BC . \sqrt{2}AH$
$ \dfrac{AH}{AM} = \dfrac{ \sqrt{2} }{2} $
Mat khac $ \dfrac{AH}{AM} = Sin \widehat{AMC} $
$\widehat{AMC}= 45$
M thuoc BC sao cho $\widehat{AMC}= 45$ la vi tri can tim

cho ABC vuông tại A,AB>AC, lầy điểm M bất kì thuộc BC, Trên nửa mặt phẳng bờ BC có chứa A vẽ hai tia Bx,Cy vuông góc với BC, vẽ đường thẳng đi qua A và vuông góc với AM, cắt Bx,Cy lần lượt tại E,F
a.chứng minh tam giác AMF vuông
b.H là hình chiếu của A trên BC.cho BC=20cm,AC=15cm,MH=5cm,tính HB, HC
c.tính diện tích tam giác MEF
d.Xác định vị trí diểm M trên BC đẻ diện tích tam giác AMF gấp đôi diện tích tam giác ABC
giúp e với nha, thanks

Theo t thi de k dung thi fai?
Chac la the nay
cho ABC vuông tại A,AB>AC, lầy điểm M bất kì thuộc BC, Trên nửa mặt phẳng bờ BC có chứa A vẽ hai tia Bx,Cy vuông góc với BC, vẽ đường thẳng đi qua A và vuông góc với AM, cắt Bx,Cy lần lượt tại E,F
a.chứng minh tam giác EMF vuông
b.H là hình chiếu của A trên BC.cho BC=20cm,AC=15cm,MH=5cm,tính HB, HC
c.tính diện tích tam giác MEF
d.Xác định vị trí diểm M trên BC đẻ diện tích tam giác EMF gấp đôi diện tích tam giác ABC

Bài 1:

Bài 2:

Bai 1:
De dang cm dc tu giac ADFC noi tiep $\widehat{CDF} = \widehat{CAF}$ (2 goc noi tiep cung chan cung FC)
Ma $ \widehat{CAF}= \widehat{CBK}$( 2 goc noi tiep cung chan cung CK cua (O))
$\widehat{CDF} = \widehat{CBK}$
Ma 2 goc nay o vtri dong vi
$DF // BK$
Goi N la trung diem cua AC $ ND= NF= \dfrac{AC}{2} $(1)
Xet tam giac ABC co MN la duong TB $ MN // AB$
Mat khac: $ AB \perp BK $ vi $\widehat{ABK} = 90 $
$ MN \perp DF$(2)
Tu (1) va (2) MN la trung truc cua DF
CM tuong tu ta duoc M la giao 3 duong trung truc cua tam giac DEF
hay M la tam duong tron ngoai tiep tam giac DEF

Rất tiếc bài làm của bạn không đúng

K dung cho nao vay?

Làm tiếp câu 3.
a,Ta có:$\dfrac{1}{1+a^{2}+b^{2}}+\dfrac{1}{2ab}=\dfrac{1}{2-2ab}+\dfrac{1}{2ab}\geq \dfrac{4}{2}=2$.
b,$\dfrac{1}{a^{2}+b^{2}}+\dfrac{1}{ab}+4ab=\dfrac{1}{1-2ab}+\dfrac{1}{2ab}+\dfrac{1}{2ab}+4ab\geq \dfrac{4}{1}+\dfrac{1}{4ab}+2\geq 7$.

Fan a lam the k dc dau vj k xay ra dau "="
E lam thu?
$(a+b)^2 $ $ 2(a^2+b^2) $ $1 $$ 2(a^2+b^2)$ $1+a^2+b^2$ $3(a^2+b^2)$
$\dfrac{1}{1+a^{2}+b^{2}}$ $\dfrac{1}{3(a^{2}+b^{2})}$
Dat $A=\dfrac{1}{1+a^{2}+b^{2}}+\dfrac{1}{2ab}$
$A$ $\dfrac{1}{3(a^{2}+b^{2})}+ \dfrac{1}{6ab} +\dfrac{1}{3ab} $
ap dung bdt $ \dfrac{1}{x} + \dfrac{1}{y} $ $ \dfrac{4}{x+y} $ ta co:
$\dfrac{1}{3(a^{2}+b^{2})}+ \dfrac{1}{6ab} $ $ \dfrac{1}{3} ( \dfrac{4}{a^2+b^2+2ab}) = \dfrac{1}{3} . \dfrac{4}{(a+b)^2} = \dfrac{4}{3} $
$ab$ $ \dfrac{(a+b)^2}{4} = \dfrac{1}{4} $
$ \dfrac{1}{3ab} $ $ \dfrac{4}{3} $
$A$ $ \dfrac{8}{3} $
Dau "=" xay ra $a=b=0.5$