Lời giải bài 172 : 

Trước tiên ta chứng min bổ đề sau : 

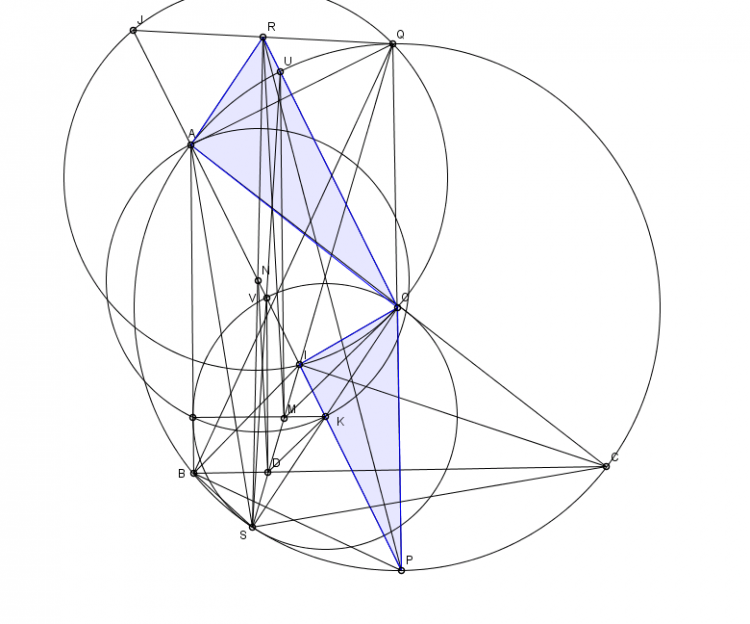
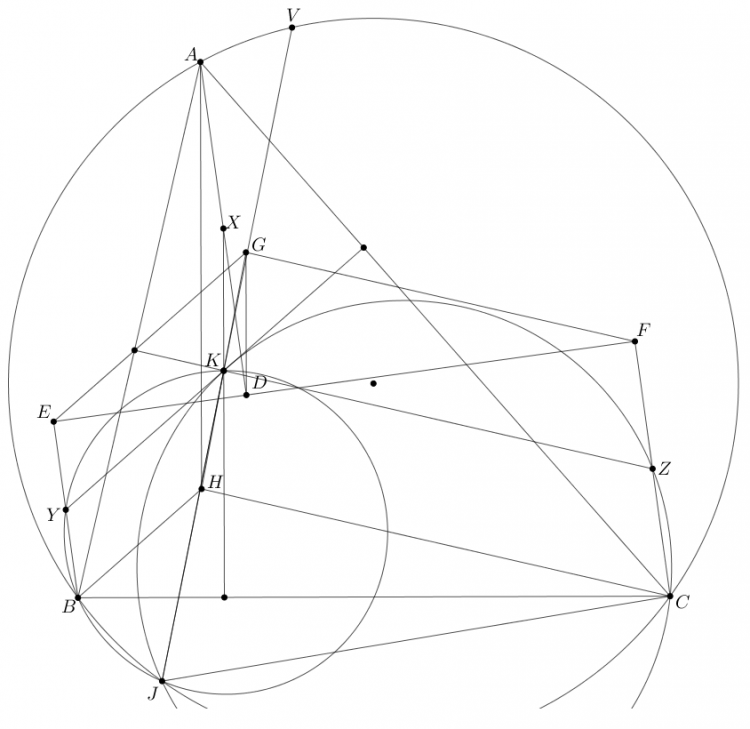
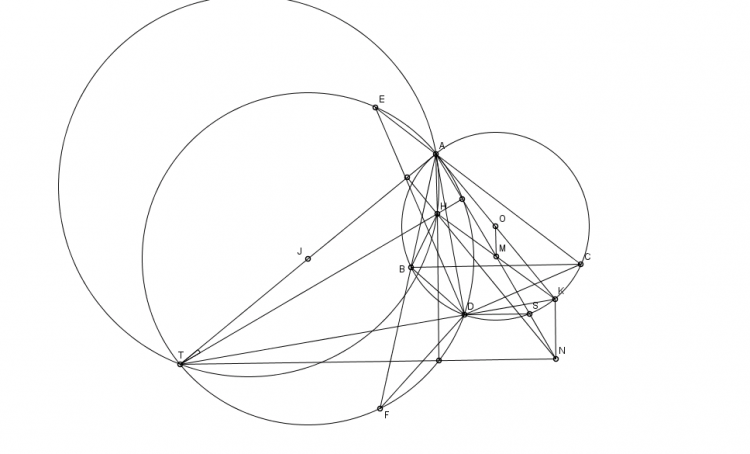
Bổ đề : Cho $\triangle ABC$. Đường tròn $(X)$ bất kì qua $A$ tiếp xúc với đường tròn Euler cắt $AB,AC$ tại $M,N$. Chứng minh rằng đường tròn $(XMN)$ tiếp xúc với đường trung bình của $\triangle ABC$

 

Chứng minh : Xét phép nghịch đảo $I^A_k$, bài toán trên trở thành : Cho $\triangle ABC$ nội tiếp $(O)$. Đường thẳng bất kì tiếp xúc $(BOC)$ cắt $CA,AB$ tại $M,N$. $D$ đối xứng $A$ qua $MN$. Khi đí $(DMN)$ tiếp xúc $(O)$ ( đây chính là bài toán SMO 2016 ở đây https://www.artofpro...1220645p6102531 )

 

Áp dụng : Gọi $T$ là trung điểm $MH$

Theo định lý Menelaus ta có : $1 = \frac{\overline{DQ}}{\overline{DP}}.\frac{\overline{NP}}{\overline{NA}}.\frac{\overline{HA}}{\overline{HQ}}= \frac{\overline{DQ}}{\overline{DP}}.\frac{\overline{MP}}{\overline{MC}}.2=\frac{\overline{DQ}}{\overline{DP}}\frac{\overline{MP}}{\overline{MH}} \implies \frac{\overline{DQ}}{\overline{DP}}=\frac{\overline{MH}}{\overline{MP}}$ nên $MD \perp BC$

Ta có đường trung bình của $\triangle DAH$ tiếp xúc $(XMN)$ theo bổ đề, mà đường trung bình này chính là đường thẳng qua $T$ vuông góc $BC$ nên $(XMN)$ tiếp xúc đường thẳng cố định là đường qua trung điểm $MH$ vuông góc $BC$

Bài toán 173. Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$, $E$ là giao điểm của $AB$ với $CD$, $F$ là giao điểm của $AD$ với $BC$ . $(AEF)$ cắt $(O)$ tại $P$, $(CEF)$ cắt $O$ tại $Q$. $AC$ cắt $BD$ tại $I$. Chứng minh rằng $P,I,Q$ thẳng hàng.

Bài toán 177 :  Cho tứ giác nội tiếp $ABCD$, $AB$ cắt $CD$ tại $P$, $AD$ cắt $BC$ tại $Q$. Chứng minh rằng khoảng cách giữa trực tâm hai tam giác $APD$ và $AQB$ bằng khoảng cách giữa trực tâm hai tam giác $CQD$ và $BPC$

Bài toán 140 : (sách) Cho tứ giác $ABCD$ nội tiếp. Giả sử rằng tồn tại điểm $X$ để $\angle XAD = \angle XBA = \angle XCB = \angle XDC$. Chứng minh rằng tứ giác $ABCD$ điều hòa

Lời giải bài 176 : Gọi $M$ là chân đường phân giác ngoài góc $\angle A$, , $N$ là trung điểm $MD$, $NS$ là tiếp tuyến tới đường tròn $(T)$, $SD$ cắt trung trực $BC$ tại $X$, $R$ là trung điểm $BC$, $Z$ là trung điểm $SD$, $D'$ đối xứng $D$ qua $T$ suy ra $M,S,D'$ thẳng hàng.Gọi $L,L'$ là điểm chính giữa cung nhỏ , cung lớn $BC$. $K'$ đối xứng $L$ qua $K$ 

Ta có : $\frac{RX}{RD} = \frac{NZ}{ZD} = \frac{MD}{DD'}$ $= \frac{MD}{\frac{AD}{AL}.KL} = \frac{MD.AL}{AD.KL}= \frac{2R.AL}{AL'.K'L}$ $= \frac{2R}{K'L}.\frac{AL}{AL'} \implies RX =RD. \frac{2R}{K'L}.\frac{AL}{AL'} = RL .\frac{2R}{K'L}$ không đổi nên $X$ cố định

Thật vậy , ta có $DS.DX = DR.DM = DB.DC$ nên tứ giác $SBXC$ nội tiếp

Lại có $NS^2 = ND^2 = NM^2 = NB.NC$ nên $NS$ cũng là tiếp tuyến tới đường tròn $(SBXC)$. Mà điểm $X$ cố định nên đường tròn $(SBXC)$ cố định nên $(T)$ tiếp xúc với đường tròn cố định là $(BXC)$

 

Lời giải bài toán 121 : 

Gọi $J$ là giao điểm của $AP$ với $QR$. Do $AP \perp AQ$ nên $AP \parallel OR \implies R$ là trung điểm $OJ$.

$(K)$ tiếp xúc $(O)$ tại $S$. Gọi $U,V$ lần lượt là điểm chính giữa cung $AQ$ của $(O)$, cung $EF$ của $(K)$.

$SI$ là trung tuyến, $SA$ là đường đối trung $\triangle ESF$ nên $SA,SU$ đẳng giác trong $\angle ESF$. Từ đây ta có $S,U,V$ thẳng hàng

Thật vậy, theo bài toán 111 thì $DV \parallel UM$

Từ đây ta có $\triangle RUM$ và $\triangle NVD$ có các cặp cạnh tương ứng song song $\implies R,N,S$ thẳng hàng

Theo định lý Thales thì $\frac{OR}{KN} = \frac{OS}{KS} \implies OR = \frac{OS}{KS} . \frac{AK}{2}$

Ta có $\triangle QBP \sim \triangle AFK$ nên $\frac{QP}{PB} = \frac{AK}{KF} \implies \frac{2OS}{PB} = \frac{AK}{KS}$

Kết hợp 2 điều trên ta có $OR.PB = R^2 = OR.PI \implies \frac{OR}{OA} = \frac{OP}{PI} \implies \triangle RAO \sim \triangle OIP \implies \angle RQO = \angle RAO = \angle OIP$

$\implies RQ$ và $AP$ cắt nhau trên $(IOQ)$ tức là $JIOQ$ nội tiếp

Lại có $PR$ là trung tuyến $\triangle PQJ$ nên $PR$ là đường đối trung của $\triangle PIO$. Ta có điều cần chứng minh

P/s : bạn Bảo nhanh quá @@

Lời giải bài 139 : ( cách của em tính khá trâu bò ạ )

Ta có $(NE,AC) = -1$ nên $\frac{\overline{NA}}{\overline{NC}} = \frac{p-a}{p-c}$

Vậy tức là $\frac{\overline{NA}}{\overline{NA}+b}= \frac{p-a}{p-c}$ nên $\overline{NC} = |\frac{b(p-c)}{a-c}|$

Lại có $AQ = \frac{p-a}{cos \angle A}$ nên $CQ = b - AQ = b - \frac{p-a}{cos \angle A}$

Áp dụng đinh lý hàm cos có : $cos \angle A = \frac{b^2+c^2-a^2}{2bc}$

Vậy ta có $\overline{CQ} = \frac{b^3+bc^2-ba^2-b^2c-bc^2+abc}{b^2+c^2-a^2} = \frac{b^3-ba^2-b^2c+abc}{b^2+c^2-a^2}$

Vậy $\frac{\overline{CQ}}{\overline{CN}} = \frac{p-a}{cos \angle A}= |\frac{(b^3-ba^2-b^2c+abc)(a-c)}{(b^2+c^2-a^2)(p-c).b}| = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Tương tự ta có $\frac{\overline{BP}}{\overline{BM}} = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Nên $\frac{\overline{CQ}}{\overline{CN}}=\frac{\overline{BP}}{\overline{BM}}$ Áp dụng bổ đề E.R.I.Q  ta có trung điểm $MN,PQ,BC$ thẳng hàng

$\boxed { Lời \ giải \ bài \ 109 }$ Bài toán trên tương đương với bài toán sau 

Cho $\triangle ABC$ với $I,J$ lần lượt là tâm nội tiếp và tâm bàng tiếp góc $\angle A$. $K$ là trung điểm cung lớn $BC$. $JK$ cắt $(O)$ tại $X$. $E,F$ là hình chiếu của $X$ lên $IC,IB$. Chứng minh rằng trung điểm $EF$ nằm trên trung trực $BC$

 

Chứng minh : Gọi $M,N, G$ lần lượt là tâm bàng tiếp góc $\angle B, \angle C$, trung điểm $BC$. Ta cần chứng minh $KG$ đi qua trung điểm $EF$, $JK$ cắt $BC$ tại $T$

Ta sẽ chứng minh $\frac{BF}{CE} = \frac{BM}{CN}$

Ta có : $\frac{BF}{CE} = \frac{BF}{BX} .\frac{BX}{CX} . \frac{CX}{CE} = \frac{cos \angle FBX}{cos \angle ECX} . \frac{sin \angle XCB}{sin \angle XBC} = \frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC}$

Gọi $U,V$ là trung điểm cung lớn $AC,AB$ khi đó 

$\frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC} = \frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC} $

Bài tâp 42: Chứng mimh rằng a, b, c > 0, thì ta có 

$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}> \frac{2}{a} +\frac{2}{b}-\frac{2}{c}$

Điều cần chứng minh tương đương $a^2+b^2+c^2 \geq 2bc+2ca-2ab$ hay $(a+b-c)^2 \geq 0$

Bài này là của Gabriel Dospinesscu, có thể tham khảo cuốn Straight from the book, lời giải khá hay.

có thể dùng nội suy lagrange

Em xin phép giải câu hình 2 ạ 

a, Gọi $U$ là giao điểm của $KR$ với $BC$

Ta có $KT.KF = KB^2 $ nên $\angle KTB = \angle KBF = \angle KAF$. Suy ra $ADFT$ nội tiếp. Khi đó ta có $LD.LT = LF.LA = LB .LC = LP.LQ$ nên tứ giác $TPDQ$ nội tiếp

Lại có $KR.KU = KC^2$ nên tứ giác $ADRU$ nội tiếp. Và $KQ^2 = KC^2 = KD.KA$ nên ta có $\angle DUR = \angle DAR = \angle KQD = \angle PTD$. Từ đây suy ra $KR \parallel TP$

b,Gọi $M$ là giap điểm của $PK$ với $(O)$.Ta có $KL.KM = KB^2 = KP^2 = KQ^2$ nên $(ML,PQ) = -1 = A(ML,PQ) = A(MF,ER) = (MF,ER) = K(MF,ER) \implies KE$ chia đôi $TP$

 

Lời giải bài đa thức

Thế $a = x+1,b = -2x-1,c = -2x-3$, khi đó ta có $P^2(x+1)+P^2(-2x-1)+P^2(-2x-3) = P^2(-3x-3)+2$

So sánh hệ số bậc $2n$ ta có $1+(-2)^n+(-2)^n = (-3)^n$.

Tức là $(-1)^{n+1} = 3^n-2^{n+1}$. Điều này chỉ đúng khi $ n =1$

Vậy $P(x) = ax+b$. Thay vào ta có $a2+b^2 = 1$

câu 4 chia thành 7 hình tháp 3 ô, mỗi hình tháp tổng chẵn nên có 1 số chẵn suy ra đs là 7

em viet nham de anh a , de dung phai la$a, b,c$ la do dai 3 canh tam giac . CMR \sum \frac{a}{b} +3 \geq 2\sum \frac{a+b}{b+c}$

Lời giải của mình, dùng S.S . Giả sử $a$ là số nhỏ nhất

Điều cần chứng minh tương đương với $\sum \frac{a}{b} - 3 \geq 2(\sum \frac{a+b}{b+c}$

Hay $(a-b)^2\frac{c^2+ca+cb-ab}{ab(a+c)(b+c)}+(a-c)(b-c)\frac{c^2+c(b-a)+ab}{ac(a+c)(a+b)}$ ( điều này đúng do $a$ là số nhỏ nhất ). Ta có điều cần chứng minh 

từ đã , e k theo làm toán thì sao :v ai nói trước chi được , e chỉ biết là hiện tại e hơi thích 1 chút thôi chứ sau này biết sao đc
mà sao lại chửi nữa :| chưa gây hấn gì mà ==

từ từ ông ơi :v mỗi người bình tĩnh lại chút nào :|

em không chửi ai cả , lí do e bực mình nó klq đến toán lắm và nó chỉ kéo dài 1 khắc , và phần sau đó thì hoàn toàn chỉ là liên quan đến mình e .
tất nhiên là quan điểm của e khác nhưng e k phủ nhận những gì a nói , e đơn giản là nêu cách nghĩ của mình , tất nhiên là sau này e sẽ nghĩ khác đi , nhưng khác tnao thì lúc đấy mới biết được

em muốn rep anh harrypotter một chút ạ , về khổ cuối cùng ( đoạn đầu thì e không có đủ quyền dể tranh luận ) . em thì đầu óc cũng chỉ như người bình thường , nhưng cũng có chút may mắn được biết 1 ít về toán cao cấp , nói chung cũng là phần nhỏ thôi nhưng cũng nhận thấy nó khác tnao , nên e nghĩ sau này cũng k gặp vấn đề gì lớn lắm , cảm ơn anh ạ

:v

Bài 4 : $f(x+f(y)) = 2y+f(x) \implies f$ song ánh nên tồn tại $a$ để $f(a) = 0$

$P(x,a) \implies a = 0$

$P(0,y) : f(f(y)) = 2y \implies f(x+f(y)) = f(x)+f((y))$. Do $f$ là song ánh nên thay $f(y)$ bở $y$ nên $f(x+y) = f(x)+f(y)$

Mà $f$ liên tục nên $f(x) = ax$. Thay vào có $a = \sqrt{2}$ hoặc $a = -\sqrt{2}$

Bài 6 : Xét tất cả các đường chéo có độ dài trên sẽ lập thành chu kì như sau : $A_1 \rightarrow A_4 \rightarrow A_7 \rightarrow A_{10} \rightarrow...... \rightarrow A_1$, chu kì có độ dài $38$.

Chu kì trên đi qua tất cả các đỉnh đúng 1 lần và chứa tất cả đường chéo cùng độ dài với $A_1A_4$ . Ta cần chứng minh số cạnh đen và số cạnh xanh trong chu kì trên là bằng nhau

Xét trong chu kì trên, ta gọi một đoạn là đoạn đen nếu tất cả các đỉnh trong đoạn đó màu đen, tương tự với đoạn xanh

Thật vậy, nếu đoạn đó chứa $n$ điểm thì sẽ có $n-1$ cạnh. Mà số đoạn đen bằng số đoạn xanh ( hiển nhiên ) , giả sử bằng $k$, khi đó số cạnh đen $=$ số cạnh xanh $= 19-k$. Ta có điều cần chứng minh

Bài 5 :  Áp dụng bổ đề quen thuộc sau : $S(n(10^k-1)) = 9k$ với mọi $n <10^k-1$

Thật vậy, ta có nếu $ 3|n$ thì $S(xn) \equiv xn \equiv 0 $ (mod $3$) nên $S(xn)$ không thể nhận mọi số dư modulo $n$

Nếu $(n,3) = 1$ ; Ta chọn $x = 10^t -1$ với $t > log_{10}(n+1)$ và $9t \equiv k$ (mod $n$). Khi đó $S(n(10^t-1)) = 9t \equiv k $ (mod $n$)

Vậy đáp số là tất cả những số không chia hết cho $3$

Lời giải bài 2 của em ạ : 

1) Ta chứng minh đường thẳng qua $X,Y,Z$ vuông góc $BC,CA,AB$ đồng quy 

Gọi $H$ là trực tâm $\triangle ABC$ , $G$ là cực trực giao của $d$ đối với $\triangle ABC$ . Gọi $K$ là điểm chia $GH$ theo tỉ số $k$ . Khi đó theo định lý thales , $XK,YK,ZK$ vuông góc $BC,CA,AB$ nên đường thẳng qua $X,Y,Z$ vuông góc $BC,CA,AB$ đồng quy 

2) Ta chứng minh bài toán

Gọi $J$ là giao điểm của $(BYK) , (CZK)$ , khi đó ta có $(JB,JC) = (JB,JK) +(JK,JC) = (YB,YK) +(ZK,ZC) = (EB,BH) + (CH,CF) = (BH,CH) = (AB,AC)$ nên $J$ nằm trên $(O)$ 

Suy ra $(AXK) , (BYK) , (CZK)$ đồng quy tại $J$ nằm trên $(O)$

Gọi $V$ là giao điểm của $KJ$ với $(O)$ khác $J$ . Ta có $\angle VAC = \angle KJC = \angle KZF = \angle HCF$ cố định do $d$ cố định và $\triangle ABC$ cố định , suy ra $V$ cố định 

Lời giải bài 1 của em ạ 

Gọi $X$ là giao điểm của $(AMN)$ với $(APQ)$ . $AJ$ cắt $(AMN),(APQ)$ lần lượt tại $H,G$ . $AS$ là đường kính của $(APQ)$ . Khi đó ta có $X,H,S$ thẳng hàng và $\triangle XMN \cap H \sim \triangle XPQ \cap G$ . Ta có biến đổi tỉ số : $\frac{AJ}{AL} = \frac{AH}{AG} = \frac{AH}{AS}.\frac{AS}{AG} = \frac{XH}{XG}.\frac{PQ}{BC} = \frac{MN}{PQ}.\frac{PQ}{BC}$ . Ta có điều cần chứng minh

lời giải của em cho mở rộng bài hình và bài 7 ạ
Bài 7 : 

Xét với $x = y = z = \frac{1}{3}$ thì ta có $c = \frac{9}{10}$

Ta chứng minh hằng số $c= \frac{9}{10}$ thỏa mãn đề bài

Ta có : $|x^3+y^3+z^3 -1| = |x^3+y^3+z^3 - (x+y+z)^3| = |3(x+y)(y+z)(z+x)|$

Và $|x^5+y^5+z^5-1| = |x^5+y^5+z^5-(x+y+z)^5| = |5(x+y)(y+z)(z+x)(x^2+y^2+z^2+xy+yz+zx)|$

Vậy ta cần chứng minh $|x^2+y^2+z^2+xy+yz+zx| \geq \frac{2}{3}$

Có $x^2+y^2+z^2+xy+yz+zx  = (x+y+z)^2-(xy+yz+zx) \geq \frac{2}{3}$ nên ta có điều cần chứng minh

 

Mở rộng bài 6b :