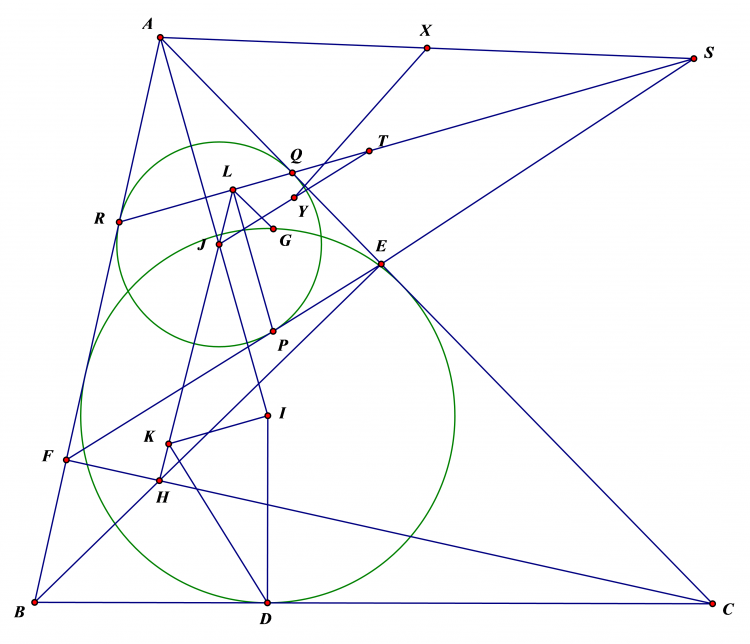
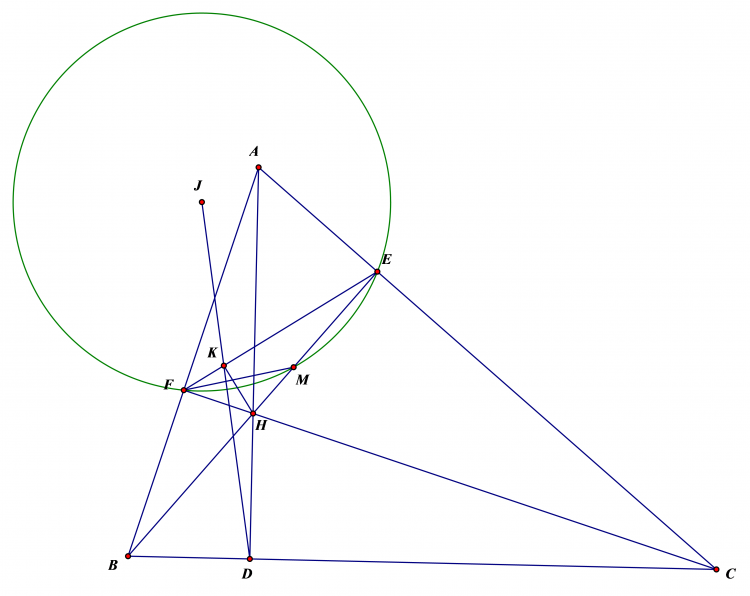
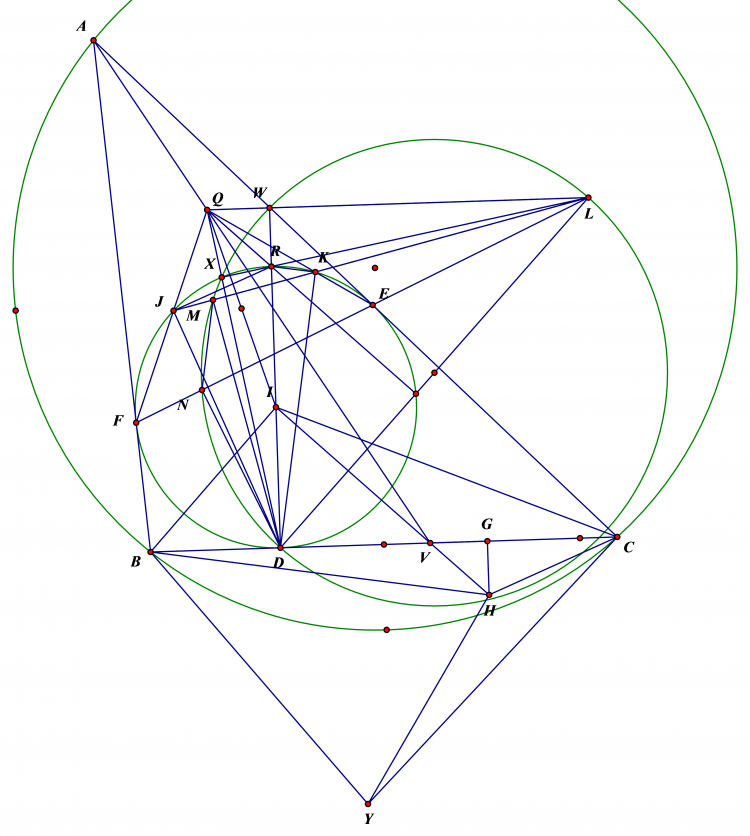
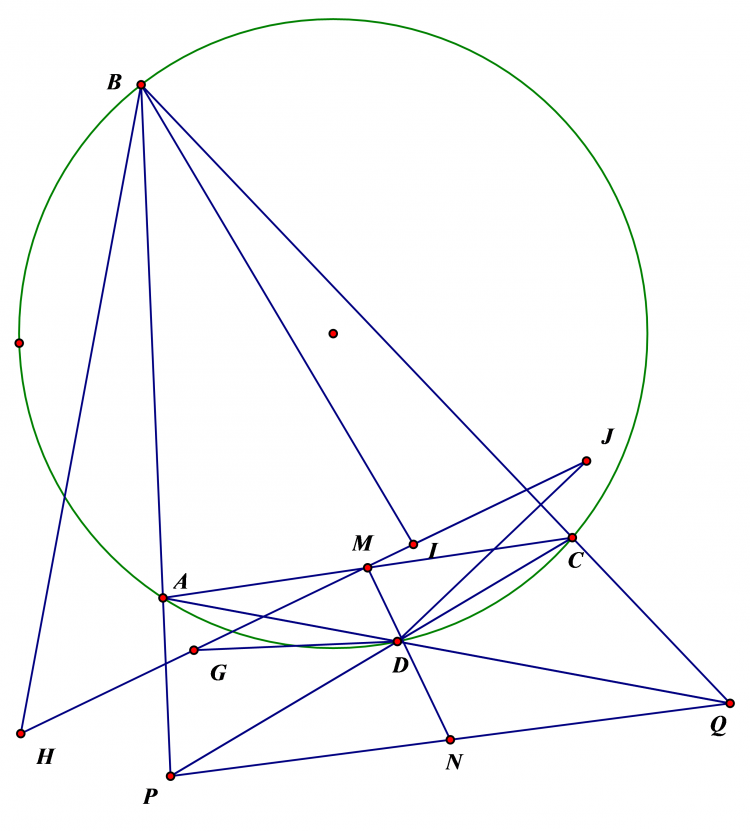
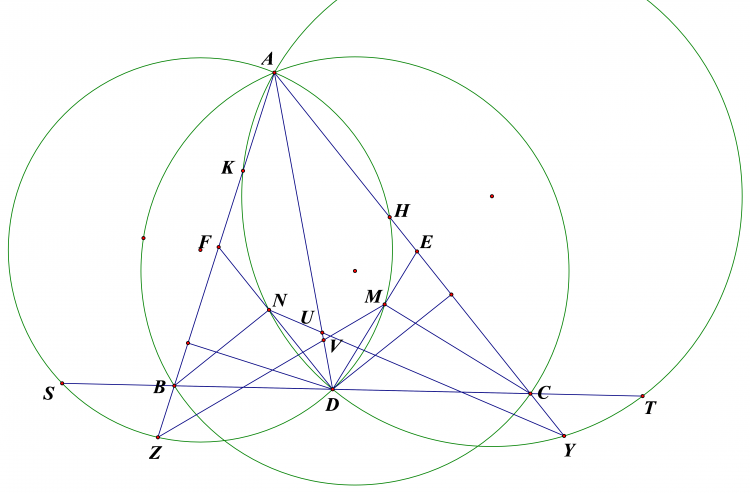
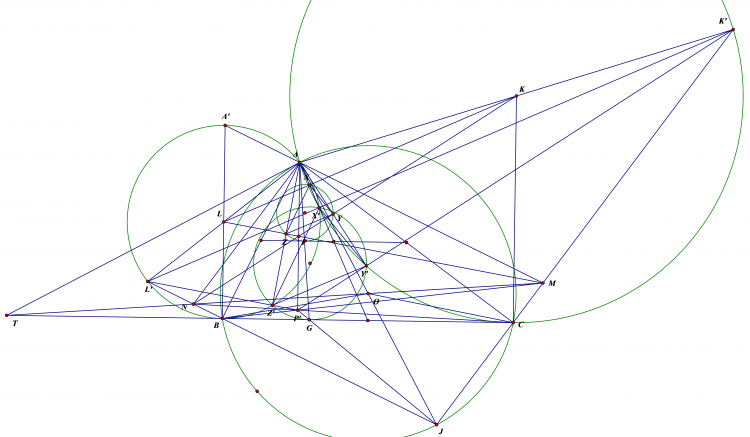
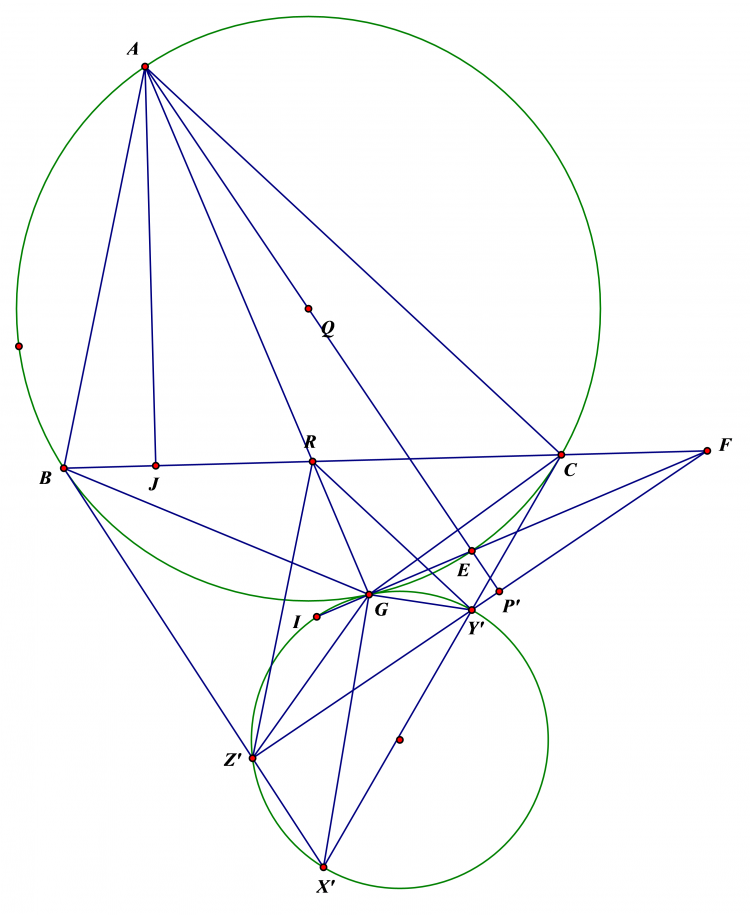
Cho 2 đường tròn ($O_1$) ;($O_2$) bằng nhau ,cắt nhau tại A và B,1 đường thẳng d qua A cắt ($O_1$) ;($O_2$)tại P và Q; 1 đường thẳng khác d qua A cắt ($O_1$) ;($O_2$) tại M và N.  Gọi X và Y là trung điểm MQ và NP .Chứng minh XY luôn đi qua một điểm cố định

 dễ thấy tam giác $BPQ.BMN$ cân  . lấy $E,F$ là trung điểm của $PQ,MN$ ta có $EP=EQ=FP=FQ=QN/2$ nên $XY$ là trung trực của $EF$ . Mặt khác  $EF$ thuộc đường tròn đường kính $AB$ giả sử có tâm là $G$ , suy ra $G$ cũng thuộc trung trực $EF$ và cố định . Tức $XY$ đi qua $G$ cố định.

Bài toán 180. Cho ngũ giác $ABCDE$ lồi, điểm $F$ trên cạnh $AE$ thỏa mãn $\Delta ABC \sim \Delta CDE \sim \Delta BFD.$ Chứng minh $\frac{AF}{FE}=\frac{BF^2}{FD^2}.$

Lời giải bài toán 180. Gọi $DF$ cắt $AC$ tại $G,BF$ cắt $CD$ tại $H,$ có $BCDG,BCDH$ nội tiếp nên $G,B,C,D,H$ cùng thuộc 1 đường tròn.

Theo định lý Pascal thì $BA$ cắt $DE$ tại $I$ thuộc $(GBCDH).$

Do đó $\frac{AF}{FE}=\frac{AB.\sin \widehat{ABF}}{HE.\sin\widehat{FHE}}=\frac{AB.HI}{HE.BC}=\frac{BF^2}{DF^2},$ đpcm.

Bài toán 182. Cho tam giác $ABC$ nhọn, nội tiếp $(O)$ và ngoại tiếp $(I).P$ là điểm bất kì trên cung nhỏ $BC.$

$M,N$ là hai điểm nằm trên cạnh $BC$ sao cho tam giác $MNP$ nhận $(I)$ làm đường tròn bàng tiếp góc $P$ và $(MNP)$ cắt lại $(O)$ ở $X.$

Chứng minh $AX$ đi qua tâm vị tự của $(O),(I).$

Lời giải bài 182 : Đầu tiên ta đi chứng minh $X$ là tiếp điểm của $A-Mix$ với $(O)$

Thật vậy : Gọi $PM,PN$ cắt $(O)$ tại $F,E$ , $EF$ cắt $BC$ tại $Q$ Khi đó $Q$ là điểm $Miquel$ của tứ giác toàn phần $EFMN.PQ$

Ngịch đảo  tâm $X$ phương tích $XM.XE$ hợp đối xứng phân giác góc $MXE$ do $EFMN$ ngoại tiếp nên $XI$ là phân giác góc $QXP$ , (  https://nguyenvanlin...ao-doi-xung.pdf )

có$\widehat{QXB}=\widehat{XBC}-\widehat{XQC}=\widehat{XBC}-\widehat{XFP}=\widehat{PXC}$ nên $XI$ cũng là phân giác góc $CXB$ nên $X$ là tiếp điểm của $A-Mix$ với $(O)$

Xét các tâm vị tự ngoài của $(O),(I),(A-Mix)$ thì theo định lý $Monge$ thì $AX$ đi qua tâm vị tự của $(O),(I).$

Bài toán 176. Cho tam giác $ABC$ nội tiếp $(O),B,C$ cố định, $A$ di chuyển trên cung lớn $BC,$ phân giác $AD,K$ bất kì cố định trên trung trực $BC,$ đường thẳng qua $D$ vuông góc $BC$ cắt $AK$ tại $T.$ Chứng minh $(T,TD)$ luôn tiếp xúc với 1 đường tròn cố định khi $A$ thay đổi.

Bài 171 : ta có $A(ROHM)=-1$ , Gọi $I$ là trung điểm $H$ thì $OI$ vuông góc $AG$ ,$OH$ cắt $AM$ tại $K$ thì $O$ là trung điểm $HK$ , mà $A(ROHM)=-1$ nên $AR$ song song $OH$

Lời giải bài toán 175.

Vị tự tâm $H$ tí số $1/2$ , Gọi $HE,HF$ vuông góc với $AM,AN$ , ta chứng minh $(DEF)$ tiếp xúc với $(Euler)$ của tam giác $ABC$

Trước tiên , $AH$ cắt $BC$ tại $K$ thì$\overline{AH}.\overline{AK}=\overline{AF}.\overline{AD}=\overline{AE}.\overline{AM}$ nên $(DEF)$ đy qua $M$

 Gọi tiếp tuyến tại $A$ cắt $BC$ tại $T$ , theo bài toán quen thuộc thì $E$ thuộc $(A-Apolo)$ Suy ra $TE=TA$ và $ED$ là đối trung của $EBC$ suy ra $ED,EM$ đẳng giác trong  góc $BEC$ nên $\widehat{DEM}=\widehat{BEC}-2\widehat{MEC}=\widehat{B}-\widehat{C}=180^0-\widehat{AOM}$

 Suy ra $\widehat{EDC}=\widehat{AMC}-\widehat{DEM}=90^0-\widehat{MAO}=90^0-\widehat{KAD}=\widehat{ADK}$

Chính vì vậy $ME=MF$ ta có , trung trực của $EF$  vừa đy qua tâm $(Euler)$ của tam giác $ABC$ vừa đy qua tâm $DFE$ và $M$ nên $(DEF)$ tiếp xúc với $(Euler)$ của tam giác $ABC$ tại $M.$

Bài toán 196. Cho tam giác $ABC$ ngoại tiếp $(I)$ có tiếp điểm với $BC$ là $D$ , đường cao $BE,CF$ cắt nhau tại $H$.  Đường tròn nội tiếp tam giác $AEF$ cắt $EF,FA,AE$ tại $P,R,Q$ . Lấy $K$ sao cho $IK \perp IA$ và $DK=DI$ . $HK$ cắt $AI,RQ$ tại $J,L$ . Lấy $G$ đối xứng với $J$ qua $PL$ . $QR$ cắt $EF$ và đường thẳng qua $J$ song song với $EF$ tại $S,T$. $X,Y$ là trung điểm của $AS,JT$.Chứng minh rằng $LG \perp XY$ 

Bài 172 (sáng tác từ một bài toán của bạn Bảo ) : Cho tam giác $ABC$ cố định có đường cao $AH$ , $P$ di chuyển trên tia đối của tia $HC$ , $M$ đối xứng với $C$ qua $H$ . $MN$ song song với $AC$ với $N$ thuộc $AP$ . $Q$ là trung điểm $AH$ . $PQ$ cắt $HN$ tại $D$. Đường tròn $(X)$ thay đổi qua $D$ và tiếp xúc với đường tròn euler của tam giác $AHD$ cắt $DA,DH$ tại $F,E$ . Chứng minh : $(XFE)$ tiếp xúc với đường thẳng cố định khi $P$ và $(X)$ thay đổi

Bài toán 186: Cho tam giác $ABC, $đường cao $AD,BE,CF$ đồng quy tại $H.HK$ vuông góc với $EF.M$ thuộc $BE$ sao cho $KM$ song song với $BC.J$ là tâm $(MEF).$ Chứng minh $J \in DK.$

Lời giải bài 185 :  

Ta sẽ chứng minh  $K$ thuộc đường thẳng qua $B$ vuông góc với $OO'$

Để dễ nhìn, ta viết lại đề như sau : Cho tam giác $ABC$ ngoại tiếp $(I),(I)$ tiếp xúc với $BC,CA,AB$ tại $D,E,F.G$ đối xứng với $D$ qua trung điểm $BC.H$ bất kì sao cho $GH$ vuông góc $BC.$ Đường thẳng qua $D$  vuông góc với $HB,HC$ cắt $(I)$ tại $K,J.JK$ cắt $FE$ tại $L.$ Chứng minh $DL$ vuông góc với $IH.$

Giải : Hạ $DM,DN$ vuông góc với $JK,EF$ , Ta có : $\frac{JM}{KM}=\frac{JM}{MD}.\frac{MD}{MK}=\frac{GH}{BG}.\frac{CG}{HG}=\frac{BG}{CG}=\frac{CD}{BD}=\frac{EN}{FN}$

Gọi $FJ$ cắt $KE$ tại $Q,W$ là điểm $Miquel$ của tứ giác toàn phần $JKEF.LQ$ thì theo tỉ số trên có $(LJF),(LMN),(LEK)$ đồng trục $LW.$

Gọi $DQ$ cắt $(I)$ tại $X,R$ đối xứng với $D$ qua $I.$ Do $\overline{QW}.\overline{QL}=\overline{QJ}.\overline{QF}$ nên $Q$ thuộc trục đẳng phương của $(DMNL)$ nên $X$ thuộc $(MNDL),$ mà $DW$ và $IW$ cùng vuông góc với $QL$ (do $QX.QD=QW.QL$ và góc $DXL$ vuông) nên $DR$ vuông góc với $QL \Rightarrow R$ là trực tâm tam giác $QDL$ nên $QR$ vuông góc với $DL.$

Bây giờ ta sẽ chứng minh $QR$ song song $HI.$ Dựng $Y$ nằm ngoài tam giác $ABC$ sao cho$\widehat{HBY}=\widehat{\frac{B}{2}},\widehat{HCY}=\widehat{\frac{C}{2}}.$

Ta có tam giác $RJK$ đồng dạng với $HBC$ và theo cách dựng $Y$ ta cũng có được tam giác $QJK$ đồng dạng $YBC.$

Mặt khác , xét tam giác $BCH$ có $BY,BI$ đẳng giác góc $B;CY,CI$ đẳng giác góc $C$ nên $Y,I$ liên hợp đẳng giác tam giác $HBC$ nên $HI,HY$ đẳng giác góc $H.$

Chính vì vậy $\widehat{QRK}=\widehat{YHC}=180^0-\widehat{BHI}$ và  $BH,RK$ song song với nhau nên $QR,HI$ song song với nhau.

Kết hợp với $QR$ vuông góc với $DL$ suy ra $DL$ vuông góc với $IH,$ đpcm.

Lời giải bài toán 177.

Bổ đề. Cho tam giác $ABC$ , $D,E$ nằm trên $AB,AC$ , $K,H$ là trực tâm tam giác $ABC,ADE$ , $M,N,P,Q,F$ là trung điểm $BC,CE,DE,BC,DC.$ Khi đó tam giác $AHK$ đồng dạng tam giác $FNM.$

Chứng minh. Gọi $J,I$ là tâm ngoại $ABC,ADE$ , ta có $\frac{AH}{AK}=\frac{IP}{JQ}=\frac{DE}{BC}=\frac{FN}{FM}$

Và dễ dàng chứng minh :$\widehat{HAK}=\widehat{NFM}$ suy ra $AHK$ đồng dạng tam giác $FNM$

Từ đây còn suy ra $\frac{HK}{MN}=\frac{HA}{FN}=\frac{2PI}{PE}=2tan\widehat{DEI}=2cot\widehat{DAE}$

Trở lại bải toán :

Gọi $H,G,I,J$ là trực tâm tam giác $BAQ,PAD,PBC,CDQ$ , ta sẽ chứng minh $GJ=HI$

Thật vậy , gọi $M,N$ là trung điểm $AC,PQ$ , khi đó theo Bổ đề $\frac{GJ}{MN}=2 cot\widehat{ADP}$

 Mặt khác , ta cũng có $\frac{HI}{MN}=2cot\widehat{ABC}$ từ đó suy ra$GJ=HI$

Bài toán 178. Cho tam giác $ABC$ nội tiếp $(O)$ có trực tâm $H,$ phân giác $AD.M$ là điểm chính giữa cung $BHC$ của $(BHC).BM,CM$ cắt $AC,AB$ tại $E,F.EF,AM$ cắt nhau tại $P.K$ là tâm $(AEF).$ Chứng minh :$P$ là trực tâm tam giác $KBC$ và $KA=OD.$ 

Bài toán 184. Cho tam giác $ABC$ , $M$ nằm trên đoạn $BC$ , $K,L$ là tâm ngoại tiếp $(ABM),(ACM).D,E,F,X,Y,Z,T$ lần lượt là trung điểm $MA,MB,MC,KB,KM,LM,LC.YZ$ cắt $XT$ tại $N.NL,NK$ cắt $BC$ tại $P,Q.$ Chứng minh $(DPF)$ tiếp xúc $(DEQ).$

có thống kê rồi các bác ơi........ e đứng thứ 542.. điểm năm nay cao thật

Bạn xem danh sách ở đâu vậy

Thế mấy bác xem 190 thì được cái gì không

Lời giải bài 1 :

Dễ dàng thấy $ANDY,AMDZ$ nội tiếp . Gọi $(AND)$ cắt $BC,BA$ tại $T,K$ . $(ADM)$ cắt $BC,AC$ tại $S,H$

Hạ đường cao $DP,DQ$ xuống $AB,AC$ ta có $EH.EA=EM.ED=EP.EC=>\frac{EA}{EC}=\frac{EP}{EH}=\frac{EA+EP}{EC+EH}=\frac{AP}{HC}$

Tương tự suy ra $\frac{AQ}{KB}=\frac{AF}{FB}=\frac{AE}{EC}=\frac{AP}{HC}$ nên $CH=BK$

Từ đó $\frac{CS}{CH}=\frac{CA}{CD}=\frac{BA}{BD}=\frac{BT}{BK}$ nên $CS=BT$ nên $BS=CT$

Vậy $\frac{BS}{BZ}=\frac{BA}{BD}=\frac{CA}{CD}=\frac{CT}{CY}$ nên $BZ=CY$

Em có ý tưởng khác như sau

$AI$ cắt $(I)$ tại $J,Y$. $DJ$ cắt phân giác ngooài góc $\widehat{BAC}$ tại $X$ . khi đó $(AXYD)$ thuộc đường tròn đường kính $XY$,

mặt khác ,$\widehat{MDY}=\widehat{EJY}=\widehat{MAY}$ và tương tự suy ra $ADMNXY$ cùng thuộc đường tròn đường kính $XY$ . 

Nhận thấy $AY$ là phân giác $\widehat{MAN}$ nên $XY$ là trung trực $MN$ . Nếu cho $XY$ cắt $(I)$ tại $H$ thì $AH,AD$ đẳng giác góc $A$

 Việc còn lại ta chứng minh $AD,AR$ đẳng giác . Thật vậy , Gọi phân giác ngoài tam giác $ABC $ là $AK$ thì $K(AIRD)=-1=>A(KIRD)=-1$ nên $AR,AD$ đẳng giác . suy ra $AR$ đy qua $H$ , Vì vậy $XY,AR$ cắt nhau trên $(I)$

Lời giải bài 1 :

Gọi Phân giác $FHB$ cắt $(HB)$ tại $Y$ ,cắt $AB$ tại $X$

 Ta có $\triangle DFB \sim \triangle DCE$ nên $\triangle DLK \sim \triangle DBE$ nên $\widehat{DKL}=\widehat{DBE}=\widehat{DYH}$ nên $KQ \parallel YH$

Lại có $\frac{DK}{DN}=\frac{DL}{DM}$ nên $KL \parallel MN$

Và $D(AFNB)=D(AEMC)$ nên $EF,BC,MN$ đồng quy  nên $CM,BN,AD$ đồng quy

$KQ$ cắt $AB$ tại $Z$ thì  do $N(MDBM)=-1$ nên $K$ là trung điểm $ZQ$

Khi đó $\frac{XY}{KQ}=\frac{XY}{KZ}=\frac{NY}{NK}=\frac{YK}{KD}$ nên $XK \parallel QD$ nên $X$ trùng $S$ tức là $S$ nằm trên phân giác $FHB$ . tương tự với $T$ suy ra $T,H,S$ thẳng hàng

Lời giải bài 2 :

Giả sử $K,L$ là giao của $BH,CH$ với $EF$ . Ta sẽ chứng minh $K,L$ là trực tâm $MDE,MDF$ và thuộc $(H,HM)$

Thật vậy,$DM$ cắt $EF$ tại $N$ . $AI$ cắt $(O)$ tại $G$

Ta có $\triangle CLE \sim \triangle BKF$ và $\widehat{FBN}=\widehat{ECN}$ ( do $N(CBEN)=-1$ nên $ND$ là phân giác $BNC$ ) suy ra $\frac{NE}{NL}=\frac{NF}{NK}=>\frac{NL}{NK}=\frac{NE}{NF}=\frac{DC}{DB}$

Mà $\triangle GBC \sim \triangle HKL$ và $\widehat{IGB}=\widehat{MHK}$ và $\frac{NK}{NL}=\frac{DB}{DC}$ ,dựng vuông góc từ $D,N$ với $BC,EF$ cắt $GI,HM$ tại $I,H$ nên ta có hình $MKHL \sim IBGC => HK=HM=HL$

Từ đó $K,L$ thuộc $(H,HM)$

Mặt khác $\widehat{KMD}=\widehat{BID}=\widehat{GIC}$ nên $MK \parallel IC \perp ED$ từ đó $K$ là trực tâm $DME$ . tương tự với $L$ ta có dpcm

Lời giải bài 2

Gọi $Y$ là giao 2 tiếp tuyến tại $B,C$. $Z$ là trung điểm $OY$ . $J$ đối xứng với $O$ qua $BC$ . $N,M$ là trung điểm cung $BC,BC$

Ta có : $ON^2=OM.OY=OJ.OZ$ , suy ra $AZ,AJ$ đối xứng nhau quá phân giác góc $A$

Ta sẽ chứng minh $AX$ đi qua $Z$ cố định

Nghịch đảo $N$ tâm $A$ , phương tích $AB.AC$ hợp đối xứng trục phân giác góc $A$

Biến $H,B,C,O,BC \mapsto P,C,B,T,(O)$ . Trong đó $T$ đối xứng với $A$ qua $BC$

Gọi $BT,CP$ cắt $OC,BH$ tại $K,L$  mà $\widehat{OCA}=\widehat{BTA},\widehat{ABH}=\widehat{OPC}$ nên $KACT,ALPB$ vội tiếp

Từ đó $\widehat{KAC}=180-\widehat{BTC}=180-(180-BPC-\widehat{BAC})=180-LAC$

Suy ra $K,A,L$ thẳng hàng 

Áp dụng định lí Dersagues cho 2 tam giác $BHT,CPO$ , khi đó $TO,HP,BC$ đồng quy tại $X'$

Theo tales thì $AX'$ đi qua $J$

Chính vì vậy phép nghịch đảo $N$ :$X' \mapsto X$

Vậy $AX,AJ$ đẳng giác  , nên $AX$ đi qua $Z$ cố định do $AZ,AJ$ đối xứng nhau quá phân giác góc $A$

Lời giải bài 1 :

. Đối trung $AG$của tam giác $ABC$.$MA$ cắt $BL$ tại $A'$ .  $BM$ cắt $CN$ tại $P'$

Ta sẽ chứng minh $AP' \perp  BC$  .Ta có $\widehat{NAB}=\widehat{MAC}$ .và $NBA=MCA=90$  Dựng $U$ nằm ngoài tam giác và $AU \perp BC$ sao cho $\frac{AU}{BC}=\frac{AB}{BN}=\frac{AC}{CM}=>\bigtriangleup NBC\sim \bigtriangleup BAU,\bigtriangleup MBC\sim \bigtriangleup CUA$ Từ đó $BU\perp CN ,CU\perp BM$ nên $P'$ là trực tâm tam giác $UBC$ . Khi đó $AP' \perp BC$.

Gọi $LM$ cắt $AP'$ tại $P_1$.Do $L$ là trung điểm của $A'B$ nên $P_1$ là trung điểm $AP'$. trương tự suy ra $P'=P_1$ và là trung điểm $AP'$

$V_{A}^{2} :K,L,X,Y,Z,P \mapsto  K',L',X',Y',Z',T',P'$ Khi đó $P'$ là giao của $BM,CN$ ta chứng minh $(X'Y'Z')$ tiếp xúc $BC$

Ta sẽ chứng minh $AP' \perp  BC$  .Ta có $\widehat{NAB}=\widehat{MAC}$ .  Dựng $U$ nằm ngoài tam giác và $AU \perp BC$ sao cho $\frac{AU}{BC}=\frac{AB}{BN}=\frac{AC}{CM}=>\bigtriangleup NBC\sim \bigtriangleup BAU,\bigtriangleup MBC\sim \bigtriangleup CUA$ Từ đó $BU\perp CN ,CU\perp BM$ nên $P'$ là trực tâm tam giác $UBC$ . Khi đó $AP' \perp BC$

Tiếp theo ta có : $(AX'Z'BL')(AX'Y'CK')$ tiếp xúc với $BC$,.Mặt khác , Gọi tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$ . Khi đó : $MN$ đy qua $T$ . $AO$ cắt $(O)$ tại $J$ .Khi đó , do $(TGBC)=-1$ nên $J,G,P'$ thẳng hàng

Nghịch đảo tâm $A$ phương tích bất kì : ( tên điểm vẫn giữ nguyên khi nghịch đảo )

Cho tam giác $AB$  nội tiếp $(Q)$ có đường cao $AJ$ . tiếp tuyến tại $B,C$ của $(ABC)$ cắt nhau tại $X'$. trung tuyến đỉnh $A$ cắt $(ABC)$ tại $G$. $(AGJ)$ cắt $AQ$ tại $P'$ . Đường thẳng qua $P'$ vuông góc với $AQ$ cắt $BX',CX'$ tại $Z',Y'$ . Chứng minh :$(X'Z'Y')$ tiếp xúc $(Q)$

Giải : ,

Gọi đường kính $AE$ . $GE$ cắt $BC$ tại $F$ . $R$ là trung điểm $BC$.  

Giả sử : $(BRG)(CRG)$ cắt $BX',CX'$ tại $Z_1,Y_1$ khi đó $\frac{RZ_1}{RY_1}=\frac{GZ_1}{GR}=\frac{GB}{GC}=\frac{AC}{AB}$

Suy ra $\bigtriangleup ABC \sim \bigtriangleup RY_1Z_1 \Rightarrow \widehat{RY_1Z_1}=\widehat{RY_1C}$ nên $R$ là tâm bàng tam giác $X'Y_1Z_1$ . Suy ra $(Q)$ là đường tròn $Mixtilinear$ của tam giác $X'Y_1Z_1$ nên $(X'Y_1Z_1)$ tiếp xúc $(Q)$

Ta cần chứng minh $Y_1,Z_1\equiv Y',Z'$ . Gọi $I$ là trung điểm cung $Y_1Z_1$ của $(X'Y_1Z_1)$  , khi đó Ta có các tc sau của dường tròn $Mixtilinear$ được cm ở đây ( https://nguyenvanlin...mixtilinear.pdf )

1) $IG\perp GR$

2) $IG,BC,Y_1Z_1$ đồng quy

 Khi đó $Y_1Z_1$ đy qua $P'$ và $Y_1Z_1$ vuông góc $AQ$( cộng góc ) nên $Y_1,Z_1\equiv Y',Z'$ . Ta có dpcm

Lời giải bài 2 :

Đầu tiên Ta có $\widehat{BFP}=\widehat{CEP}=\widehat{BAC}$ nên $FOPB,EOPC$ nội tiếp , Gọi $K,L$ là tâm $(OPB),(OPC)$ , Ta có $(K)=(L)$ . Dựng $X$ sao cho $X$ thuộc $PO$ và $\widehat{XKO}=\widehat{BAC}$ Nên $X$ cố định.  Mặt khác $\widehat{FPE}= \widehat{BAC}$ nên ta có :$\widehat{FKX}=\widehat{ELX}$ Do đó2 tam giác $FKX,ELX$ bằng nhau nên $XE=XF$ suy ra trung trực $FE$ đy qua $X$ cố định