Vấn đề mở rộng định lý Feuerbach–Luchterhand
Vấn đề được nêu trong file đính kèm
June-14-2014-Feuerbach-Luchterhand.pdf 106.14K
544 Số lần tải
Oai Thanh Dao nội dung
Có 57 mục bởi Oai Thanh Dao (Tìm giới hạn từ 29-04-2020)
#567330 Định lý Đào
Đã gửi bởi
on 21-06-2015 - 20:12
trong
Tài liệu, chuyên đề, phương pháp về Hình học
#567695 Định lý Đào
Đã gửi bởi
on 23-06-2015 - 17:45
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Cách xác định $A_1$ còn mờ ám. Vì có hai vị trí $A_1$ (vị trí còn lại nằm ở cung đối diện). Tương tự với $B_1,C_1,...$
Thực ra anh cũng nhận ra điều đó(nhưng lười viết), cảm ơn em nhé. Anh bổ sung như sau:
Nếu đường tròn $A_1$ như hình vẽ thì tất cả các đường tròn Thebault tương ứng với $B_1,C_1,...,F_1$ còn lại như hình vẽ.
Nếu đường tròn tương ứng với $A_1$ phía đối diện thì tất cả các đường trờn tương ứng với $B_1,C_1,...,F_1$ cũng nằm ở phía đối diện
Nếu đường tròn tương ứng với $A_1$ nằm ngoài thì tất cả các đường tròn tương ứng $B_1,C_1,...,F_1$ cũng năm phía ngoài.(nằm ngoài cũng có hai trường hợp)
#567895 Định lý Đào
Đã gửi bởi
on 24-06-2015 - 18:07
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Lời giải cho vấn đề tám đường tròn, Proposed by Đào Thanh Oai, solution by Luis Gonzalez
File gửi kèm
-
Tam duong tron.pdf 251.5K
521 Số lần tải
#579830 Định lý Đào
Đã gửi bởi
on 08-08-2015 - 20:59
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Mở rộng định lý Sondat:
Cho tam giác $ABC$, cho $P$ là một điểm bất kỳ trên mặt phẳng, cho đường thẳng $d$ cắt ba cạnh tam giác tại $A_0$, $B_0$, $C_0$ ba đường thẳng tương ứng qua $A_0,B_0,C_0$ và song song với $AP, BP, CP$ tạo thành tam giác $A_1,B_1,C_1$. Theo định lý Maxwell thì ba đường thẳng qua $A_1, B_1, C_1$ và song song với $BC,CA,AB$ một cách tương ứng lại sẽ đồng quy tại một điểm ta gọi điểm này là $P_1$. Khi đó đường thẳng $d$ chi đôi đoạn thẳng $PP_1$. Trong trường hợp $P$ là trực tâm vấn đề này là định lý Sondat.
#574934 Định lý Đào
Đã gửi bởi
on 24-07-2015 - 09:34
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Mở rộng định lý đường thẳng Steiner và đường tròn Miquel
Cho $ABC$ là một tam giác, Cho $P_1$ là một điểm bất kỳ trong mặt phẳng. Cho $L$ là đường thẳng cắt $BC, CA, AB$ tương ứng tại $A_0,B_0,C_0$. Định nghĩa $A_1$ là một điểm trên mặt phẳng sao cho $B_0A_1$ song song $CP_1$, $C_0A_1$ song song với $BP$. Định nghĩa $B_1, C_1$ tương tự.
Cho $ABC$ là một tam giác, Cho $P_1$ là một điểm bất kỳ trong mặt phẳng. Cho $L$ là đường thẳng cắt $BC, CA, AB$ tương ứng tại $A_0,B_0,C_0$. Định nghĩa $A_1$ là một điểm trên mặt phẳng sao cho $B_0A_1$ song song $CP_1$, $C_0A_1$ song song với $BP$. Định nghĩa $B_1, C_1$ tương tự.
1. (Mở rộng đường thẳng Steiner) Hãy chỉ ra $A_1, B_1, C_1, P_1$ thẳng hàng.
2. (Mở rộng đường tròn Miquel). Định nghĩa $A_2,B_2,C_2,P_2$ là điểm liên hợp đẳng giác của $A_1,B_1,C_1,P_1$ lần lượt tương ứng với các tam giác $AB_0C_0, BC_0A_0, CA_0B_0$ và $ABC$ (respectively). Hãy chỉ ra $A_2,B_2,C_2,P_2$ nằm trên đường tròn.
#550909 Định lý Fermat đã được chứng minh một cách ngắn gọn?
Đã gửi bởi
on 02-04-2015 - 14:46
trong
Lịch sử toán học
Thấy có bài báo này trên trang web của trường đại học Princeton, mọi người cho ý kiến nhé
http://www.princeton.edu/~aloo/fermat
File gửi kèm
-
fermat.pdf 135.12K
855 Số lần tải
#689997 Tìm các cách chứng minh cho mở rộng định lý Brahmagupta
Đã gửi bởi
on 09-08-2017 - 17:08
trong
Hình học
Trong hình đính kèm. 
Nếu $\frac{MQ}{BA}=\frac{NP}{BC}$ và $\angle MBA = \angle CBN=\frac{\pi}{2}$
Nếu $\frac{MQ}{BA}=\frac{NP}{BC}$ và $\angle MBA = \angle CBN=\frac{\pi}{2}$
Trong đó $D, E$ lần lượt là trung điểm của $MN, PQ$, hãy chỉ ra rằng: $DE \perp AC$
Nếu như $P=Q=B$ thì kết quả này là mở rộng định lý Brahmagupta.
Nếu $P=Q=B$ và $M, B, C$ thẳng hàng và $N, B, A$ thẳng hàng thì đây chính là:
#645114 Tuần 2 tháng 6/2016: Bài toán đường tròn tiếp xúc trên cấu hình về hình vuông
Đã gửi bởi
on 16-07-2016 - 01:43
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Hôm qua mình có trao đổi với một cậu nước ngoại tại đây:
https://groups.yahoo...s/messages/3329
Cậu ấy viết:
Dear friends,
Consider a triangle ABC. Let I be the incenter of ABC. Draw CI such that meet the circumcircle of ABC at C’. Similarly, construct the point B’. Now, draw a line paralell to B’C’ passing throu I, such that intersect AB in I_c and AC in I_b. The lines B’I_b, C’I_c intersect at a point, E, on the circumcircle of ABC. Then, the circumcircle of triangle I_bI_cE is a mixtilinear incircle. See image attached.
I want to know whether this construction is new or not. Thanks in advance.
Best regards,
Emmanuel.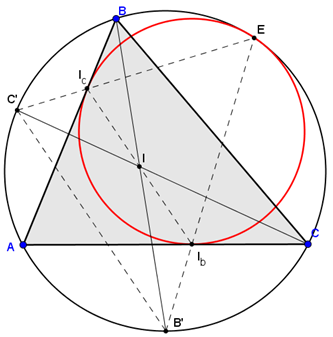
Và tìm ra một mở rộng tại đây: https://groups.yahoo...s/messages/3330
Dear Emmanuel José García, Dear Geometers,
I inspired from your construct. I posed a generalization of Mixtilinear circle as follows:
Let ABC be a triangle, P be a point on the plane, let A'B'C' be the circumcevian of P. Let a line through P and parallel to B'C', the line meets AC, AB at Ab, Ac respectively. Then B'Ab meets C'Ac at a point A'', and circle (AbAcA'') tangent with the circumcircle at A''. Define Bc, Ba, Ca, Cb cyclically , and Define B'', C'' cyclically. Then show that:
1. AA'', BB'', CC'' are concurrent.
2. Six points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic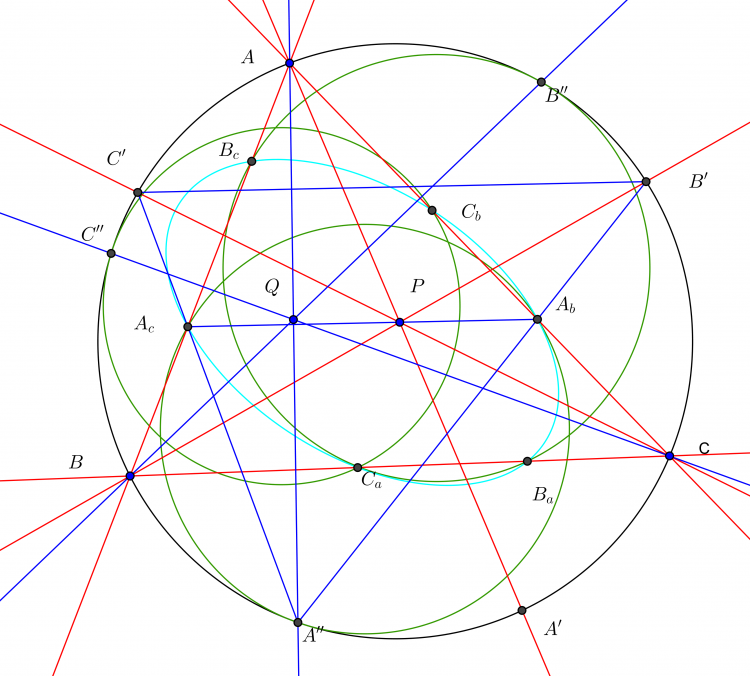
Best regards
Sincerely
Dao Thanh Oai
Tuy nhiên kết quả trên về bản chất sẽ trùng với ý tưởng của Bảo. Mình đã xác nhận tại diễn đàn đó là tuy lấy cảm hứng từ bài của Emmanuel để đưa ra mở rộng của đường tròn Mixtilinear. Nhưng kết quả này được tổng quát hóa trước đó bởi Bảo. Về mặt khoa học như thế coi như đã xác nhận kết quả này không phải của mình mà là của Bảo.
#711477 Sao khóa bài Bất đẳng thức kinh điển mới
Đã gửi bởi
on 24-06-2018 - 02:31
trong
Xử lí vi phạm - Tranh chấp - Khiếu nại
Các bạn cho mình hỏi, sao ai đó khóa bài này của mình?
https://diendantoanh...-kinh-điển-mới/
Bài đó đã được đăng trên diễn đàn toán học cao cấp và đã có nhưng chứng minh và ủng hộ của các nhà toán học mình không hiểu tại sao lại khóa bài?
#686792 Một giả thuyết về phương trình nghiệm nguyên
Đã gửi bởi
on 07-07-2017 - 15:24
trong
Toán học hiện đại
Cho ba số nguyên $A, B, C$ trong đó $A^2+B^2+C^2 \ne 0$; và cho trước một phương trình nghiệm nguyên bất kỳ $f(x,y,z)=0$. Khi đó tồn tại một số $N_0 > 2$ để với $m, n, k \ge N_0$ thì phương trình sau: $f(x,y,z)+Ax^n+By^m+Cz^k=0$ với điều kiện $gcd(x,y)=gcd(y,z)=gcd(z,x)=1$ sẽ có số nghiệm hữu hạn.
Let $A, B, C$ be given three integer numbers, $A^2+B^2+C^2 \ne 0$; and $f(x,y,z)=0$ be given diophantine equation. Then exist $N_0 > 2$ such that $m, n, k \ge N_0$ the equation as follows: $f(x,y,z)+Ax^n+By^m+Cz^k=0$ with condition $gcd(x,y)=gcd(y,z)=gcd(z,x)=1$ has only finitely solutions
#556593 Một giả thuyết về bất đẳng thức trong không gian m chiều
Đã gửi bởi
on 27-04-2015 - 17:09
trong
Đại số tuyến tính, Hình học giải tích
Với không gian hai chiều $f(n,m)=\frac{n}{m}=\frac{n}{2}$
#556536 Một giả thuyết về bất đẳng thức trong không gian m chiều
Đã gửi bởi
on 27-04-2015 - 08:27
trong
Đại số tuyến tính, Hình học giải tích
Cho $X_1,X_2,X_3,.....,X_n$ là $n$ điểm trên mặt cầu trong không gian Euclid m chiều. Khi đó chúng tôi đưa ra giả thiết sau:
$$\prod_{i,j}^{C_n^2}||X_i-X_j|| \leq n^{f(n,m)} ||r||^{C_n^2}$$
Trong đó: $r$ là bán kính mặt cầu
Dấu bằng xảy ra khi các điểm $X_1,X_2,X_3....,X_n$ thỏa mãn điều kiện gì sẽ được chúng tôi làm rõ?
Biểu thức quan hệ $f(n,m)$ sẽ được chúng tôi làm rõ?
Tác giả: Đào Thanh Oai và Quang Dương
Giả thuyết trên được chúng tôi phát triển từ bất đẳng thức quen thuộc trong hình học tam giác:
$\sin A.\sin B. \sin C \leq 3.\sqrt{3}/8$
#711287 Một giả thuyết mạnh hơn định lý lớn Fermat
Đã gửi bởi
on 20-06-2018 - 11:37
trong
Toán học hiện đại
Dựa trên sự quan sát các kết quả liên quan đến định lý Fermat, giả thuyết Beal, giả thuyết ABC....tôi đề xuất một giả thuyết sau đây:
Cho $A, B, C$ là ba số nguyên dương sao cho $A+B=C$ với $(A,B)= (B,C) = (C,A) = 1$. Phân tích ba số $A, B, C$ ra thừa số nguyên tố:
$A=a_1^{x_1}a_2^{x_2}...a_n^{x_n}$,
$B=b_1^{y_1}b_2^{y_2}...b_m^{y_m}$,
$C=c_1^{z_1}c_2^{z_2}...c_k^{z_k}$
Giả thuyết khẳng định khi đó $\min\{x_i, y_j, z_h \} \le 5$ với mọi $1 \le i \le n, 1\ \le j \le m, 1\le h \le k$
Giả thuyết trên nếu được chứng minh nó sẽ rất mạnh, lúc đó các định lý Fermat, giả thuyết Beal, giả thuyết Fermat-Catalan chỉ là các trường hợp đặc biệt. Hiện tại chưa tìm được phản ví dụ.
Đào Thanh Oai
#689274 Một giả thuyết khác về tổng $A+B=C$
Đã gửi bởi
on 02-08-2017 - 11:58
trong
Toán học hiện đại
Cảm nhận riêng của mình là câu hỏi cái này quá khó để biết đúng hay sai. Nếu nó đúng thì chẳng hạn, rõ ràng sẽ giảm việc chứng minh định lý Fermat về hữu hạn trường hợp và chứng minh phương trình $1+a^n=b^n$ vô nghiệm với $n>2$, nhưng việc chứng minh định lý Fermat đã rất rất khó rồi.
Mình nghĩ công việc do hạn chế tầm hiểu biết có ích hơn là cố gắng bác bỏ nó cho $N_0$ nào đó đủ nhỏ.
Cảm ơn bạn đã quan tâm, vì máy tính của mình có chạy đến hết một năm cũng chưa chắc kiểm chứng được với $A, B \le 4*10^18$ nên đành nêu ý tưởng vậy thôi chứ cũng chẳng chứng minh, hay kiểm chứng được. Nhưng có một nhà toán học dự định nó sẽ đúng nếu $N_0=4$ nhưng nó yếu hơn giả thuyết $abc$.
#686376 Một giả thuyết khác về tổng $A+B=C$
Đã gửi bởi
on 03-07-2017 - 18:41
trong
Toán học hiện đại
Giả thuyết sau đây có thể sai, nhưng nếu đúng sẽ rất khó chứng minh, nếu đúng nó là kết quả mạnh hơn của nhiều giả thuyết kết quả nổi tiếng như định lý Fermat, giả thuyết Beal, giả thuyết Fermat Catalan:
Cho $A, B, C $ be là ba số nguyên tố cùng nhau, $gcd(A, B, C)=1$. Theo Định lý cơ bản của số học ta viết:
$A=a_1^{x_1}a_2^{x_2}...a_n^{x_n}$,
$B=b_1^{y_1}b_2^{y_2}...b_m^{y_m}$,
$C=c_1^{z_1}c_2^{z_2}...c_k^{z_k}$
Đặt $N=min\{x_i, y_j, z_h\}$ trong đó $1 \le i le n, 1 \le j le m, 1 \le h le k $
Với một số $N_0 > 3$ sẽ tồn tại một số hữu hạn các số $(A, B, C)$ sao cho $A+B=C$ đồng thời $N \ge N_0$
English version:
Let $A, B, C $ be three positive integer numbers, such that $gcd(A, B, C)=1$
By Fundamental theorem of arithmetic we write:
$A=a_1^{x_1}a_2^{x_2}...a_n^{x_n}$,
$B=b_1^{y_1}b_2^{y_2}...b_m^{y_m}$,
$C=c_1^{z_1}c_2^{z_2}...c_k^{z_k}$
For a positive integer $N_0 > 3$, there exist only finitely many triples $(A, B, C)$ of coprime positive integers, with $A+B=C$, such that: $N \ge N_0$
#688574 Một giả thuyết khác về tổng $A+B=C$
Đã gửi bởi
on 24-07-2017 - 22:22
trong
Toán học hiện đại
Mình xin được viết lại ý của tác giả, vì mình không hiểu được cho đến khi đọc lại 3 lần nên có thể cmt này sẽ có ích với người khác.
Với mọi $N \in \mathbb{Z}_{\geq 4}$, chỉ có hữu hạn bộ 3 số nguyên dương $A,B,C$ thỏa mãn:
1. $A+B=C,$
2. $(A,B,C)=1,$
3. $l(A,B,C) \geq N.$
Ở đây, $l(A,B,C)=\min \left\{ord_{p}(ABC)| p \in Spec(\mathbb{Z}), p | ABC \right\}$.
Có chỗ mình không hiểu trong phiên bản tiếng Việt là câu "tồn tại một số hữu hạn các số", hi vọng tác giả có thể nói rõ ý của mình.
P/S: Nếu cách diễn giải của mình đúng, số $N$ trong giả thuyết là không cần thiết vì nếu giả thuyết đúng cho $N$ thì nó đúng cho mọi $M \geq N$. Như vậy, phát biểu chỉ nên là
Chỉ có hữu hạn bộ 3 số nguyên dương $A,B,C$ thỏa mãn:
1. $A+B=C,$
2. $(A,B,C)=1,$
3. $l(A,B,C) \geq 4.$
Ở đây, $l(A,B,C)=\min \left\{ord_{p}(ABC)| p \in Spec(\mathbb{Z}), p | ABC \right\}$.
Cảm ơn bạn, dùng ký hiệu mình không thạo nhưng mình có thể phát biểu bằng lời ý tưởng của mình nhé:
Nếu ba số nguyên dương $(A, B, A+B)$ nguyên tố cùng nhau thì trong phân tích ra thừa số nguyên tố của ba số $A, B, A+B$ phải có một thừa số với số mũ nhỏ hơn $N_0$, trong đó $N_0$ là một giá trị khá nhỏ $4, 5, 6....$.
PS: Phát biểu như này thì mình không lăn tăn gì cả
#647589 Mở rộng bất đẳng thức Karamata
Đã gửi bởi
on 02-08-2016 - 08:17
trong
Giải tích
Cho $f(x)$ là hàm số thực lồi và liên tục trên $I$. Giả sử $x_1, . . . , x_n$ và $y_1, . . . , y_n$ thuộc $I$ sao cho hai điều kiện sau đây được thỏa mãn:
1. $x_1 \ge x_2 \ge x_3.....\ge x_n,$ và $y_1 \ge y_2 \ge y_3.....\ge y_n$
2. $x_1+...+x_i \ge y_1+.....+y_i$ và $x_{i+1}+...+x_n \le y_{i+1}+...+y_n$ với $i=1,....,n-1$ chứng minh rằng
$$\frac{f(x_1)+f(x_2)+....+f(x_n)}{n}-f(\frac{x_1+x_2+....+x_n}{n}) \ge \frac{f(y_1)+f(y_2)+....+f(y_n)}{n}-f(\frac{y_1+y_2+....+y_n}{n}) $$
Đẳng thức xảy ra nếu và chỉ nếu $x_i=y_i$ với mọi $i \in {1, 2,...,n}$
#711160 Một bất đẳng thức giống bất đẳng thức Muirhead
Đã gửi bởi
on 18-06-2018 - 09:56
trong
Bất đẳng thức và cực trị
Cho $n$ là một số tự nhiên $n \ge 2$ và $x_1, \cdots, x_n$ and $y_1,\cdots, y_n$ là hai bộ số sao cho $(x_1,\cdots, x_n)$ trội hơn bộ số $(y_1,\cdots, y_n)$; Cho $0 \leq a_1, a_2,\cdots,a_n \leq 1$ khi đó ta có:
$$\sum_{\text{sym}} {x_1}^{a_1}{x_2}^{a_2}\cdots {x_n}^{a_n}\leq \sum_{\text{sym}} {y_1}^{a_1}{y_2}^{a_2}\cdots {y_n}^{a_n}$$
Chú ý rằng: Bất đẳng thức trên không phải bất đẳng thức Muirhead
Example: Let $0 \leq a_i \leq 1$ then
1. $4^{a_1}1^{a_2}+ 4^{a_2}1^{a_1} \le 3^{a_1}2^{a_2}+ 3^{a_2}2^{a_1}$
2. $5^{a_1}5^{a_2}2^{a_3}+5^{a_1}5^{a_3}2^{a_2}+5^{a_2}5^{a_1}2^{a_3}+5^{a_2}5^{a_3}2^{a_1}+5^{a_3}5^{a_1}2^{a_2}+5^{a_3}5^{a_2}2^{a_1}
\leq 4.5^{a_1}4^{a_2}3.5^{a_3}+4.5^{a_1}4^{a_3}3.5^{a_2}+4.5^{a_2}4^{a_1}3.5^{a_3}+4.5^{a_2}4^{a_3}3.5^{a_1}+4.5^{a_3}4^{a_1}3.5^{a_2}+4.5^{a_3}4^{a_2}3.5^{a_1}$
Xem thêm:
#704124 Hơn 40 tam giác đều họ tam giác đều mới được phát hiện
Đã gửi bởi
on 23-03-2018 - 09:50
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Tam giác đều Morley, tam giác đều Napoleon luôn là chủ đề nổi tiếng và hấp dẫn đối với những ai đam mê đến hình học phẳng. Tại chủ đề này tôi giới thiệu các bạn hơn 40 tam giác đều mới được chính tôi phát hiện. Các bạn có thể tham khảo tại link sau đây để tham khảo các kết quả này. Có rất nhiều vấn đề cần khám phá xoay quanh hơn 40 tam giác đều và họ tam giác đều này. Đây chắc chắn là những chủ đề thú vị đối vớ những ai có quan tâm đến hình học phẳng. Tôi xin trân trọng giới thiệu cùng các thầy cô và các em học sinh.
- 10 Tam giác đều thứ nhất bạn có thể xem tại đường link sau đây:
http://faculty.evans...cedInETC.html#F
- 10 tam giác đều tiếp theo bạn có thể xem tại link sau đây
https://drive.google...XnKLyw9VIl6zOhh
- Hơn hai mươi kết quả khác tôi sẽ gửi lên sau.
Đào Thanh Oai
#704558 Hơn 40 tam giác đều họ tam giác đều mới được phát hiện
Đã gửi bởi
on 30-03-2018 - 20:51
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Let $ABC$ be a triangle, let $A'B'C'$ be the Morley triangles (First Morely triangle, Second Morley triangle, or third Morley trianhle). Let $B_a$, $C_a$ on $BC$ such that $ A'B_aC_a$ be an equilateral triangle define $C_b$, $A_b$, $A_c$, $B_c$ cyclically. Let $A''$, $B''$, $C''$ be the midpoints of $A_bA_c$, $B_cB_a$, $C_aC_b$ respectively. Then triangle $A''B''C''$ is equilateral triangle and perspective to $ABC$. $A''B''C''$ homothetic to the Morley triangle.
Cho tam giác $ABC$ và $A'B'C'$ là tam giác Morley (tam giác Morley thứ nhất, thứ hai, hoặc thứ ba). Cho các điểm $B_a$, $C_a$ trên $BC$ sao cho $A'B_aC_a$ là tam giác đều. Định nghĩa $C_b$, $A_b$, $A_c$, $B_c$ tương tự. Gọi $A''$, $B''$, $C''$ gọi là trung điểm của $A_bA_c$, $B_cB_a$, $C_aC_b$ khi đó $A''B"C''$ là vị tự của tam giác Morley và thấu xạ với tam giác $ABC$.
#578077 Giả thuyết về sự tăng bậc dẫn đến mất nghiệm của phương trình nghiệm nguyên
Đã gửi bởi
on 03-08-2015 - 10:15
trong
Toán học hiện đại
Giả thuyết của anh không đúng, thử với $95800^4+217519^4+414560^4=422481^4$ (R. Frye 1988).
Thực ra, năm 1967, L. J. Lander, T. R. Parkin, and John Selfridge đã đưa ra một giả thuyết, mở rộng cho định lý Fermat lớn:
Nếu $k>3$ và $\sum_{i=1}^{n}a_i^k= \sum_{i=1}^mb_j^k$ trong đó $a_i \ne b_j$ với mọi thì $1 \le i \le n, 1 \le j \le m$ có nghiệm nguyên dương thì $m+n \ge k$.
Anh có thể xem thêm tại Euler's sum of powers conjecture.
Giả thuyết của anh chắc có thể đúng nếu chỉnh điều kiện từ $k \ge m+n$ thành $k>m+n$.
Cảm ơn em. Giáo sư Đào Hải Long cũng cho anh biết thông tin trên, và đưa đường link :
#577540 Giả thuyết về sự tăng bậc dẫn đến mất nghiệm của phương trình nghiệm nguyên
Đã gửi bởi
on 01-08-2015 - 19:20
trong
Toán học hiện đại
1. Quan sát:
Cho hai hàm số liên tục $f(x)$ và $g(x)$ với $x \in [a,b]$, khi đó khả năng tồn tại một giá trị $x_0$ thực để $f(x_0)=g(x_0)$ là cao hơn so với khả năng tồn tại giá trị nguyên $y_0$ để $f(y_0)=g(y_0)$. Điều này dễ dàng hình dung qua đồ thị về giao điểm của hai hàm số liên tục và giao điểm của hai hàm số rời rạc. Đối với một đa thức khi bậc của đa thức cao lên thì độ rời rạc của đa thức $f(x)$ ($x$ nguyên) càng cao và dẫn đến giá trị $f(x)+f(y)=f(z)$ với $x,y,z$ nguyên càng trở lên khó khăn. Theo chiều hướng đó khi bậc của đa thức $k$ tăng đến một mức độ nào đó thì sẽ dẫn đến phương trình $f(x)+f(y)=f(z)$ hoàn toàn trở lên vô nghiệm. Xuất phát từ nguyên lý đó tôi đưa ra một giả thuyết như sau(chú ý giả thuyết sau chỉ là một cách để cố gắng thể hiện kết quả trong quan sát trên):
2. Giả thuyết: Cho $a$ là một số nguyên khác $0$, $m,n$ là hai số nguyên dương khác nhau, $g(x)$ là một đa thức bất kỳ cho trước, đặt $f(x)=g(x)+ax^k$, khi đó tồn tại một hằng số nguyên dương $k_0$ để với mọi $k \geq k_0$ thì phương trình:
$$f(x_1)+f(x_2)+....+f(x_n)=f(y_1)+....+f(y_m)$$
không có nghiệm nguyên dương khác một.
Chú ý: Tôi thêm chữ khác 1 vào để loại bỏ trường hợp tầm thường cho phù hợp với ý tưởng xuất phát là độ rời rạc của đa thức tăng lên khi bậc của đa thức tăng lên vì với x=1 thì f(1) không thay đổi khi ta chỉ thay đổi bậc của đa thức. Ngoài ra phản biện tại #2 của Zaraki là cho phiên bản version 1
File gửi kèm
-
Version 1.pdf 119K
168 Số lần tải
-
Final version_A conjecture related with the Fermat last theorem.pdf 107.8K
193 Số lần tải
-
Two conjectures in number theory.pdf 127.49K
160 Số lần tải
#578654 Giả thuyết về sự tăng bậc dẫn đến mất nghiệm của phương trình nghiệm nguyên
Đã gửi bởi
on 04-08-2015 - 22:50
trong
Toán học hiện đại
Phiên bản cuối cùng của giả thuyết
File gửi kèm
-
Final version_A conjecture related with the Fermat last theorem.pdf 107.8K
235 Số lần tải
#697380 Chứng minh tồn tại một đường tròn tiếp xúc với hai đường tròn $(ABC)...
Đã gửi bởi
on 28-11-2017 - 20:04
trong
Hình học
Xét phép nghịch đảo tâm $A$ phương tích bất kì, ta chuyển bài toán đã cho về bài toán phụ:
Bài toán phụ. Cho tam giác $ABC,A_1$ là điểm bất kì $,B_1$ là điểm bất kì trên $BA_1,(BCB_1)$ cắt $A_1C$ ở $C_1.$
Chứng minh tiếp tuyến tại $A_1$ của $(AB_1C_1)$ song song với $BC.$
Bài toán phụ được chứng minh bằng cách gọi $A_1x$ là tiếp tuyến $(AB_1C_1)$ và có biến đổi góc
$\widehat{xA_1C_1}= \widehat{A_1B_1C_1}= \widehat{A_1CB}$ suy ra đpcm.
Nhờ bạn vẽ hình lại cho mình được không? Bài toán phụ mình vẽ hình không thấy đúng. Cảm ơn bạn
#697151 Chứng minh tồn tại một đường tròn tiếp xúc với hai đường tròn $(ABC)...
Đã gửi bởi
on 24-11-2017 - 22:29
trong
Hình học
Bài toán: Cho ba đường tròn, đường tròn thứ nhất đi qua bốn điểm $B, C, B_1, C_1$, đường tròn thứ hai đi qua bốn điểm $C, A, C_1, A_1$, đường tròn thứ ba đi qua bốn điểm $A, B, A_1, B_1$. Chứng minh tồn tại một đường tròn tiếp xúc với hai đường tròn $(ABC)$, $(A_1B_1C_1)$ tại hai điểm $A, A_1$
