Với yêu cầu ngày càng cao của VMF, mình giờ đây xin được lập topic "Hội những người độc thân thích chém gió" , để anh chị em đang cô đơn có cơ hội được giao lưu, học hỏi nhau.
Ai đang độc thân thì vào đây nhé !
Điểm danh phát

• L Lawliet[Hội truởng] .
• Tham Lang[Quản lí ][ Vĩnh Viễn ]
• |M|ua |kau v0ng
• BlackSekena
• duongld
• ducthinh26032011
• maikhaiok
• 2Xluxubuhl
• C a c t u s
• nguyenhang28091996(forever)
• minhdat881439
• nthoangcute đề nghị mọi người xử ku này cho anh phát
• ElenaIP97
• WWW
• tieulyly1995
• Celia
• minhtuyb
• hoangtrong2305$\to$ đang có dấu hiệu khả nghi, đề nghị anh em cập nhật thông tin
• le_hoang1995
• NGOCTIEN_A1_DQH
• Kẻ huỷ diệt tranghieu95
• perfectstrong [ Thành viên đuợc đặc cách ]
• namheo1996
• yeutoan11
• Ispectorgadget
• anh qua
• MIM
• Nguyen Duc Nghia
• BoFaKe
• bugatti
• Stranger441
• loyee
• chagtraife
• no matter what
• tramyvodoi
• NGUYEN MINH HIEU TKVN
• Primary
• diepviennhi
• Dung Dang Do
• mituot03
• iandithuhoai25
• bbvipb
• tops2liz
• maitienluat
• ........? còn không

em nhớ em đăng ký rồi mà

Mình xin đóng góp một đề:
ĐỀ 8: ĐỀ THI HSG TP Hồ Chí Minh
Năm học: 1989 - 1990
Vòng 1:
Bài 1: Cho hai số nguyên dương $a$ và $b$ ($a \geq b$) đều không chia hết cho $5$. Chứng minh rằng $a^4-b^4$ $\vdots$ $5$.
Bài 2: Tìm tất cả các cặp số tự nhiên $x$, $y$ sao cho: $\sqrt{x}+\sqrt{y} = \sqrt{1989}$.
Bài 3: Chứng minh rằng nếu $a$, $b$, $c$ là chiều dài ba cạnh một tam giác thì:
$ab + bc + ac \leq a^2+b^2+c^2 < 2(ab+bc+ac)$.
Bài 4: Cho hình vuông $ABCD$ có tâm $O$, cạnh bằng $10 cm$. Gọi $I$ là một điểm bất kì nằm trên đường tròn đi qua ba điểm $A$, $O$, $D$ và ngoài hình hình vuông ($I$ không trùng với $A$ và $D$). $OI$ cắt cạnh $BC$ tại $J$. Cạnh $DK$ của hình bình hành $IJKD$ cắt $BC$ tại $E$. $EH$ là đường cao của tam giác $EKJ$.
a) Tính số đo của góc $HEK$.
b) Chứng minh rằng $IJ > 10\sqrt{2} cm$.

Mình post đề được không?

Cho em hỏi : Ai có thể biến $a^2 + b^2$ thành một hằng đẳng thức ?

$a^2+b^2=(a+b)^2-2ab=(a-b)^2+2ab$.
Nếu $a$ và $b$ cùng dấu:
$a^2+b^2=a^2+(\sqrt{2ab})^2+b^2-(\sqrt{2ab})^2=(a+b-\sqrt{2ab})(a+b+\sqrt{2ab})$

Đây là cách giải của mình:
Số cần tìm có dạng $\overline{abcabc}+1$. Đặt $\overline{abc}=x$ thì ta có $1001x+1=n^2 (1)$ (Với $n \in N$, $100 \leq x \leq 998$).
$x \geq 100$ nên $1001x +1 \geq 100101$, do đó $n \geq 317$. $x \leq 998$ nên $n \leq 999$.
Từ $(1)$ ta có $x=\frac{n^2-1}{1001}$
Quy trình: (xin lỗi vì mình không biết gõ ô vuông)
$A=A+1:B=\frac{A^2-1}{1001}$, $CALC$ $A=316$. Quy trình được lặp đến khi $B$ nguyên.

p/s:Bạn có được đi thi cấp Quốc Gia không?

Lúc đầu là $25$ người ngồi $21$ người đứng. Qua bến đầu thêm $4$ người lên nữa. Tổng số là $50$. $25$ người đứng, $25$ người ngồi.
Không biết có đúng không vì số hành khách phải có dạng $a=50k (k \in Z+)$ do $\frac{8}{100}=\frac{4}{50}$ mà theo quy định của luật giao thông thì $k<2$.

suy ra x=y, thay vào PT đầu bài, ta có:
$x^3-nx-n=0$
Theo công thức nghiệm Cácđanô, ta có $x=\sqrt[3]{\frac{n}{2}+\sqrt{\frac{n^2}{4}-\frac{n^3}{27}}}+\sqrt[3]{\frac{n}{2}-\sqrt{\frac{n^2}{4}-\frac{n^3}{27}}}$
Vậy hệ PT của bài có nghiệm duy nhất là $x=y=\sqrt[3]{\frac{n}{2}+\sqrt{\frac{n^2}{4}-\frac{n^3}{27}}}+\sqrt[3]{\frac{n}{2}-\sqrt{\frac{n^2}{4}-\frac{n^3}{27}}}$

Chưa chắc phương trình này có 1 nghiệm, bởi dùng công thức Cacdano ta chỉ tìm được 1 nghiệm của phương trình bậc 3.

Giải hệ phương trình:
$$\left\{\begin{matrix}
x^3=6(y+1)\\
y^3=6(x+1)
\end{matrix}\right.$$
Đề của
daovuquang

Bài làm của thanhluong:
$\left\{\begin{matrix} x^3=6(y+1) (1) \\ y^3=6(x+1) (2) \end{matrix} \right.$
Trừ $(1)$ cho $(2)$ vế theo vế, ta được:
$x^3-y^3=6(y-x) \Leftrightarrow (x-y)(x^2+xy+y^2)+6(x-y)=0$.
$\Leftrightarrow x-y=0$ (Vì $x^2+xy+y^2+6 \geq 6 \geq 0$ với mọi $x$, $y$).
$\Leftrightarrow x=y$.
Thay $x = y$ vào $(1)$, ta được:
$x^3-6x-6=0$
$\Leftrightarrow x^3-6-6(\sqrt[3]{4}+\sqrt[3]{2})-6x+6(\sqrt[3]{4}+\sqrt[3]{2})=0$.
$\Leftrightarrow x^3-(\sqrt[3]{4}+\sqrt[3]{2})^3+6(x-\sqrt[3]{4}-\sqrt[3]{2})=0$
$\Leftrightarrow (x-\sqrt[3]{4}-\sqrt[3]{2})(x^2+x(\sqrt[3]{4}+\sqrt[3]{2})+\sqrt[3]{4}+\sqrt[3]{2}+6)=0$.
$\Leftrightarrow x - \sqrt[3]{4} -\sqrt[3]{2}=0$.
$\Leftrightarrow x = \sqrt[3]{4}+\sqrt[3]{2}$.
Vậy: Hệ phương trình đã cho có nghiệm duy nhất $(\sqrt[3]{4}+\sqrt[3]{2}; \sqrt[3]{4}+\sqrt[3]{2})$

Điểm bài 10
S = 3 + 3*10 = 33

Cho em đăng ký với

Giải phương trình:
$$\frac{x-3x^{2}}{2}+\sqrt{2x^{4}-x^{3}+7x^{2}-3x+3}=2$$
Đề của
BlackSweet

Bài làm của thanhluong:
Phương trình đã cho tương đương với:
$2\sqrt{2x^{4}-x^{3}+7x^{2}-3x+3}=3x^2-x+4$
$\Rightarrow 4(2x^{4}-x^{3}+7x^{2}-3x+3)=(3x^2-x+4)^2$.
$\Leftrightarrow 8x^4-4x^3+28x^2-12x+12=9x^4+x^2+16-6x^3+24x^2-8x$.
$\Leftrightarrow x^4-2x^3-3x^2+4x+4=0$.
$\Leftrightarrow x^3(x-2)-3x^2+6x-2x+4=0$.
$\Leftrightarrow x^3(x-2)-3x(x-2)-2(x-2)=0$.
$\Leftrightarrow (x-2)(x^3-3x-2)=0$.
$\Leftrightarrow (x-2)(x^3+2x^2+x-2x^2-4x-2)=0$.
$\Leftrightarrow (x-2)[x(x+1)^2-2(x+1)^2]=0$.
$\Leftrightarrow (x-2)^2(x+1)^2=0$.
$\Leftrightarrow x=2$ hoặc $x=-1$.
Thử lại ta thấy đúng.
Vậy: Phương trình có tập nghiệm $S=\{ -1; 2 \}$.

_________________
@Joker: N ên ghi rõ ĐK căn thức có nghĩa
d=9

 

S = 6 + 9*3 = 33

Bài làm của thanhluong:

BỔ ĐỀ: Nếu $a, b, x, y$ là các số thực dương thì ta có bất đẳng thức:
$$\sqrt{a^2+x^2}+\sqrt{b^2+y^2} \geq \sqrt{(a+b)^2+(x+y)^2}$$.
Chứng minh:
Xét hiệu: $(a^2+x^2)(b^2+y^2)-(ab+xy)^2$
$=(ay-bx)^2 \geq 0, \forall a, b, x, y>0$.
$\Rightarrow (a^2+x^2)(b^2+y^2) \geq (ab+xy)^2$.
$\Rightarrow 2\sqrt{(a^2+x^2)(b^2+y^2)} \geq 2(ab+xy)$.
$\Leftrightarrow a^2+b^2+x^2+y^2+2\sqrt{(a^2+b^2)(x^2+y^2)} \geq a^2+b^2+x^2+y^2+2ab+2xy$.
$\Leftrightarrow (\sqrt{a^2+x^2}+\sqrt{b^2+y^2})^2 \geq (a+b)^2+(x+y)^2$.
$\Rightarrow \sqrt{a^2+x^2}+\sqrt{b^2+y^2} \geq \sqrt{(a+b)^2+(x+y)^2}$.
Bổ đề được chứng minh. Đẳng thức xảy ra khi và chỉ khi: $ay=bx \Leftrightarrow \frac{a}{x}=\frac{b}{y}$.

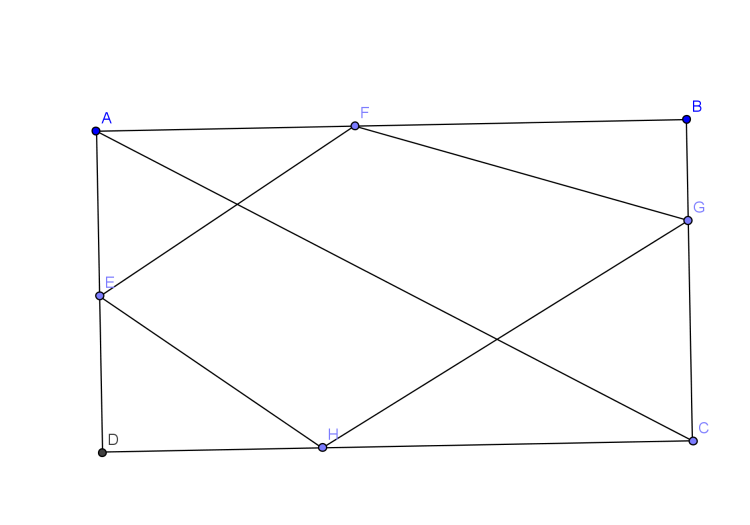
Trở lại bài toán, áp dụng định lí Pitago vào các tam giác vuông $\triangle{AEF}, \triangle{DEH}, \triangle{CHG}, \triangle{BFG}$, ta được:
$EF+FG+GH+HE=\sqrt{EA^2+FA^2}+\sqrt{BF^2+BG^2}+\sqrt{CH^2+CG^2}+\sqrt{DH^2+DE^2}$.
Hay: $P_{EFGH}=\sqrt{EA^2+FA^2}+\sqrt{BF^2+BG^2}+\sqrt{CH^2+CG^2}+\sqrt{DH^2+DE^2}$ $(1)$.
Sử dụng liên tiếp bổ đề phụ trên và định lý Pitago cho tam giác vuông $ABC$, ta được:
$\sqrt{EA^2+FA^2}+\sqrt{DE^2+DH^2}+\sqrt{BG^2+BF^2}+\sqrt{CG^2+CH^2} \geq \sqrt{AD^2+(FA+DH)^2}+\sqrt{BC^2+(BF+CH)^2} \geq \sqrt{(AD+BC)^2+(AB+CD)^2}=2\sqrt{AB^2+BC^2}=2AC$: Không đổi $(2)$.
Từ $(1)$ và $(2)$ suy ra $P_{EFGH} \geq 2AC$. Đẳng thức xảy ra khi và chỉ khi:
$\left\{\begin{matrix} \frac{AF}{DH}=\frac{AE}{DE} &&\\ \frac{BF}{CH}=\frac{BG}{CG} &&\\ \frac{AF+DH}{BF+CH}=\frac{AD}{BBC} \end{matrix}\right.$ $(*)$
Vậy: Chu vi tứ giác $EFGH$ đạt giá trị nhỏ nhất bằng $2AC$ khi các điểm $F$, $G$, $H$ thoả $(*)$. ( Nên nêu rõ để suy ra EFGH là hình bình hành)

___________________________________
@Joker: Nên lập luận rõ chỗ cuối
d=9
S = 12+3*9 = 39

Đề bài:
Cho tam giác $ABC$. Đường thẳng $d$ đi qua trọng tâm $G$ của tam giác cắt các cạnh $AB$, $AC$ lần lượt ở $E$ và $F$. Tính tổng:
$$S=\frac{AB}{AE}+\frac{AC}{AF}$$

Đáp án:

Gọi $M$ là trung điểm $BC$. Từ $B$ kẻ $BD//AM$, từ $C$ kẻ $CK//AM$ ($C$ và $K$ nằm trên đường thẳng $d$). Suy ra $BD//CK//AM$.

$BD//AG$ nên áp dụng định lý Ta-lét, ta có:
$$\frac{BD}{AG}=\frac{AE}{BE}$$
$$\Rightarrow \frac{BD}{AG}+1=\frac{AE}{BE}+1$$
hay $$\frac{BD}{AG}+1=\frac{AB}{AE}$$ (1)

Tương tự, đối với tam giác $FKC$ thì:
$$\frac{AF}{FC}=\frac{CK}{AG}$$
$$\Rightarrow \frac{AC}{CF}=\frac{CK}{AG}+1$$ (2)

Cộng (1) và (2) vế theo vế, ta được:
$$\frac{AB}{AE}+\frac{AC}{CF}=\frac{CK+BD}{AG}+2$$

Lại có $BD//CK$ nên $BDKC$ là hình thang.

$M$ là trung điểm $BC$ và $MG//BD//CK$ $\Rightarrow GM$ là đường trung bình của hình thang $BDKC$.
Nên $CK+BD=2GM$.

$G$ là trọng tâm của tam giác $ABC$ nên $AG=2GM$, do đó $BD+CK=AG$.
$$\Rightarrow S=\frac{AB}{AE}+\frac{AC}{AF}=\frac{AG}{AG}+2=1+2=3$$.

Bài làm của thanhluong:
$$x^2-5x+7=3^y (1)$$.
-Với $y=0$, phương trình $(1)$ được viết lại thành: $x^2-5x+6=0 \Leftrightarrow (x-2)(x-3)=0 \Leftrightarrow x=2$ hoặc $x=3$.
Với $y=1$, phương trình $(1)$ được viết lại thành: $x^2-5x+4=0 \Leftrightarrow (x-1)(x-4)=0 \Leftrightarrow x=1$ hoặc $x=4$.
Với $y \geq 2$, ta có: $\Delta_{(1)}=(-5)^2+4 \cdot 1 \cdot (7-3y)=3(4 \cdot 3^{y-1}+1)$.
Phương trình $(1)$ có nghiệm tự nhiên với $y \geq 2$ khi và chỉ khi $\Delta_{(1)}$ là số chính phương.
Mà $(3, 4 \cdot 3^{y-1}+1)=1$ nên $3$ là số chính phương. Điều này vô lý, do đó phương trình vô nghiệm tự nhiên với $y>2$.
Vậy: Phương trình có các cặp nghiệm tự nhiên $(x; y) \in \{ (2;0), (3;0), (1;1), (4;1) \}$.
----
$S=\left \lfloor \frac{52-\left ( 59-19 \right )}{2} \right \rfloor+3.10+0+0=35$

Đề bài:
Giải phương trình nghiệm nguyên:
$15x^4-37x^2y^2-84x^2+14y^4+53y^2=-45$

Giải:
Bổ đề: Số chính phương lẻ chia $8$ dư $1$
Thật vậy. với $k \in Z$ ta luôn có
$(2k+1)^2=4k^2+4k+1 =4k(k+1)+1\equiv 1$ (mod $8$) (Vì $k(k+1) \equiv 0$ (mod $2$))

Trở lại bài toán, phương trình trên đề bài đương với:
$(x^2-2y^2-5)(15x^2-7y^2-9)=0$
$\Leftrightarrow x^2-2y^2-5=0$ hoặc $15x^2-7y^2-9=0$.
Trường hợp 1: $x^2-2y^2-5=0$
Khi đó $x^2-2y^2=5 \rightarrow x^2=2y^2+5 \rightarrow x^2$ lẻ.
Áp dụng bổ đề trên, ta suy ra $x^2$ chia $8$ dư $1$, đặt $x^2=8m+1$ ($m \in Z$), ta có:
$8m+1+2y^2=5 \Leftrightarrow 8m+2y^2=4 \Leftrightarrow 4m+y^2=2$
Nên $y^2$ chia hết cho $2$ và không chia hết cho $4$, suy ra điều vô lý vì số chính phương chia hết cho $2$ luôn chia hết cho $2^2=4$.
Trường hợp 2: $15x^2-7y^2-9=0$
Khi đó $15x^2-2=7y^2+7=7(y^2+1)$ nên $15x^2-2$ chia hết cho $7$. (*)

Nếu $x \equiv 0$ (mod $7$) $\Rightarrow 15x^2 \equiv 0$ (mod $7$) $\Rightarrow 15x^2-2$ không chia hết cho $7$.
Nếu $x \equiv \pm 1$ (mod $7$) $\Rightarrow x^2 \equiv 1$ (mod $7$) $\Rightarrow 15x^2 \equiv 15$ (mod $7$) $\Rightarrow 15x^2-2$ không chia hết cho $7$.
Nếu $x \equiv \pm 2$ (mod $7$) $\Rightarrow x^2 \equiv 4$ (mod $7$) $\Rightarrow 15x^2 \equiv 60$ (mod $7$) $\Rightarrow 15x^2-2$ không chia hết cho $7$.
Nếu $x \equiv \pm 3$ (mod $7$) $\Rightarrow x^2 \equiv 9$ (mod $7$) $\Rightarrow 15x^2 \equiv 135$ (mod $7$) $\Rightarrow 15x^2-2$ không chia hết cho $7$.
Do đó với mọi $x \in Z$, $15x^2-2$ không chia hết cho $7$, mâu thuẫn với (*).

Vậy Phương trình đã cho vô nghiệm nguyên

Đề bài
Cho $x$,$y$ là các số nguyên dương thoả mãn phương trình:
$$2x^2+x=3y^2+y$$.
Chứng minh rằng: Các số $x-y$, $2x+2y+1$ và $3x+3y+1$ đều là các số chính phương.







Đáp án:
Từ: $2x^2+x=3y^2+y$
$\Leftrightarrow 2x^2-2y^2+x-y=y^2\Leftrightarrow (x-y)(2x+2y+1)=y^2$.

Gọi $d$ là ước chung lớn nhất của $x-y$ và $2x+2y+1$.
$\Rightarrow y^2$ $\vdots$ $d^2 $ $\Rightarrow y$ $\vdots$ $d$.

Mà $x-y$ $\vdots$ $d$ $\Rightarrow x$ $\vdots$ $d$ $\Rightarrow 2x$ $\vdots$ $d$ và $2y$ $\vdots$ $d$.

Lại có $2x+2y+1$ $\vdots$ $d$ $\Rightarrow 1$ $\vdots$ $d \Rightarrow d=1$

Mà $(x-y)(2x+2y+1)=y^2$, nên cả $x-y$ và $2x+2y+1$ đều là các số chính phương. (1)

Mặt khác: $3x^2-3y^2+x-y=x^2$
$\Leftrightarrow (x-y)(3x+3y+1)=x^2$

Chứng minh tương tự như trên, suy ra được $x-y$ và $3x+3y+1$ đều là số chính phương. (2)

Từ (1) và (2) ta có điều phải chứng minh.

Mình đã thử đến 20 chữ số cũng ok , nhưng có một lỗi nhỏ , đến chỗ: "Thoat khoi chuong trinh (yes/no)?" mà ghi "no" cũng bị thoát ra.

để mình fix

Đây là phần mềm do bạn Trần Hoàng Long (Lớp C04 trường THPT Nguyễn Thượng Hiền) viết. Mọi người download về sử dụng thử và cho ý kiến.
http://www.mediafire...fc6a96j4l6vqyg9

Cái này hay
Nhưng nếu lập trình bằng ngôn ngữ Pascal thì sẽ có nhược điểm là nếu nhập số quá lớn (vượt qua longint) thì sẽ bị thoát ra luôn.

Hihi em mới viết chương trình này có thể kiểm tra được số lớn đến vài ngàn chữ số, mọi người tải về dùng thử rồi cho ý kiến được không ạ
http://www.mediafire...wt309ze39niwenq

không có nghĩa là số "456457,4646" số thập phân ế thì nó vẫn phang kết quả, kiểu dữ liệu đó tuy rộng nhưng nó là số thực :|, để hoàn chỉnh hơn mình nghĩ bạn nên dùng lệnh repeat ép người dùng nhập số vào phải là số nguyên thì hay hơn
nhưng nếu gãnh bạn share code cho mình dc ko, tuy hổng chỗ đó nhưng có thể mình sẽ chỉnh dc cho bạn, với lại tham khảo

Em không dùng Pascal để viết mà dùng Python 2.7 nên không có lệnh repeat anh à, nhưng dù sao thì đó cũng không phải là vấn đề lớn, em sẽ fix lại. Code cũng tựa như Pascal ấy anh.

p/s: cho em xin Y!M hay Facebook của anh rồi nói chuyện cho tiện ạ

Mình đã tìm ra 1 lỗi cực kì nghiêm trọng trong code này đó là bạn đã sử dụng kiểu dữ liệu ectended ( đoán maybe ), vì khi nhập 4546457,4646 thì nó cũng phang kết quả @@, mình đang nghiên cứu vấn đề này :-?

Em không hiểu cho lắm? đúng là 2 số trên không phải là số nguyên tố mà anh?

Nếu $a=4$:

Ta có $F=(x+2y+1)^2+(2x+4y+5)^2$.

Đặt $x+2y+1=k$ $\Rightarrow F=k^2+(2k+3)^2=5k^2+12k+9=5(k+\frac{6}{5})^2+\frac{9}{5} \geq \frac{9}{5}$

Dấu '=' xảy ra $\Leftrightarrow k=-\frac{6}{5}$

$\Leftrightarrow x+2y=-\frac{11}{5}$

Nếu $a \neq 4$:

Ta có $F=(x+2y+1)^2+(2x+ay+5)^2 \geq 0+0=0$ $\forall x, y$.

Dấu '=' xảy ra $\Leftrightarrow x+2y+1=0$ và $2x+ay+5=0$.
$\Leftrightarrow 2x+4y+2=0$ và $2x+ay+5=0$

$\Rightarrow (2x+4y+2)-(2x+ay+5)=0$

$\Rightarrow y=\frac{3}{4-a}$.

$\Rightarrow x=\frac{10-a}{a-4}$

Vậy: Nếu $a=4$ thì $\min{F}=\frac{9}{5}$ tại $x=-\frac{11}{5}-2y$ (Với $y$ là số thực bất kỳ).

Nếu $a \neq 4$ thì $\min{F}=0$ tại $x=\frac{10-a}{a-4}$ và $y=\frac{3}{4-a}$.
----
$S=52-(23-21)+3.10+10+0=90$

Mở rộng của thanhluong:

Tùy theo giá trị của $e$, $(e\neq 0)$ hãy tìm giá trị nhỏ nhất của biểu thức:

$$A =(ax +by+c)^2 +(dx+ey+f)^2$$ $$(a,b,c,d,f \neq 0, \frac{bd}{a}\neq e)$$
Bài giải:

$A=(ax+by+c)^2 +(dx+ey+f)^2$

Vì $(ax+by+c)^2 \geq 0 \vee a,b,y,c \neq 0$

và $(dx+ey+f)^2 \geq 0 \vee f,d,x,e,y, \neq 0$

$\Rightarrow A \geq 0 \vee f,b,y,c,d,x,e, \neq 0$

Dấu "$=$" xảy ra khi và chỉ khi:

$\left\{\begin{matrix} ax+by+c=0 & \\ dx+ey+f =0 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} x=\frac{-c-by}{a} (1) & \\ dx+ey+f =0 (2)& \end{matrix}\right.$

Thế (1) vào (2)

Ta có :

$d \cdot \frac{-c-by}{a} +ey+f =0$

$\frac{-dc}{a} -\frac{bdy}{a} +ey +f =0$

$y \cdot (e-\frac{bd}{a}) =\frac{dc}{a} -f$

$y=\frac{\frac{dc}{a} -f}{e-\frac{bd}{a}}$

$y=\frac{dc-fa}{ea-db}$

$\Rightarrow x =\frac{-c-b\frac{dc-fa}{ea-db}}{a}$

$x =\frac{-c-\frac{bdc-fba}{ea-db}}{a}$

$x =\frac{\frac{-cea+cdb-bdc+fba}{ea-db}}{a}$

$x=\frac{fba-cea}{ea^2-dba}$

$x=\frac{fb-ce}{ea-db}$

Vậy $\min{A} =0$ $\Leftrightarrow \left\{\begin{matrix} x=\frac{fb-ce}{ea-db} & \\ y=\frac{dc-fa}{ea-db} & \end{matrix}\right.$

Lời giải của toán thủ ConanTM:
Đặt: S(a) = $a^2-a-b^2$. Giả sử S(a) là số chính phương thì S(1-a) cũng là số chính phương mà a và 1 - a khác tính chẵn lẻ => Mâu thuẫn vì theo giả thiết thì a và b phải cùng tính chẵn lẻ. (đpcm)

Theo mình thì không thể xét $S(1-a)$ được vì để $1-a$ là số tự nhiên thì $a \leq 1 \Rightarrow b \leq 0 \Rightarrow b=0$ và $a=0$ hoặc $a=1$.

Mở rộng của thanhluong:

Tùy theo giá trị của $e$, $(e\neq 0)$ hãy tìm giá trị nhỏ nhất của biểu thức:

$$A =(ax +by+c)^2 +(dx+ey+f)^2$$ $$(a,b,c,d,f \neq 0, \frac{bd}{a}\neq e)$$
Bài giải:

$A=(ax+by+c)^2 +(dx+ey+f)^2$

Vì $(ax+by+c)^2 \geq 0 \vee a,b,y,c \neq 0$

và $(dx+ey+f)^2 \geq 0 \vee f,d,x,e,y, \neq 0$

$\Rightarrow A \geq 0 \vee f,b,y,c,d,x,e, \neq 0$

Dấu "$=$" xảy ra khi và chỉ khi:

$\left\{\begin{matrix} ax+by+c=0 & \\ dx+ey+f =0 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} x=\frac{-c-by}{a} (1) & \\ dx+ey+f =0 (2)& \end{matrix}\right.$

Thế (1) vào (2)

Ta có :

$d \cdot \frac{-c-by}{a} +ey+f =0$

$\frac{-dc}{a} -\frac{bdy}{a} +ey +f =0$

$y \cdot (e-\frac{bd}{a}) =\frac{dc}{a} -f$

$y=\frac{\frac{dc}{a} -f}{e-\frac{bd}{a}}$

$y=\frac{dc-fa}{ea-db}$

$\Rightarrow x =\frac{-c-b\frac{dc-fa}{ea-db}}{a}$

$x =\frac{-c-\frac{bdc-fba}{ea-db}}{a}$

$x =\frac{\frac{-cea+cdb-bdc+fba}{ea-db}}{a}$

$x=\frac{fba-cea}{ea^2-dba}$

$x=\frac{fb-ce}{ea-db}$

Vậy $\Min{A} =0$ $\Leftrightarrow \left\{\begin{matrix} x=\frac{fb-ce}{ea-db} & \\ y=\frac{dc-fa}{ea-db} & \end{matrix}\right.$

Đề của BTC:
Giải phương trình:
$$2\sqrt[3]{(1+x)^2}+3\sqrt[3]{1-x^2}+\sqrt[3]{(1-x)^2}=0$$

Phương trình tương đương:
$2\sqrt[3]{x+1}\sqrt[3]{x+1}+2\sqrt[3]{(1+x)(1-x)}+\sqrt[3]{1-x}\sqrt[3]{1-x}=0$

$\Leftrightarrow 2\sqrt[3]{x+1}(\sqrt[3]{x+1}+\sqrt{1-x})+\sqrt[3]{1-x}(\sqrt[3]{1+x}+\sqrt[3]{1-x})=0$.

$\Leftrightarrow (\sqrt[3]{1+x}+\sqrt[3]{1-x})(2\sqrt[3]{1+x}+\sqrt[3]{1-x})=0$.

$\Leftrightarrow \sqrt[3]{1+x}+\sqrt[3]{1-x}=0$ hoặc $2\sqrt[3]{1+x}+\sqrt[3]{1-x}=0$.

$\boxed{\text{Trường hợp 1}}$: $\sqrt[3]{1+x}+\sqrt[3]{1-x}=0$

Khi đó $\sqrt[3]{1+x}=-\sqrt[3]{1-x}$ $\Leftrightarrow 1+x = -1+ x$ (Vô lý).

$\boxed{\text{Trường hợp 2}}$: $2\sqrt[3]{1+x}+\sqrt[3]{1-x}=0$

Khi đó $2\sqrt[3]{1+x}=-\sqrt[3]{1-x}$ $\Leftrightarrow 8(1+x)=-1+x \Leftrightarrow x=-\frac{9}{7}$

Vậy: $\boxed{S=\{ -\frac{9}{7} \}}$
----
Điểm bài làm: 10
Tổng điểm: $\left [ \dfrac{52-\left ( 21-20 \right )}{2} \right ]+3.10+0+0=45$

Đặt
$|a_1-b_1|+|a_2-b_2|+...+|a_{1006}-b_{1006}|=A$.

Theo giả thiết, với số tự nhiên $i$, $1\leq i \leq 1006$ thì $|a_i-b_i|$ có tận cùng là $6$ hoặc $1$

Nên ta đặt $|a_i-b_i|=5n_i+1$ (với $n_i$ là số tự nhiên)

Thay $|a_i-b_i|=5n_i+1$ với $i=1, 2, 3,...,1006$ vào $A$, ta có:

$A=5n_1+1+5n_2+1+...+5n_{1006}+1$

$=5(n_1+n_2+n_3+...+n_{1006}) + 1006$

$\Rightarrow A=5(n_1+n_2+n_3+...+n_{1006}) + 10^3 + 6$ (1)

Giả sử có trong hai tập {$a_1, a_2, a_3,...a_{1006}$} và {$b_1, b_2, b_3,...b_{1006}$} có $2u+1$ ($u$ là số tự nhiên) cặp $(a_i, b_i)$ sao cho $|a_i-b_i|=5n_i+1$ ($n_i$ là số lẻ), tức là $|a_i-b_i|$ có chữ số tận cùng là $1$.

Suy ra $a_i-b_i=5k_i+1$ (với $k_i$ là số nguyên chia hết cho $2$).

Từ đó ta có $b_i=a_i-5k_i-1 \Rightarrow a_i+b_i=2a_i-5k_i-1$, nên $a_i+b_i$ không chia hết cho $2$.

Do đó tổng của các số $a_i$, $b_i$ (sao cho $|a_i-b_i|$ có chữ số tận cùng là $1$) cũng là một số không chia hết cho $2$.

Mặt khác, tổng các số $a_i$, $b_i$ còn lại trong $2$ tập trên đều chia hết cho $2$.

Suy ra:
$a_1+b_1+a_2+b_2+...+a_i+b_i+...+a_{1006}+b_{1006}$ cũng không chia hết cho $2$.

Hay $1+2+3+...+2012$ không chia hết cho

$2$ (Vô lý vì $1+2+3+...+2012=\frac{2012 \cdot 2013}{2}=1006 \cdot 2013$ $\vdots$ $2$)

Từ mâu thuẫn trên ta thấy rằng số cặp $(a_i, b_i)$, để $|a_i-b_i|$ có tận cùng là $1$, không phải là số lẻ. Vì vậy tổng các giá trị $|a_i-b_i|$ trên phải là số chẵn.

Nên $n_1+n_2+n_3+...+n_{1006}$ phải là số chẵn, ta đặt $n_1+n_2+n_3+...+n_{1006} = 2v$ ($v$ là số tự nhiên).

$\Rightarrow 5(n_1+n_2+n_3+...+n_{1006})=10v$ (2)

Từ (1) và (2) suy ra:

$A = 10v+10^3+6$ (với $v$ là số tự nhiên).

Vậy: Biểu thức $|a_1-b_1|+|a_2-b_2|+|a_3-b_3|+...+|a_{1006}-b_{1006}|$ có chữ số tận cùng là $6$.
----
Điểm bài làm:
$S=48-\left ( 27-19 \right )+3.9+0+0=67$