Hỏi mãi bạn không giảng hộ mình , đành up lên vmf vậy
cho a,d nguyên dương
xét tất cả các số có dạng: a,a+d,a+2d,...,a+nd,......
cmr trong các số đó có ít nhất một số mà 4 chữ số đầu tiên của nó là 1991

Móc lại bài từ năm 2005 =)
Lấy H là trung điểm AB
$FI \perp AB$
Dễ thấy F và Q ở cùng phía với EH
Vậy$ \angle AQE =\angle BQF \rightarrow \angle FQI =\angle EQH$
$\rightarrow \Delta FQI $~$\angle EQH$
$\rightarrow \frac{IQ}{QH} =\frac{FI}{EH}$
$\rightarrow \frac{IQ}{IH}=\frac{FI}{FI +EH}$
$\rightarrow IQ =\frac{FI.IH}{FI +EH}$ (cố định)
$\rightarrow$ Điểm Q ở trên BC và cách I 1 khoảng $\frac{FI.IH}{FI +EH}$

C,Dễ dàng cm CD là tiếp tuyến của 2 đường tròn tâm E và tâm F
$S_{CDEF} = CD .\frac{R}{2} =MH .\frac{R}{2}=\frac{S_{MBA}}{2}$
Mà$ \frac{S_{MBA}}{S_{M'BA}} =\frac{MH^2}{M'O^2} \leq 1$
$\rightarrow S_{CDEF} \leq \frac{S_{M'BA}}{2}=\frac{R^2}{2}$
dấu "=" sảy ra $\leftrightarrow $$H\equiv O, M\equiv M'$
D,
ta có $S_{MCHD} =2S_{CMD}$
Dễ dàng cm $\Delta MCD ~~\Delta MBA$
$\rightarrow \frac{S_{MCD}}{S_{MBA}} =\frac{AH^2}{2 AO^2} \leq \frac{1}{4} $
$\rightarrow \frac{S_{MCHD}}{S_{MBA}}\leq \frac{1}{2}$
Mà$ \frac{S_{MBA}}{S_{M'BA}} =\frac{MH^2}{M'O^2} \leq 1$
$\rightarrow \frac{S_{MCHD}}{S_{M'BA}}=\frac{1}{2}$
$\rightarrow S_{MCHD} \leq \frac{R^2}{2}$
dấu "=" sảy ra $\leftrightarrow $$H\equiv O, M\equiv M'$

Cách hay câu b:
dễ thấy$ \frac{EG}{GF} =1$ ,$\frac{BC}{BE} .\frac{FD}{FC}=1$
Nhân vào ta có$ \frac{EG.BC.FD}{GF.BE.FC} =1$
Theo Meneluos ta có D,G,B thẳng hàng $\rightarrow DPCM$

Đổi 10,2 km =10200m
4,4km=4400m
khi người thứ 2 bắt đầu đi thì oto 1 đẫ đi dc : 3600
Khoảng cách 2 người lúc này là :10200-3600= 6600m
Hiệu vận tộc 2 người là ;2m/s
Để 2 người cách nhau 4.4 km thì họ phải đi mất :(chưa gặp nhau)
TH1 :$\frac{6600-4400}{10+12}=100s$
khi đó là lúc :8h và 100s nữa
lúc đó người 1 cách A 1260m,cách B:4540m
về người 2 cũng tương tự
Trường hợp 2 cũng tương tự:
.....

Em cũng như nhiểu bạn ở trên VMF cũng cùng 1 câu hỏi :" Sách nào hay , Sách nào quý " .Nhưng vẫn chưa tìm ra câu trả lời phù hợp ,với lại sách quý thì rất khó tìm :-? .Em lập topic này để cùng chia sẻ các loại sách , dạng PDF thì càng tốt ^^.Em xin cảm ơn .
Hiện giở ai có file PDF những sách như :"Những Viên Kim Cương " ,"Cẩm nang vẽ Hình phụ" của Thầy Tấn ,"Sáng Tạo BDT" của Thầy Hùng , hoặc những quyển BDT của Võ Quốc Bá Cẩn,Trần Phương,Trần Quốc Anh v..v thì share cho mọi người nhá .Em cảm ơn .

Bài 74
Coi x là số lớn nhất trong x,y,z
TH1 :
$x \geq y \geq z$(1)
$\rightarrow x^{19} \geq y^{19} ,y^5 \geq z^5$
$\rightarrow 1890z +z^{2001} \geq 1890x +x^{2001}$
$\rightarrow 1890(z-x) +z^{2001} -x^{2011} \geq 0$
$\rightarrow z \geq x$(2)
Từ (1) và (2) $\rightarrow x=y=z$
TH2 :$x \geq z \geq y$(3)
$\rightarrow z^{19} \geq y^{19} ,x^5 \geq z^5$
$\rightarrow 1890y +y^{2001} \geq 1890x+x^{2001}$
$\rightarrow 1890(y-x) +y^{2001} -x^{2001} \geq 0$
$\rightarrow y\geq x(4)$
Từ (3) và (4) $\rightarrow x=y=z$
Vậy cả 2 trường hợp $\rightarrow x=y=z$
Nếu x=y=z =0 thì thoả mãn
Nễu x=y=z khác 0
Thì
$x^{18} +x^4 =1890 +x^{2000}$
Ta có :nếu x=1 và -1 thì sai
Nếu $x \geq 2$ hoặc $x \leq -2$ thì$ x^{2000} \geq x^{18} +x^4$$ \rightarrow$ loại nuốt
$\rightarrow x=y=z=0$

Bài này kinh thật, và đây là kết quả chuẩn:
$\frac{1}{4\sqrt[3]{4}+2\sqrt[3]{2}-16}=-\frac{15}{191}-\frac{4\sqrt[3]{2}}{191}-\frac{17\sqrt{4}}{764}$

Vậy đề như vậy có làm dc ra như anh nthoangcute không??
(p/s cho mình hỏi: có phải tất cả các p/s đều có thể trục căn không)

Bạn ơi đề đúng đấy,không sai đâu,nếu để thế này mới khó chứ .Mình gợi ý kết quả này :[/size]
$\frac{15\sqrt[3]{4}-68}{764}$

Có vẻ cách bạn sai :|
không tin vào đây xem kq =))
http://www.wolframal...\sqrt[3]{2}-16}
Và
http://www.wolframal...[3]{4}-68}{764}

Trục căn thức ở mẫu sau:$\frac{1}{4\sqrt[3]{4}+2\sqrt[3]{2}-16}$

Mình nghĩ đề là $\frac{1}{4\sqrt[3]{4}+2\sqrt[3]{2}+16}$
Gọi$ \sqrt[3]{2} =a$
$\rightarrow a^3 =2$
$\rightarrow BT \leftrightarrow \frac{2}{8a^2+4a+16a^3} =\frac{a^3}{4a(2a+1+4a^2)} =\frac{a^2.(2a-1)}{4.((2a)^3-1)} $
=$\frac{\sqrt[3]{4}.(2\sqrt[3]{2} -1)}{60}$

Bài Làm :

Bài toán tương đương số nghiệm của hệ phương trình

$\left\{\begin{matrix} x+y+z+t =32 \\ x,y,z,t \in N* \\ x\neq y \neq z \neq t \end{matrix}\right.$

$\Leftrightarrow $$\left\{\begin{matrix} x-1+y-1+z-1+t-1 =28 \\ x,y,z,t \in N* \\ x\neq y \neq z \neq t \end{matrix}\right.$

$\Leftrightarrow $$\left\{\begin{matrix} a+b+c+d =28 \\ a,b,c,d :\text{Không âm} \\ a \neq b \neq c \neq d \end{matrix}\right.$

Ta xét phần bù .

( Ở đây ta xét tính thứ tự của a,b,c,d)

Số nghiệm không âm của phương trình a+b+c+d =28 là 4495

Trước hết ta tính số nghiệm không âm của phương trình a+b+c+d=28 với :$\begin{pmatrix} 31 \\ 3\end{pmatrix}$ =4495

 @~ > Với chỉ đúng 2 số trong 4 số bằng nhau .Không mất tính tổng quát giả sử 2 số đó là $a=b=k ( 0 \leq k \leq 14)$

$\Rightarrow c+d =28 -2k$

Để có đúng 2 số bằng nhau thì ta loại đi trường hợp $c=d  \neq 7$ ( xảy ra khi $0 \leq k \leq 14 ,k \neq 7$) ( có 14 trường hợp như vậy ) và Chỉ 1 trong 2 só $c,d =k$ ( chỉ xảy ra khi $0 \leq k\leq 9 và k \neq 7$) (có 18 trường hợp như vậy) và loại đi trường hợp $k=c=d$ ( chỉ xảy ra khi $ k=7$).( có 1 trường hợp như vậy )

Tóm lại ta phải loại đi 33 trường hợp .

Số nghiệm không âm của phương trình c+d =28 -2k với (0\leq c ,d \leq 28-2k , k chạy từ 0 đến 14) là $\sum (28-2k +1) =225$

Tóm lại với a=b thì số nghiệm không âm của phương trình $a+b+c+d =28$ là :$225 -33 =192$

Như vậy tổng cộng có 1152 nghiệm không âm của phương trình $a+b+c+d =28$ mà chỉ có đúng 2 số bằng nhau.

@~> Với chỉ đúng 3 số trong 4 số bằng nhau .Không mất tính tổng quát giả sử 3 số đó là $a=b=c=k (0 \leq k\leq9)$

$\Rightarrow d =28 -3k$

Để có đúng 3 số bằng nhau thì ta loại đi trường hợp $d= k$ nghĩa là $k =7$ .Vậy chỉ loại đi 1 trường hợp.

Vậy số nghiệm không âm  của phương trình $a+b+c+d=28$ có đúng 3 số bằng nhau là $9x4 =36.$

@~> Với đúng 4 số bằng nhau ( 1 trường hợp)

@~> Với đúng 2 cặp 2 số bằng nhau  ( 2 cặp này khác nhau ) Không mất tính tổng quát giả sử $a=b=k ,c=d =t (k \neq t)$

Khi đó $k+t =14$ khi đó có 14 trường hợp

Vậy số nghiệm không âm của phương trình $a+b+c+d =28$ với 2 cặp 2 số bằng nhau ( 2 cặp khác nhau) là $14x3 =42$

Tóm lại số nguyệm không âm có ít nhất 2 số bằng nhau của phương trình $a+b+c+d =28$ là $1152+36+42+1=1231$

Vậy số nghiệm không âm đôi 1 khác nhau của phương trình $a+b+c+d =28$ là $4495-1231=3264$

Do a,b,c,d ở trên ta xét có tính thứ tự 

Nên số cách chia kẹo vào các hôp không tính thứ tự là 3264 :24= 136 cách.

Tóm lại Số cách chia kẹp vào các hộp sao cho mỗi hộp có số lượng kẹo khác nhau là 136 cách chia .

 

____________________________

NX: Sai về cách trình bày ký hiệu đôi một khác nhau (- 1đ )

Điểm bài: $d=9$

Điểm thưởng $d_t=8$

Điểm mở rộng $d_{mr}=0$

Điểm thảo luận $d_{tl}=0$

$S = \left \lfloor\frac{52 - \left (t_{lb} - t_{rd} \right )}{3} \right \rfloor+3\times d+d_{mr}+d_{t}+d_{tl}=\left \lfloor\frac{52 - 42}{3} \right \rfloor+3\times 9 +0+8+0=38$

Bài Làm :

Bài toán tương đương số nghiệm của hệ phương trình

Giải phương trình nghiệm nguyên:$x^2+y^2+z^2=x^2y^2$

Toán thủ ra đề: vutuanhien

Bài Làm :

Nếu x,y đều lẻ thì $x^2 \equiv 1$ mod 4 , $y^2 \equiv 1$ mod 4 $\Rightarrow x^2 +y^2 \equiv 2$ mod 4 Còn $(xy)^2 \equiv 1$ mod  4.

Như vậy $z^2 \equiv 3$ mod 4 $\Rightarrow$ vô lý 

Vậy ít nhất  một trong 2 số x,y là chẵn.

Xét x chẵn  Ta có:  $(xy)^2 \vdots 4 \Rightarrow y^2+z^2 \vdots 4 \Rightarrow$ y và z cùng chẵn.

Như vậy cả x,y,z đều chẵn.

Đặt $x =2x_1 ,y=2y_1 , z =2z_1 ( x_1 ,y_1 ,z_1 \in Z)$

Thay vào đề bài ta có $x_1^2 +y_1^2 +z_1^2 = 4 x_1^2.y_1^2$

Bởi 1 số chính phương chia 4 chỉ dư 0,1

$\Rightarrow x_1^2 +y_1^2 +z_1^2 = 4 x_1^2.y_1^2$

$\Leftrightarrow x_1 ,y_1 ,z_1$ chẵn

Đặt $x_1 =2x_2 ,y_1 =2y_2 ,z_1 =2z_2 (x_2 ,y_2 ,z_2 \in Z)$

Thay vào ta lại có $x_2 ^2 +y_2^2 +z_2^2 =16 x_2^2y_2^2$

Lặp lại quá trình như vậy sẽ dẫn đến $x \vdots 2^k ,y \vdots 2^k ,z \vdots 2^k (k \in Z)$

Điều này chỉ đúng khi $x=y=z=0$

Vậy nghiệm của phương trình nghiệm nguyên là $x=y=z=0$

Bài làm :

Từ Phương Trình (1) $\Rightarrow x \neq 1 , y \neq -1$

Từ Phương Trình (1) $\Rightarrow |x-1| .|y+1| =1 \Rightarrow |x-1| =\frac{1}{|y+1|}$

$\Rightarrow x =\frac{1}{|y+1|}+1 hoặc x= \frac{-1}{|y+1|} +1$ 

Thay vào Phương trình (2) $ \Rightarrow \frac{1}{|y+1|} -m|y+1| \leq m-1$

$\Leftrightarrow 1-m(y+1)^2 \leq (m-1)|y+1|$

$\Leftrightarrow m(y+1)^2 +(m-1)|y+1| -1\geq 0$

$\Leftrightarrow (|y+1|+1)(m|y+1|-1) \geq 0$

Ta có $ |y+1| +1 \geq 0 \forall y $

Nếu m \leq 0 \Rightarrow hệ bất phương trình vô nghiệm.

Nếu m >0

$\Rightarrow |y+1| \geq \frac{1}{m}$

$\Rightarrow y \geq \frac{1}{m}-1$ hoặc $ y \leq \frac{-1}{m} -1 $

Và $x=\frac{1}{y+1}+1 hoặc x =\frac{-1}{y+1} +1$

( $y \neq -1$)

Tóm lại với $m \leq 0 \Rightarrow$ Hệ bất phương trình vô nghiệm.

Với $m > 0 \Rightarrow$ hệ bất phương trình có nghiệm (x,y) =($\frac{\pm1}{y+1}+1,$ $y \neq -1$ và$ y \geq \frac{1}{m} -1$ hoặc $ y \leq \frac{-1}{m}-1$) ,

 

 

 

 

Mở rộng :
Thực chất bài toán là : $f(x+y) -f(xy) =f(x) +f(y)-f(x)f(y) \forall x,y \in R$ với 2 biến $x,y$

vậy ta thử nâng lên n biến  :v

Bài toán :

$f(x1+x2+...+xn) -f(x1x2...xn) =\sum  f(x1) -f(x1)f(x2)...f(xn)$

Để giải bài toán này

Ta phải xét trường hợp n =2 ( lời giải như bài MO)

Lý luận tương tự $\Rightarrow f(0)= 0$ khi cho tất cả các biến $=0$

Sau đó cho $x3 ,...xn =0 \Rightarrow f(x1+x2)=f(x1) +f(x2) .$

Từ đó suy ra f cộng tính sau đó suy ra f nhân tính

$\Rightarrow$ f đồng biến.

Và phần còn lại giải như TH n=2

 

Bài làm :

Thay $y=0$ ta có $f(x) +f(0) =f(x) -f(0) +f(x).f(0) \Rightarrow 2f(0) =f(x).f(0) \forall x \in R  (1)$

Thay $x=y=0$ ta có : $2f(0) =f^2(0)$

Xét $f(0) \neq 0$ thay vào $(1)$ ta có $f(x) =2 \forall x \in R$

Xét $f(0) =0$

Từ $(*)$  thay $x=y=1 \Rightarrow f(1)=f^2(1)$

Xét $f(1) =1$

Từ $(*)$ ta thay $y=1 \Rightarrow f(x-1) +f(x) =f(x) -1 +f(x) \forall x \in R$

$\Rightarrow f(x) -f(x-1) =1 \forall x \in R$

$\Rightarrow f(x-1) -f(x-2) =1 \forall x \in R$

Tương tự đến $f(x-(x-2)) -f(x-(x-1)) =1 \forall x \in R$

Cộng lại ta có $f(x) -f(1) =x-1 \forall x \in R$

$\Rightarrow f(x)=x \forall x \in R$

Xét $f(1) =0$

Thay $y=1 \Rightarrow f(x-1) +f(x) =f(x) \Rightarrow f(x-1) =0 \forall x \in R$

\Rightarrow f(x) =0 \forall x \in R$

Thử lại thấy đúng.

Vậy $f(x) =f(1)x \forall x \in R$

hoặc $f(x) =2$ nếu $f(0) \neq 0$

 

Bài làm

-------------

p/s Bài làm e viết lộn 1 tí ở phần bunia :3 , em sửa thành  $\frac{(x+y+z+1)^2}{3} =\frac{210^2}{3}$ . Em rất xin lỗi về sự nhầm lẫn trên

Bài Làm :
Gọi A là thành phố có nhiều đường đi +đường đi đến nhất 

Gọi tập các thành phố có đường đi từ A đến là X . Có x phần tử

Gọi tập các thành phố đi đến A là Y .Có y phần tử

Gọi tập các thành phố không đến cũng không đi đến A là Z . Có z phần tử.

Khi đó $x+y+z =209$

Nếu tồn tại 1 đường đi trong tập X thì vô lý

Nếu tồn tại 1 đường đi trong tập Y cũng vô lý

Do A là thành phố có nhiều đường đi và đi đến nhất nên x+y >x+z và x+y >y+z

Nên để có nhiều đường đến nhất thì các thành phố ở Z liên kết với các thành phố ở X,Y 

Vậy Số các đường đi liên quan đến Z không quá z(x+y)

Các đường đi giữa X,Y là xy

Vậy tổng số đường đi là  $xy+ z(x+y) +x+y  =yx +x(z+1) +(z+1)y \leq (x+y+z+1)^2 =\frac{210^3}{3}$ ( theo bunia )

Dấu = xảy ra khi x=y=z+1 Khi A đi đến 70 thành phố  , và bị 70 thành phố khác đi đến . Các thành phố đi đến và bị đi đến A đều đi đến và bị đến 69 thành phố còn lại

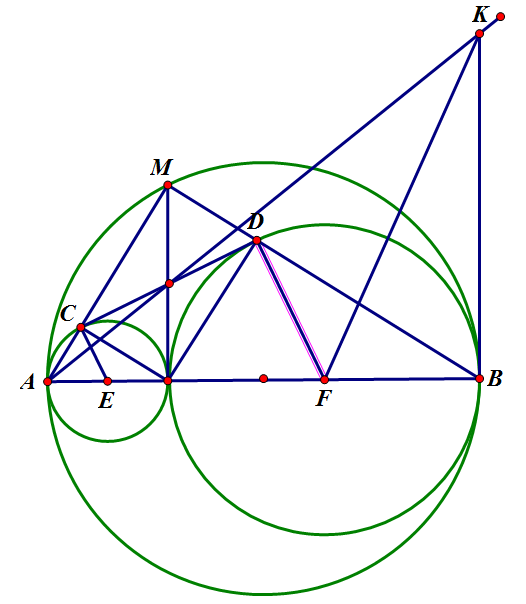
Bài làm :

Chọn trục tọa độ có $Ox \equiv d$

Đặt $A (a_x ,a_y) ,B(b_x ,b_y) ,C(c_x,c_y) ,M(m,0) ,U(u,0) ,V(v,0)$

Ta có $\frac{MR}{MU} =\frac{MS}{MV} =k$

Vậy $x_{R} =m-(m-u)k=m(1-k) +uk$

Tương tự $x_S =m(1-k) +vk$

Vậy $R (m(1-k)+uk ,0) và S (m(1-k)+vk ,0)$

Phương trình đường thẳng AB là $\frac{x-a_x}{b_x-a_x} =\frac{y-a_y}{b_y -a_y}$

$\Leftrightarrow \frac{(x-a_x)(b_y-a_y) +a_y(b_x-a_x)}{b_x-a_x} =y$

Như vậy P là  giao điểm của  $x =m(1-k) +uk$ và AB 

$\Rightarrow y_p =\frac{(m(1-k)+uk-a_x)(b_y -a_y)}{b_x-a_x} +a_y $

Vậy $P (m(1-k)+uk ,\frac{(m(1-k) +uk -a_x)(b_y -a_y)}{b_x -a_x} +a_y)$

Chứng minh tương tự ta cũng có

$Q (m(1-k) +vk ,\frac{(m(1-k) +vk -a_x)(c_y-a_y)}{c_x -a_x} +a_y)$

Vậy $\vec{PQ} = (k(v-u) ,\frac{(m(1-k)+uk -a_x)(c_y -a_y)}{c_x -a_x} -\frac{(m(1-k) +vk -a_x)(b_y-a_y)}{b_x-a_x})$

Phương trình đường thẳng từ M vuông góc PQ là :

$k(v-u) (x-m) +(\frac{(m(1-k) +uk -a_x)(c_y-a_y)}{c_x-a_x}-\frac{(m(1-k)+vk -a_x)(b_y-a_y)}{b_x -a_x})y =0$

Gọi phương trình trên là P(x,y)

Giả sử đường thẳng qua M vuông góc PQ đi qua điểm cố định $T (x_0 ,y_0)$

Thì $P (x_0 ,y_0) =0 \forall m$ 

Đây là phương trình bậc 1 đối với m nên P(x_0 ,y_0) =0 $\forall m$ $\Leftrightarrow $mọi hệ số =0

Ta có hệ số $m = -k(v-u) +(1-k)(\frac{c_y-a_y}{c_x-a_x} -\frac{b_y-a_y}{b_x-a_x})y_o=0$

Nếu $ \frac{c_y -a_y}{c_x-a_x} -\frac{b_y-a_y}{b_x-a_x} =0$

$\Leftrightarrow \frac{c_y}{v-a_x} =\frac{b_y}{u-a_x}$ ( Do $a_y=0 ,b_x =y ,c_x=v$)

$\Leftrightarrow \frac{CV}{VA} =\frac{BU}{UA}$

$\Leftrightarrow tan_{\angle UAB} =tan_{\angle VAC} \Leftrightarrow \Delta AUB =\Delta AVC$ . Khi đó ta chọn gốc tọa độ tại A thì $u-v =0 \Rightarrow hệ số m =0$ 

Nếu không , ta chọn $y_0 =\frac{k(v-u)}{(1-k)(\frac{c_y-a_y}{c_x-a_x} -\frac{b_y -a_y}{b_x-a_x})} =\frac{k(v-u)}{(1-k)(\frac{c_y}{v-a_x}-\frac{b_y}{u-a_x})} $

Hệ số bậc 0 của m là $x_0(v-u)k +y_0 ((uk-ax)\frac{c_y-a_y}{c_x-a_x}- (vk -ax)\frac{b_y-a_y}{b_x -a_x}) =0$

Nếu u=v thì ta thay vào  , hệ số bậc 0 của m cũng =0

Nếu u khác v ta chọn $x_0 =\frac{\frac{k(v-u)}{(1-k)(\frac{c_y-a_y}{c_x-a_x} -\frac{b_y-a_y}{b_x-a_x})} .((uk-ax)\frac{c_y-a_y}{c_x-a_x} -(vk-ax)\frac{b_y-a_y}{b_x-a_x})}{u-v}$

Tóm lại Đường thẳng qua M vuông góc PQ luôn đi qua điểm cố định

 

 

Lời giải khá ổn. Tuy nhiên, em nên xem xét kĩ hơn các mẫu số khi thực hiện kiểu tọa độ này.

$d=8,5$

$d_{mr}=0;d_{t}=0;d_{tl}=0$

$S=40,5$

Đề của trọng tài:

Bài 1: Cho $49c\ge a\ge b\ge c>0$. Chứng minh:
$$a+4b+7c\le 4\left( \sqrt{ab}+\sqrt{bc}+\sqrt{ca} \right)$$

Bài 2: Cho các số không âm $x,y$. Chứng minh:
$$\frac{{{x}^{4}}+{{y}^{4}}}{{{\left( x+y \right)}^{4}}}+\frac{\sqrt{xy}}{x+y}\ge \frac{5}{8}$$


Chú ý: Chỉ cần giải 1 trong 2 bài.
Không sử dụng các phương pháp vượt quá chương trình THCS.
Thời gian làm bài được tính từ 12 giờ ngày 4 tháng 6 năm 2012.

Ta xét y = 0 $\rightarrow$ Bất đẳng thức cần chứng minh $\leftrightarrow$ 1+0=1 $\geq \frac{5}{8}$( luôn đúng)
Ta xét x = 0 $\rightarrow$ Bất đẳng thức cần chứng minh $\leftrightarrow$ 1+0=1 $\geq \frac{5}{8}$( luôn đúng)
Khi y $\neq$ 0 , ta đặt $\sqrt{\frac{x}{y}}$ =a (a > 0)

Bất đẳng thức cần chứng minh:
$\leftrightarrow \frac{\frac{x^4 + y^4}{y^4}}{\frac{(x+y)^4}{y^4}} +\frac{\sqrt{xy}}{\frac{x}{y} +1} \ge \frac{5}{8}$
$\leftrightarrow \frac{a^8 +1}{(a^2+1)^4} +\frac{a}{a^2 +1} \ge \frac{5}{8}$
$\leftrightarrow \frac{a^8 +1}{(a^2+1)^4} +\frac{a(a^2 +1)^3}{(a^2 +1)^4} \ge \frac{5}{8}$
$\leftrightarrow \frac{a^8 +1 +a(a^2 +1)^3}{a^2 +1)^4}\ge \frac{5}{8}$
Quy đồng lên ta có :
$\leftrightarrow 8(a^8 +1 +a(a^2 +1)^3) \geq 5(a^2 +1)^4 $
$\leftrightarrow 8(a^8 +1+a^7 +3a^5 +3a^3 +a ) \geq 5(a^8 +4a^6 +6a^4 +4a^2 +1)$
$\leftrightarrow 8(a^8 +1+a^7 +3a^5 +3a^3 +a ) - 5(a^8 +4a^6 +6a^4 +4a^2 +1) \geq 0$
$\leftrightarrow 3a^8 + 8a^7 -20a^6 +24a^5 -30a^4 +24a^3 -20a^2 +8a +3 \geq 0$
$\leftrightarrow (3a^8 -3a^7) +(11a^7 -11a^6) -(9a^6 -9a^5)+(15a^5 -15a^4)-(15a^4 -15a^3)+(9a^3 -9a^2)-(11a^2 -11a^1)-3(a-1)\geq 0$
$\leftrightarrow (a-1)(3a^7 +11a^6 -9a^5 +15a^4 -15a^3 +9a^2 -11a -3) \geq 0$
$\leftrightarrow (a-1)[(3a^7 -3a^6) +(14a^6 -14a^5)+(5a^5 -5a^4)+(20a^4 -20a^3)+ (5a^3 -5a^2)+(14a^2 - 14a^1)+3(a-1)] \geq 0$
$\leftrightarrow (a-1)^2 (3a^6 +14a^5 +5a^4 +20a^3 +5a^2 +14a +3) \geq 0$
Ta có $(a-1)^2 \geq 0 $
$a>0 \Rightarrow 3a^6 +14a^5 +5a^4 +20a^3 +5a^2 +14a +3 \geq 0$
Do đó $\rightarrow$ ĐPCM ,dấu "=" sảy ra $\leftrightarrow a=1 \leftrightarrow \sqrt\frac{x}{y} =1 \leftrightarrow x=y$ $\leftrightarrow Q.E.D$

D-B=27.5h
E=10
F=0
S=50.5

Đặt $a =\frac{1}{x} ,b =\frac{1}{y} ,c =\frac{1}{z}$

Thay vào điều kiện ta có a+b+c=3

Thay vào bất đẳng thức . Ta cần chứng minh $\sum \frac{ab}{(a^2+b^2)(1+ab)}  \leq \frac{3}{4}$

$\sum \frac{ab}{(a^2+b^2)(1+ab)} =\sum \frac{ab}{ab(a^2+b^2) +a^2+b^2} \leq \sum \frac{ab}{ab(a^2+b^2+2)} =\sum \frac{1}{a^2+b^2+2}$

Ta sẽ chứng minh $\sum \frac{1}{a^2+b^2+2} \leq \frac{3}{4}$

$\Leftrightarrow \sum \frac{a^2+b^2}{a^2+b^2 +2} \geq \frac{3}{2}$

Mà $\sum \frac{a^2+b^2}{a^2+b^2 +2} \geq \frac{ (\sum \sqrt{a^2+b^2})^2}{2(a^2+b^2+c^2)+6}$

Ta sẽ chứng minh

$\frac{ (\sum \sqrt{a^2+b^2})^2}{2(a^2+b^2+c^2)+6} \geq \frac{3}{2}$

$\Leftrightarrow (\sum \sqrt{a^2+b^2})^2 \geq 3(a^2+b^2+c^2) +18$

$\Leftrightarrow 2\sqrt{a^2+b^2}\sqrt{b^2+c^2} +2 \sqrt{b^2+c^2}\sqrt{c^2+a^2} +2\sqrt{c^2+a^2}\sqrt{a^2+b^2} \geq a^2+b^2+c^2 +18$

Mà $2\sqrt{a^2+b^2}\sqrt{b^2+c^2} +2 \sqrt{b^2+c^2}\sqrt{c^2+a^2} +2\sqrt{c^2+a^2}\sqrt{a^2+b^2} \geq \sum 2(b^2 +ac)=(a+b+c)^2 +a^2+b^2+c^2 \geq 18 +a^2+b^2+c^2 .$

Như vậy ta có dpcm 

Vậy BĐT cần chứng minh đúng .Dấu = xảy ra khi x=y=z =1

Bài làm :

Nếu $y =0 \Rightarrow x=1$

Nếu $y \geq 1$. Ta có $x > y$

Mặt khác $x^2 =y^2 +\sqrt{y+1} < y^2 +2y +1 =(y+1)^2$ ( Do $y+1 <(2y+1)^2 \forall y \geq 1$ )

$\Rightarrow y^2 < x^2  < (y+1)^2$ . Khi đó phương trình vô nghiệm.

Vậy nghiệm của phương trình là $(x,y) =(1,0)$

 

Không thử lại: trừ 1đ

$d=9$

$d_{mr}=0; d_{t}=0; d_{tl}=0$

$S=44$

Chứng minh bằng phương pháp phản chứng . Gọi các hình chữ nhật nhỏ là : $A_{1} ,A_{2} , A_{3},A_{4} ...... A_{9}$
giả sử diện tích các phần chung của 2 hình chữ nhật nào cũng nhỏ hơn $\frac{1}{9}$
$A_{1}$ có diện tích =1
Phần diện tích của$A_{2}$ không bị phủ bởi $A_{1}$ luôn lớn hơn :
1 - $\frac{1}{9}$=$\frac{8}{9}$
Phần diện tích của $A_{3}$ không bị phủ bởi $A_{1}$ và $A_{2}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} = \frac{7}{9}$

Phần diện tích của $A_{4}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} = \frac{6}{9}$

Phần diện tích của $A_{5}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ và $A_{4}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} = \frac{5}{9}$

Phần diện tích của $A_{6}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ và $A_{4}$ và $A_{5}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} = \frac{4}{9}$

Phần diện tích của $A_{7}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ và $A_{4}$ và $A_{5}$và $A_{6}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9}= \frac{3}{9}$

Phần diện tích của $A_{8}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ và $A_{4}$ và $A_{5}$và $A_{6}$ và $A_{7}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9}= \frac{2}{9}$

Phần diện tích của $A_{9}$ không bị phủ bởi $A_{1}$ và $A_{2}$ và $A_{3}$ và $A_{4}$ và $A_{5}$và $A_{6}$ và $A_{7}$ và $A_{8}$ luôn lớn hơn :
1-$\frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} - \frac{1}{9} = \frac{1}{9}$
Tổng diện tích của 9 hình chữ nhật sẽ lớn hơn:
$\frac{8}{9}+\frac{7}{9}+\frac{6}{9}+\frac{5}{9}+\frac{4}{9}+\frac{3}{9}+\frac{2}{9}+\frac{1}{9}=5 $
Điều nè vô lý

Bài này dễ:
Cho xy cắt AB ở K,AC ở H.
Ta có :
$\frac{BB'}{AA'}=\frac{BK}{AK},\frac{CC'}{AA'}=\frac{CH}{AH}\Rightarrow \frac{BB'+CC'}{AA'}=\frac{BK}{AK}+\frac{CH}{AH}=\frac{AB}{AK}-1+\frac{CH}{AH}-1=\frac{AB}{AK}+\frac{CH}{AH}-2$
Từ B,C vẽ BJ,CI // xy (I,J thuộc AG) .Cho BC cắt AG tại M => MB=MC
=> MI=MJ
Vậy ta có $\frac{BB'+CC'}{AA'}=\frac{AB}{AK}+\frac{CH}{AH}-2=\frac{AJ+AI}{AG}-2=\frac{2AI+IJ}{AG}-2=\frac{2AI+2IM}{AG}-2=\frac{2AM}{\frac{2}{3}AM}-2=3-2=1\Rightarrow AA'=BB'+CC'(Q.E.D)$
Đây là hình vẽ

sao anh chém tởm vậy
Cách khác:
kẻ $ MI \perp B'C'$
$\rightarrow MI =\frac{BB' +CC"}{2}$
Dễ thấy$ \Delta AA'G$ ~ $\Delta MIG$
$\rightarrow \frac{AA'}{MI} =2$
$\rightarrow AA' =BB' +CC'$
_________________
@Mod: học đâu cái kiểu chửi cách làm người ta rồi khi bị phản bác lại đổi đen thành trắng thế ?
Chú ý cách ăn nói
Cảnh cáo lần 1 /!\