Mấy ông ơi !!
Up cái này phát!
Ông quả nhìn to quá!
cái bảng đó bây h ai giữ thế ;p
Bữa nào bán đấu giá trên Vmf đi
Có 85 mục bởi Stranger411 (Tìm giới hạn từ 30-04-2020)
 Đã gửi bởi
Stranger411
on 11-08-2012 - 14:58
trong
Góc giao lưu
Đã gửi bởi
Stranger411
on 11-08-2012 - 14:58
trong
Góc giao lưu
Mấy ông ơi !!
Up cái này phát!
Ông quả nhìn to quá!
 Đã gửi bởi
Stranger411
on 29-06-2013 - 11:02
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 29-06-2013 - 11:02
trong
Tổ hợp và rời rạc
Bài 2: (PP ánh xạ, chứng minh đặc tính tổ hợp) Gọi an là số các xâu nhị phân độ dài n không chứa chuỗi con 010, bn là số các xâu nhị phân độ dài n không chứa chuỗi con 0011 hoặc 1100. Chứng minh rằng bn+1 = 2an với mọi n nguyên dương.
Giải bài 2:
Xét một xâu nhị phân bất kì $\left \{ x_1, x_2,...,x_n \right \}$.
Ta xây dựng một xâu nhị phân $\left \{ y_1, y_2,...,y_{n+1} \right \}$ sao cho $y_1 =0$ và $y_k = x_1 + x_2 +...+ x_k(mod2)$
Rõ ràng, xâu $\left \{ x_1, x_2,...,x_n \right \}$ có dạng $a_n$ khi và chỉ khi $\left \{ y_1, y_2,...,y_{n+1} \right \}$ có dạng $b_n$. Nói cách khác đó là một song ánh biến các xâu có dạng $a_n$ thành các xâu có dạng $b_{n+1}$ bắt đầu bằng $0$.
Với mỗi xâu $\left \{ y_1, y_2,...,y_{n+1} \right \}$, ta thay các kí tự 1 bởi 0 và 0 bởi 1, ta được một xâu khác cũng có dạng $b_{n+1}$ nhưng bắt đầu bởi $1$.
Từ đó cho ta: $b_{n+1} = 2a_n$.
Bài 3 (Toán trò chơi-Nguồn: Tournament of the Towns). Trên bảng ô vuông $20$x$20$ mỗi ô có $1$ quân cờ. $A$ chọn một số thực $d$ và $B$ phải đưa mỗi quân cờ đi tới ô cách ô ban đầu nó đứng một khoảng cách ít nhất là $d$ (khoảng cách giữa $2$ ô được tính theo khoảng cách tâm của $2$ ô đó) và mỗi ô chỉ có thể có $1$ quân cờ. Hỏi với điều kiện gì của $d$ thì $B$ có thể thao tác thoả mãn điều kiện trên?Hỏi tương tự với bảng $21$x$21$
Với bài này có lẽ ta phải chia bàn cờ ra 4 phần.
Cái đáp số hơi lằng nhằng, không biết có đúng không.
 Đã gửi bởi
Stranger411
on 30-06-2013 - 22:38
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 30-06-2013 - 22:38
trong
Tổ hợp và rời rạc
Bài 11:(Lý thuyết đồ thị, APMO 1989) Chứng minh rằng một đồ thị n đỉnh, k cạnh thì sẽ có ít nhất $\frac{{k\left( {4k - {n^2}} \right)}}{{3n}}$ tam giác.
Câu này được chế biến lại làm đề chọn đội tuyển của KHTN năm nào đó thì phải, nhưng cũng chỉ là điều kiện cần.
Giải bài 11:
Gọi $D_i$ là bậc của đỉnh $i$ nào đó.
Nếu 2 đỉnh $i$ và $j$ liên thông thì tồn tại ít nhất $D_i + D_j - 2$ cạnh khác nổi đến $n-2$ đỉnh khác của đồ thị.
Nên có $D_i + D_j - n$ tam giác có đỉnh là $j$ và $j$. Vậy số tam giác có chứa cạnh $ij$ được tạo thành phải tối thiểu là:
$\sum_{i,j} {\frac{D_i + D_j -n}{3}}=\sum_{i,j} {\frac{D_i + D_j}{3} - \frac{nk}{3}} = \sum_{i} {\frac{D_i^2}{3} - \frac{nk}{3}}$
Vậy số tam giác tối thiểu được tạo thành là:
$\sum_{i}{\frac{D_i^2}{3}} -\frac{nk}{3} \geq \frac{1}{3n}\left ( \sum_{i}{D_i} \right )^2 - \frac{nk}{3} = \frac{4k^2}{3n} -\frac{nk}{3}$
Q.E.D.
Bài 6: (truy hồi/đa thức,giải tích tổ hợp,PTNK 2009) Cho số nguyên dương n. Có bao nhiêu số chia hết cho 3, có n chữ số và các chữ số đều thuộc {3, 4, 5, 6}?
Sau đây là cách giải PP truy hồi:
Gọi $a_n$ là số các số có $n$ chữ số lập từ ${3, 4, 5, 6}$ và chia hết cho 3, còn $b_n$ là số các số có $n$ chữ số lập từ ${3, 4, 5, 6}$ và không chia hết cho 3. Khi đó ta có
$a_n = 2a_{n-1} + b_{n-1}(1)$
$b_n = 2a_{n-1} + 3b_{n-1}(2)$
Từ (1) suy ra $b_{n-1} = a_n – 2a_{n-1}$, thay n à n+1 thì được $b_n = a_{n+1} – 2a_n$. Thay vào (2), ta được
$a_{n+1} – 2a_n = 2a_{n-1} + 3(a_n – 2a_{n-1})$
$a_{n+1} – 5a_n + 4a_{n-1} = 0$.
Giải phương trình sai phân này, với chú ý rằng a1 = 2, a2 = 6, ta tìm được
\[{a_n} = \frac{{{4^n} + 2}}{3}.\]
Với cách đặt trên ta có thể có công thức truy hồi khác là $b_n = 4^n - a_n$
từ đó suy ra $a_{n+1} = 2a_{n} + b_{n}= a_n + 4^n$
Nên $a_{n} = 4^{n-1} + 4^{n-2} +...+ a_{1} = \frac{4^n + 2}{3}$
 Đã gửi bởi
Stranger411
on 03-07-2013 - 10:00
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 03-07-2013 - 10:00
trong
Tổ hợp và rời rạc
Bài 17 (cực trị-bất đẳng thức tổ hợp)
Cho tập hợp $X=\left \{ 1,2,...,50 \right \}$. Tìm số nguyên dương nhỏ nhất $k$ sao cho mọi tập con gồm $k$ phần tử của $X$ đều chứa hai phần tử phân biệt $a$ và $b$ sao cho $ab$ chia hết cho $a+b$
Ta có các cặp số thoả mãn $ab$ chia hết $a+b$: $(3;6);(4;12);(5;20);(6;12);(6;30);(7;42);(8;2);(9;18);(10;15);(10;40);(12;24);(12;36);(14;35);(15;30);(16;48);(18;36);(20;30);(21;28);(21;42);(24;40);(24;48);(30;45);(36;45)$
Tổng hợp các số lại tập $A$, ta có:\[A = \left\{ {3;4;5;6;7;8;9;10;12;14;15;16;18;20;21;24;30;35;36;40;45;48} \right\}\]
\[ \Rightarrow k \ge \left| {X\backslash A} \right| + \left[ {\frac{{\left| A \right|}}{2}} \right] + 1 = 39\]
Vậy $min(k)=39$
--------------------------------------------------------------------------------------------------------------------------------
Đây là kết quả sau 1h bấm máy tính của mình, các bạn có cách nào hay hơn thì đưa lên để mọi người cùng tham khảo
Giải bài 17:
Chứng minh $k \ge 39$
Các cặp số thoả mãn $ab$ chia hết $a+b$: $(3;6);(4;12);(5;20);(6;12);(6;30);(7;42);(8;2);(9;18);(10;15);(10;40);(12;24);(12;36);(14;35);(15;30);(16;48);(18;36);(20;30);(21;28);(21;42);(24;40);(24;48);(30;45);(36;45)$
Xét tập $M=(6,12,15,18,20,21,24,35,40,42,45,48)$. Vì 23 cặp trên đều có phần tử thuộc $M$ nên tập $X\M$ không thỏa mãn bài toán. Mà $|X\M|=38 \rightarrow k \ge 39$
Chứng minh mọi tập có 39 phần tử đều thỏa mãn bài toán:
Xét tập $A$ bất kì gồm 39 phần tử của $X$.
Chọn 12 cặp số trong 23 cặp trên sao cho các phần tử không trùng nhau: $(3;6);(4;12);(5;20);(7;42);(8;2);(9;18);(10;15);(14;35);(18;36);(21;28);(24;40);(30;45)$
12 cặp trên chứa 24 phần tử của $X$. Nên $X$ chỉ còn lại 26 phần tử.
Vậy ít nhất 13 phần tử của $A$ của phải thuộc 12 cặp trên.
Theo nguyên lí drichlet thì $A$ chứa ít nhất 1 trong 12 cặp trên.
Từ đó tập $A$ thỏa mãn đề bài.
 Đã gửi bởi
Stranger411
on 02-07-2013 - 12:05
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 02-07-2013 - 12:05
trong
Tổ hợp và rời rạc
Post tiếp 2 bài nữa làm ... điểm tâm
:
Bài 15:(APMO 1998) Cho F là tập tất cả các bộ (A1, . . . ,An) sao cho mỗi Ai là một tập con của {1, 2, . . . , 1998}. Ký hiệu |A| là số các phần tử của tập hợp A. Hãy tính
$\sum\limits_{({A_1},{A_2},...,{A_n}) \in F} {|{A_1} \cup {A_2} \cup ... \cup {A_n}|} $
Bài 16:(Bulgaria 1996) HÌnh chữ nhật $m \times n ( m,n \in N, m,n>1)$ được chia thành $mn$ hình vuông đơn vị. Có bao nhiêu cách xoá 2 hình vuông sao cho phần còn lại có thể lát kín bởi các domino?
Tại sao các bạn cứ thích post những bài không có lời giải ở trong sách ra thế nhỉ ![]()
Mình nhớ không nhầm thì mấy bài này trong chuyên đề của thầy Huỳnh Tấn Châu để học sinh tự giải. Sau đây là cách của mình, bạn có cách khác thì post lên cho mọi người tham khảo.
Giải bài 15:
Bài này đếm bằng truy hồi.
Tập $(1, 2, . . . , 1998)$ có tất cả $2^{1998}$ tập con $A_i$ nên tổng cần tính có tất cả $2^{1998n}$ bộ $n$ số.
Bước 1: Với các tập con $(A_1, A_2 ... , A_n)$ của $(1, 2, . . . , 1997)$, ta có thể thêm hoặc không thêm vào mỗi tập $A_i$ phần tử $1998$ để tạo thành tập con của tập $(1, 2, . . . , 1998)$. Vậy từ bộ $(A_1, A_2 ... , A_n)$ ta có $2^n$ bộ gồm các tập con của $\left \{1, 2, . . . , 1998 \right \}$.
Bước 2: Bây h chỉ còn xét các tập con $(A_1, A_2 ... , A_n)$ của các bộ còn lại. Làm tương tự như trên thì ta có được $(2^n -1).2^{n(m-1)}$.
Tình tổng lại, ta có:
$\sum\limits_{({A_1},{A_2},...,{A_n}) \in (1,...,1998)} {|{A_1} \cup {A_2} \cup ... \cup {A_n}|} = (2^n.\sum\limits_{({A_1},{A_2},...,{A_n}) \in (1,...,1998)} {|{A_1} \cup {A_2} \cup ... \cup {A_n}|}) + (2^n -1) 2^{n(m-1)}$
Từ đó, ta có: $\sum\limits_{({A_1},{A_2},...,{A_n}) \in F} {|{A_1} \cup {A_2} \cup ... \cup {A_n}|} = 1998(2^{1998n} - 2^{1997n})$.
Mở rộng bài 15: Tính:
$P= \sum_{(A_{1},A_{2},...,A_{k})\in F_{k}}\sum_{b\in (A_{1}\cup A_{2}\cup ...\cup A_{k})}b$
$S= \sum_{(A_{1},A_{2},...,A_{k})\in F_{k}}\sum_{i=1}^{k}\sum_{b\in A_{i}}b$
Bài 7: (Đề đề nghị 30/4 -2012) Trong một kì thi hoa hậu, mỗi thành viên của ban giám khảo được quyền đề xuất $10$ người đẹp vào vòng chung kết. Một nhóm người đẹp được gọi là nhóm ưng ý đối với giám khảo A nếu trong nhóm đó có ít nhất một người đẹp mà A đề xuất. Biết rằng với 6 giám khảo bất kỳ luôn tồn tại một nhóm gồm 2 người đẹp là nhóm ưng ý đối với mỗi giám khảo trong 6 giám khảo đó. Chứng minh rằng tồn tại một nhóm gồm 10 người đẹp là nhóm ưng ý đối với mỗi thành viên của ban giám khảo.
Đề này của trường chuyên Nguyễn Tất Thành - Komtum và họ không đưa đáp án nên trong sách không có lời giải.
Mình nghĩ bạn Ispectorgadget cũng không có đáp án cho bài này. (Trừ khi bạn ấy học trường chuyên NTT)
Bài này chắc không thể giải bằng đồ thị vì phải xét tới 2 đối tượng là hoa hậu và giám khảo.
Thôi thì phát biểu lại dưới dạng tập hợp để mọi người cùng nghiên cứu:
Cho $X=\{1;2;...;n\}$. Và $A_1 ,A_2, ..., A_m$ là các tập con của $X$.
Biết 6 phần tử bất kì của $X$ luôn thuộc $|A_i\cup A_j|$ nào đó.
Chứng minh tồn tại $i_1;i_2;..;i_{10}$ phân biệt mà $|\bigcup\limits_{j=1}^{10}A_{i_j}|=X$.
 Đã gửi bởi
Stranger411
on 13-08-2012 - 09:42
trong
Góc giao lưu
Đã gửi bởi
Stranger411
on 13-08-2012 - 09:42
trong
Góc giao lưu
Ố ố :-ssDuyệt cho anh =))
 Đã gửi bởi
Stranger411
on 24-04-2012 - 19:32
trong
Bất đẳng thức - Cực trị
Đã gửi bởi
Stranger411
on 24-04-2012 - 19:32
trong
Bất đẳng thức - Cực trị
Bài này khá yếu.Problem 8: Cho a,b,c là các số thực thỏa $a+b+c=3$. Chứng minh rằng:
$$\frac{a^2-bc}{a^2+3}+\frac{b^2-ac}{b^2+3}+\frac{c^2-ab}{c^2+3}\geq 0$$
 Đã gửi bởi
Stranger411
on 24-06-2013 - 20:42
trong
Tài liệu - Đề thi
Đã gửi bởi
Stranger411
on 24-06-2013 - 20:42
trong
Tài liệu - Đề thi
Bài 4. (1,5 điểm)
Cho một tháp số (gồm 20 ô vuông giống nhau) như hình vẽ. Mỗi ô vuông được ghi một số nguyên dương n với $1\leq n\leq 20$, hai ô vuông bất kỳ không được ghi cùng một số. Ta quy định trong tháp số này 2 ô vuông kề nhau là 2 ô vuông có chung cạnh. Hỏi có thể có cách ghi nào thỏa mãn điều kiện: Chọn 1 ô vuông bất kỳ (khác với các ô vuông được đặt tên a, b, c, d, e, f, g, h như hình vẽ) thì tổng của số được ghi trong ô đó và các số được ghi trong 3 ô vuông kề với nó chia hết cho 4 ?

 Đã gửi bởi
Stranger411
on 09-08-2013 - 15:20
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
Stranger411
on 09-08-2013 - 15:20
trong
Thi HSG Quốc gia và Quốc tế
Mới có bản Scan thôi, các bạn dùng tạm ![]()
 VNMATH.COM-imo 2012 shortlist.pdf 615.93K
1984 Số lần tải
VNMATH.COM-imo 2012 shortlist.pdf 615.93K
1984 Số lần tải
 Đã gửi bởi
Stranger411
on 09-11-2012 - 21:48
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 09-11-2012 - 21:48
trong
Tổ hợp và rời rạc
Chào các anh. Bài này dùng hàm sinh kết hợp với RUF tức là Root of Unity Filter đó ạDạo này box tổ hợp và rời rạc của VMF có vẻ trầm lắng!
Để tránh tình trạng này kéo dài, tôi xin khuấy động bằng một bài nho nhỏ
Cho số nguyên $n\ge 3$. Chứng minh đẳng thức:
$\sum_{k=0}^{\left\lfloor\frac{n}{3}\right\rfloor} \binom{n}{3k} = \dfrac{2^n+(-1)^n\left(3\left\lfloor\frac{n}{3}\right\rfloor-3\left\lfloor\frac{n-1}{3}\right\rfloor-1\right)}{3}$
 Đã gửi bởi
Stranger411
on 01-06-2013 - 16:36
trong
Hình học
Đã gửi bởi
Stranger411
on 01-06-2013 - 16:36
trong
Hình học
Bài toán khá hay đó bạn:
Qua $M$ vẽ đường thẳng song song với $d$,Cắt $(O)$ tại $N$,cắt $OH$ tại $I$.
Vì $HA=HB$ và $MN//AB$ nên $M(AB,HN)=-1$,Chiếu chùm điều hòa lên $(O)$ ta có tứ giác $DCEN$
Kí hiệu mà bạn dùng chỗ nào là thế nào vậy ?
mình xem lại lí thuyết về chùm điều hòa mà không thấy.
 Đã gửi bởi
Stranger411
on 01-06-2013 - 15:17
trong
Hình học
Đã gửi bởi
Stranger411
on 01-06-2013 - 15:17
trong
Hình học
Cho đường tròn $(O)$ và đường thẳng $d$. Gọi $H$ là hình chiếu của $O$ lên $d$. Cho 2 điểm $A,B \in d$ sao cho $HA =HB$. Lấy $M$ bất kì trên $(O)$. $MH,MA,MB$ lần lượt cắt $(O)$ tại $C,D,E$. Gọi $S$ là giao điểm của d và $DE$. Chứng minh $SC$ là tiếp tuyến của đường tròn $(O)$.
 Đã gửi bởi
Stranger411
on 01-06-2013 - 17:28
trong
Hình học
Đã gửi bởi
Stranger411
on 01-06-2013 - 17:28
trong
Hình học
Qua $M$ vẽ đường thẳng song song với $d$,Cắt $(O)$ tại $N$,cắt $OH$ tại $I$.
Vì $HA=HB$ và $MN//AB$ nên $M(AB,HN)=-1$
Theo mình thấy chỗ này nên chứng minh lại bổ đề sau:
Bổ đề 1: Cho $a,b,c,d$ là chùm đường thẳng tâm $O$. Đường thẳng $\delta$ không đi qua $O$, cắt $a,b,c,d$ tại $A,B,C,D$. Đường thẳng $\delta'$ không đi qua $O$, cắt $a,b,c$ tại $A',B',C'$. Khi đó $\delta' // d$ thì $(ABCD)=(A'B'C')$.
Áp dụng bổ đề trên thì $M(ABHN)= (ABH) = -1$.
 Đã gửi bởi
Stranger411
on 11-01-2013 - 23:00
trong
Phương trình - Hệ phương trình - Bất phương trình
Đã gửi bởi
Stranger411
on 11-01-2013 - 23:00
trong
Phương trình - Hệ phương trình - Bất phương trình
 Đã gửi bởi
Stranger411
on 08-08-2013 - 14:40
trong
Hình học
Đã gửi bởi
Stranger411
on 08-08-2013 - 14:40
trong
Hình học
1 bài mở rộng của thầy Quang Hùng trong GGTH lần 5
Cho tam giác $ABC$, đường tròn $(I)$ đi qua $B,C$ cắt CA,AB tại $N,M$ khác $B,C$.
Đặt $H = BN \cap CM$. Gọi $d$ là đường thẳng qua $I$ vuông góc với $AH$. Lấy $W$ bất kì trên $d$.
$WK,WL$ là đường kính của đường tròn ngoại tiếp các tam giác $WBM,WCN$.
Chứng minh $K,H,L$ thẳng hàng.

 Đã gửi bởi
Stranger411
on 27-07-2013 - 13:22
trong
Hình học
Đã gửi bởi
Stranger411
on 27-07-2013 - 13:22
trong
Hình học
Cho tứ giác toàn phần $ABCDEF$. Chứng minh các đường tròn đướng kính $AC,BD,EF$ đồng quy tại 2 điểm.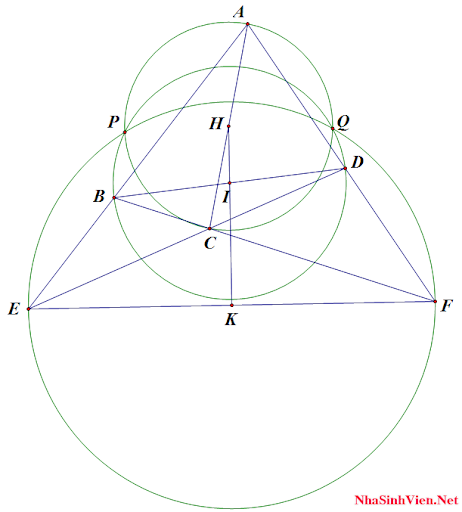
 Đã gửi bởi
Stranger411
on 11-08-2012 - 23:47
trong
Số học
Đã gửi bởi
Stranger411
on 11-08-2012 - 23:47
trong
Số học
Em Tạ giải kinh quáHe he áp dụng cái bổ đề anh Tường nói thì bài này làm ngon
Giải như sau:
Bổ đề: $p \in \mathbb{P}, p \equiv 2 \pmod{3}, a^2+3b^2 \vdots p \Leftrightarrow p|a,b$
 Đã gửi bởi
Stranger411
on 13-08-2012 - 09:49
trong
Số học
Đã gửi bởi
Stranger411
on 13-08-2012 - 09:49
trong
Số học
Gì nữa đây bạnmuốn có -3 là thặng dư toàn phương của p thì 1 trong 2 số 2a+b hoặc b không chia hết cho p,nên theo nguyenta a,b,c chia hết cho p là hợp lí
 Đã gửi bởi
Stranger411
on 13-08-2012 - 12:03
trong
Số học
Đã gửi bởi
Stranger411
on 13-08-2012 - 12:03
trong
Số học
Trước khi nói cái gì thì nên coi lại kiến thức của mình một tí đi nháý m` là không có cách của bạn đâu,nếu 2a+b chia hết cho p thì làm quoái j` mà vô lí chứ,cũng giống như a mũ 2 + b mũ 2 có ước nguyên tố dạng thì 4p+3 thì a,b cùng chia hết cho SNT đó,làm j` có chuyện vô lí ở đâu,khi sử dụng kí hiêu lengdre ta đã ngầm hiểu tử số của nó không chia hết cho mẫu r`
 Đã gửi bởi
Stranger411
on 16-08-2012 - 10:37
trong
Số học
Đã gửi bởi
Stranger411
on 16-08-2012 - 10:37
trong
Số học
Nói chuyện vs Uyenha cực kì bực mình @@!sai từ chỗ này và nguyên nhân là do làm tắt $p|{(2a + b)^2} + 3{b^2}$
$ \Rightarrow \left( {\frac{{ - 3}}{p}} \right) = 1$
muốn dùng lengdre(hay tiếng việ gọi là thặng dư toàn phương) trước tiên ta phải đưa nó về dạng (mà ở đây) là
a2$\equiv$-3 (mod p) cái đã,mà ở đây muốn đưa về dạng này ta phải giả sử a không chia hết cho p,''vậy nên thiếu TH a,b chia hết cho p'',mà TH này luôn đúng,nếu không thấy dc thì cho a=b=p ta có 12p2 chia hết cho p ,vì vậy có giải kiểu gì đi nữa vẫn phải thông qua a,b,c chia hết cho p rồi mới giải tiếp,nên không có cách bạn stranger nói
 Cong Thuc Legendre.pdf 67.83K
1682 Số lần tải
Cong Thuc Legendre.pdf 67.83K
1682 Số lần tải
 Đã gửi bởi
Stranger411
on 13-08-2012 - 21:29
trong
Số học
Đã gửi bởi
Stranger411
on 13-08-2012 - 21:29
trong
Số học
$\Rightarrow 2a^2+2ab+2b^2 \vdots p \Rightarrow 4a^2+4ab+4b^2 \vdots p \Rightarrow (2a+b)^2+3b^2 \vdots p$
Bạn xem lại @@!$c \equiv - a - b(\bmod p) \Rightarrow p|a^2 + ab + b^2 \Rightarrow p|{(2a + b)^2} + 3{b^2}$
$ \Rightarrow \left( {\frac{{ - 3}}{p}} \right) = 1$. Và điều này vô lí vì $p \equiv 2(\bmod 3)$.
Vậy không tồn tại $a,b,c$ thỏa mãn bài toán. $\blacksquare$
 Đã gửi bởi
Stranger411
on 29-04-2012 - 14:46
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
Stranger411
on 29-04-2012 - 14:46
trong
Thi HSG Quốc gia và Quốc tế
Tuy là đề thi quốc gia nhưng mình thấy bài này khá lỏngBalkan MO 2012 - 28 April 2012
Bài 2. Prove that \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] for all positive real numbers $x,y$ and $z$.
 Đã gửi bởi
Stranger411
on 04-08-2012 - 13:57
trong
Tổ hợp và rời rạc
Đã gửi bởi
Stranger411
on 04-08-2012 - 13:57
trong
Tổ hợp và rời rạc
 Đã gửi bởi
Stranger411
on 13-08-2012 - 13:46
trong
Tài liệu, chuyên đề, phương pháp về Số học
Đã gửi bởi
Stranger411
on 13-08-2012 - 13:46
trong
Tài liệu, chuyên đề, phương pháp về Số học
 Eng_v7_n4.pdf 57.08K
777 Số lần tải
Eng_v7_n4.pdf 57.08K
777 Số lần tải
 Đã gửi bởi
Stranger411
on 06-12-2012 - 00:19
trong
Số học
Đã gửi bởi
Stranger411
on 06-12-2012 - 00:19
trong
Số học
Bài này có nhiều cách giải lắm thầy ạCho $p>3$ là một số nguyên tố.
Đặt $\begin{cases}{n\over m}=\sum_{k=1}^{p-1}{1\over k}\\ \mathrm{gcd}(n,m)=1\end{cases}$
Chứng minh rằng: $p\big| n$

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học
