Chủ đề này có 5 trả lời

[thanhhuyen98]

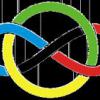
$\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\geq \frac{(x+y+z)^2}{a+b+c}$

[THYH]

$\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\geq \frac{(x+y+z)^2}{a+b+c}$

Bài toán đầy đủ là 

 

$\frac{x^{2}}{a}+\frac{y^{2}}{b}+\frac{z^{2}}{c}\geq \frac{(x+y+z)^{2}}{a+b+c}$

 

c/m:

 

ta có BĐT phụ : $\frac{x^2}{a}+\frac{y^2}{b} \geq \frac{(x+y)^{2}}{a+b}$ ( bạn có thể chứng minh bđt này bằng cách quy đồng đưa về hằng đẳng thức )

 

áp dụng 2 lần ta đc 

 $\frac{x^2}{a}+\frac{y^2}{b} +\frac{z^2}{c}\geq \frac{(x+y)^{2}}{a+b}+\frac{z^2}{c}\geq \frac{(x+y+z)^{2}}{a+b+c}$

 

 

Dấu bằng ''$a=b=c$''

 

 

p/s: đây là bđt svac-sơ vs 3 số cũng đc xem là hệ quả của B.C.S 

Bài viết đã được chỉnh sửa nội dung bởi THYH: 21-07-2013 - 16:27

[letankhang]

mà mik ngu lm p cm đi

 

$\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\geq \frac{(x+y+z)^2}{a+b+c}$

 

Áp dụng bất đẳng thức bunhiacopskia cho 3 số :

$(\sqrt{a}^{2}+\sqrt{b}^{2}+\sqrt{c}^{2})[(\frac{x}{\sqrt{a}})^{2}+\frac{y}{\sqrt{b}})^{2}+\frac{z}{\sqrt{c}})^{2}]\geq (x+y+z)^{2}$

$=>\frac{x^{2}}{a}+\frac{y^{2}}{b}+\frac{z^{2}}{c}\geq \frac{(x+y+z)^{2}}{a+b+c}$ 

$=>đpcm$

Bài viết đã được chỉnh sửa nội dung bởi letankhang: 21-07-2013 - 16:32

[hoctrocuanewton]

de bai phai la a,b,c >0 chu khong phai khong am 

Bài viết đã được chỉnh sửa nội dung bởi hoctrocuanewton: 21-07-2013 - 16:34

[Near Ryuzaki]

Sau đây là bài mình, chứng minh công thức tổng quát luôn nhé: (mấy cái a1, a2 ,...,an là dãy số nha ko phải nhân đâu)

Áp dụng bắt đẳng thức bunhiacôpski cho 2 bộ số :

$\frac{a1}{\sqrt{b1}},\frac{a2}{\sqrt{b2}},...,\frac{an}{\sqrt{bn}}$ và  $\sqrt{b1},\sqrt{b2},\sqrt{b3},....,\sqrt{bn}$

Ta có :

$(\frac{a1^{2}}{b1}+\frac{a2^{2}}{b2}+...+\frac{an^{2}}{bn})(b1+b2+b3+b4+...+bn)\geq (\frac{a1}{b1}.\sqrt{b1}+\frac{a2}{b2}.\sqrt{b2}+...+\frac{an}{bn}.\sqrt{bn}=(a1+a2+...+an)^{2}$

Từ đây suy ra điều phải chứng minh :

$\frac{a1^{2}}{b1}+\frac{a2^{2}}{b2}+...+\frac{an^{2}}{bn}\geq \frac{(a1+a2+a3+ã+...+an)^{2}}{b1+b2+b3+b4+...+bn}$

Dấu bằng xảy ra khi và chỉ khi:

$\frac{\frac{a1}{\sqrt{b1}}}{\sqrt{b1}}= \frac{\frac{a2}{}\sqrt{b2}}{\sqrt{b2}}=...= \frac{\frac{an}{\sqrt{bn}}}{\sqrt{bn}}\Leftrightarrow \frac{a1}{b1}=\frac{a2}{b2}=...=\frac{an}{bn}$

Bài viết đã được chỉnh sửa nội dung bởi sieusieu90: 21-07-2013 - 16:36

[letankhang]

Sau đây là bài mình, chứng minh công thức tổng quát luôn nhé: (mấy cái a1, a2 ,...,an là dãy số nha ko phải nhân đâu)

Áp dụng bắt đẳng thức bunhiacôpski cho 2 bộ số :

$\frac{a1}{\sqrt{b1}},\frac{a2}{\sqrt{b2}},...,\frac{an}{\sqrt{bn}}$ và  $\sqrt{b1},\sqrt{b2},\sqrt{b3},....,\sqrt{bn}$

Ta có :

$(\frac{a1^{2}}{b1}+\frac{a2^{2}}{b2}+...+\frac{an^{2}}{bn})(b1+b2+b3+b4+...+bn)\geq (\frac{a1}{b1}.\sqrt{b1}+\frac{a2}{b2}.\sqrt{b2}+...+\frac{an}{bn}.\sqrt{bn}=(a1+a2+...+an)^{2}$

Từ đây suy ra điều phải chứng minh :

$\frac{a1^{2}}{b1}+\frac{a2^{2}}{b2}+...+\frac{an^{2}}{bn}\geq \frac{(a1+a2+a3+ã+...+an)^{2}}{b1+b2+b3+b4+...+bn}$

Dấu bằng xảy ra khi và chỉ khi:

$\frac{\frac{a1}{\sqrt{b1}}}{\sqrt{b1}}= \frac{\frac{a2}{}\sqrt{b2}}{\sqrt{b2}}=...= \frac{\frac{an}{\sqrt{bn}}}{\sqrt{bn}}\Leftrightarrow \frac{a1}{b1}=\frac{a2}{b2}=...=\frac{an}{bn}$

Thiếu dấu căn ờ vài chỗ đó 

Bài viết đã được chỉnh sửa nội dung bởi letankhang: 21-07-2013 - 16:38