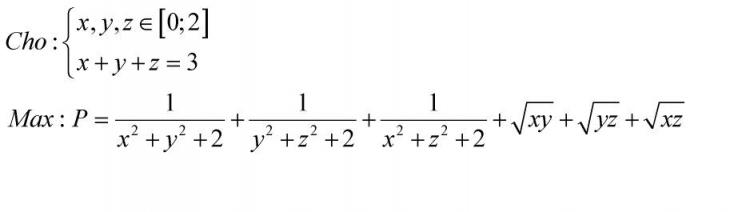$Max$ $P=\sum \frac{1}{x^{2}+y^{2}+2}+\sum \sqrt{xy}$
#1
 Đã gửi 14-01-2016 - 17:21
Đã gửi 14-01-2016 - 17:21

#2
 Đã gửi 08-06-2016 - 22:15
Đã gửi 08-06-2016 - 22:15

Ta có:
$\sum \sqrt{xy}\leq \sum x= 3$
Ta sẽ chứng minh:
$\sum \frac{1}{x^2+y^2+2}\leq \frac{3}{4}$
$\Leftrightarrow \sum \frac{x^2+y^2}{x^2+y^2+2}\geq \frac{3}{2}$
Áp dụng bất đẳng thức Cauchy-Schwarz ta có:
$\sum \frac{x^2+y^2}{x^2+y^2+2}\geq \frac{(\sum \sqrt{x^2+y^2})^2}{2(x^2+y^2+z^2)+6}= \frac{2(x^2+y^2+z^2)+2\sum \sqrt{(x^2+y^2)(y^2+z^2)}}{2(x^2+y^2+z^2)+6}$
Như vậy ta cần chứng minh:
$\frac{\sum x^2+\sum \sqrt{(x^2+y^2)(y^2+z^2)}}{.\sum x^2+3}\geq \frac{3}{2}$
$\Leftrightarrow 2\sum \sqrt{(x^2+y^2)(y^2+z^2)}\geq \sum x^2+9$
$\Leftrightarrow 2\sum \sqrt{(x^2+y^2)(y^2+z^2)}\geq \sum x^2+(\sum x)^2$
$\Leftrightarrow \sum \sqrt{(x^2+y^2)(y^2+z^2)}\geq \sum x^2+\sum xy$
Mặt khác cũng theo bất đẳng thức Cauchy-Schwarz ta có;
$\sum \sqrt{(x^2+y^2)(y^2+z^2)}\geq \sum \sqrt{(\sqrt{y^2.y^2}+\sqrt{x^2.z^2})^2}= \sum x^2+\sum xy$
Như vậy ta được:P $\leq \frac{15}{4}$
Dấu ''='' xảy ra khi x=y=z=1
Nothing in your eyes
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: tìm giá trị lớn nhất
 
|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
tìm giá trị lớn nhấtBắt đầu bởi nguyenducthanh, 13-10-2022 |
|

|
|
 
|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
Tìm giá trị lớn nhấtBắt đầu bởi nguyenducthanh, 17-06-2021 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
Tìm giá trị lớn nhất của biểu thức $Q=a^{2}(b-c)+b^{2}(c-b)+c^{2}(1-c)$Bắt đầu bởi doremon01, 06-06-2016 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
Tìm giá trị lớn nhất $P=\sum\frac{1}{3x+3y+2z}$Bắt đầu bởi ndt063, 29-01-2016 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
Tìm giá trị lớn nhất M=a$ \sqrt{3a(a+2b)+b\sqrt{3a(b+2a)}}$Bắt đầu bởi daikixendopro, 18-11-2014 |
|

|
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh