Chủ đề này có 5 trả lời

[qtvc]

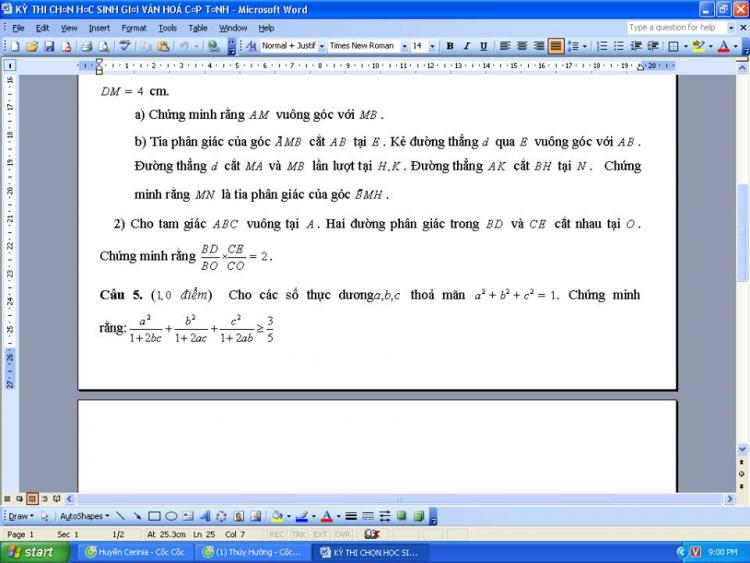
Câu 5 (trong đề).

Hình gửi kèm

• 

[qtvc]

Bài 2: Tìm tất cả các số nguyên n để n⁴ + 3n³ +3n² là số chính phương.

[royal1534]

Câu 5 (trong đề).

Vì $a^2+b^2+c^2=1$ nên ta viết lại bđt cần chứng minh thành:

$\sum \frac{a^2}{a^2+b^2+c^2+2bc} \geq \frac{3}{5}$

$\leftrightarrow \sum \frac{a^2}{a^2+(b+c)^2} \geq \frac{3}{5}$

Sử dụng bđt AM-GM ta có:

$\sum \frac{a^2}{a^2+(b+c)^2}  \geq \sum \frac{a^2}{a^2+2(b^2+c^2)}$

Ta quy bài toán về chứng minh:

$\sum \frac{a^2}{a^2+2(b^2+c^2)} \geq \frac{3}{5} (1)$

Để đơn giản ta đặt $(a^2,b^2,c^2)=(x,y,z)$

$(1) \leftrightarrow \sum \frac{x}{x+2(y+z)} \geq \frac{3}{5}$

Sử dụng bđt Cauchy-Swarchz ta có:

$VT=\sum \frac{x}{x+2(y+z)}=\sum \frac{x^2}{x^2+2xy+2xz}  \geq \frac{(x+y+z)^2}{x^2+y^2+z^2+4(xy+yz+zx)}$

Vậy ta cần chứng minh $\frac{(x+y+z)^2}{x^2+y^2+z^2+4(xy+yz+zx)} \geq \frac{3}{5}$

Thực hiện phép khai triển .BĐT trên $\leftrightarrow (x-y)^2+(y-z)^2+(z-x)^2 \geq 0$:Đúng

Ta có đpcm.Đẳng thức xảy ra khi $x=y=z$ hay $a=b=c=\frac{1}{\sqrt{3}}$

Bài viết đã được chỉnh sửa nội dung bởi royal1534: 08-03-2016 - 23:02

[royal1534]

Bài 2: Tìm tất cả các số nguyên n để n⁴ + 3n³ +3n² là số chính phương.

Đặt $A=n^4+3n^3+3n^2$

$\Rightarrow  4A=4n^4+12n^3+12n^2$

Nếu $n=0 \Rightarrow A=0$:Là số chính phương 

Với $n \neq 0$

Ta có $4n^4+13n^2+12n^3+6n+1>4n^4+12n^3+12n^2>4n^4+12n^3+9n^2$

$\Rightarrow (2n^2+3n+1)^2>4A>(2n^2+3n)^2$

$\Rightarrow 4A$ không thể là số chính phương 

$\Rightarrow A$ không là số chính phương

Vậy với $n=0$ thì $A=n^4+3n^3+3n^2$ là số chính phương

[qtvc]

Hình như bạn làm sai đoạn dưới này rồi, còn ra hai đáp án nữa là -2 với -1 nữa.

 

Ta có $4n^4+13n^2+12n^3+6n+1>4n^4+12n^3+12n^2>4n^4+12n^3+9n^2$

 

Trong đoạn này 6n + 1 chưa chắc đã lớn hơn 0 đâu, n nguyên mà.

[KietLW9]

Áp dụng Bunyakovsky dạng phân thức: $\frac{a^2}{1+2bc}+\frac{b^2}{1+2ca}+\frac{c^2}{1+2ab}=\frac{a^4}{a^2+2a^2bc}+\frac{b^4}{b^2+2ab^2c}+\frac{c^4}{1+2abc^2}\geqslant \frac{(a^2+b^2+c^2)^2}{(a^2+b^2+c^2)+2abc(a+b+c)}\geqslant \frac{(a^2+b^2+c^2)^2}{(a^2+b^2+c^2)+2.\frac{(a^2+b^2+c^2)^2}{3}}=\frac{3}{5}$

Bài viết đã được chỉnh sửa nội dung bởi KietLW9: 08-05-2021 - 16:58