Như vậy lời giải cho hai bài Tuần 5, tháng 8, 2017 đã được đưa tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng và anh Nguyễn Tiến Dũng. Xin được trích dẫn lại hai bài toán:
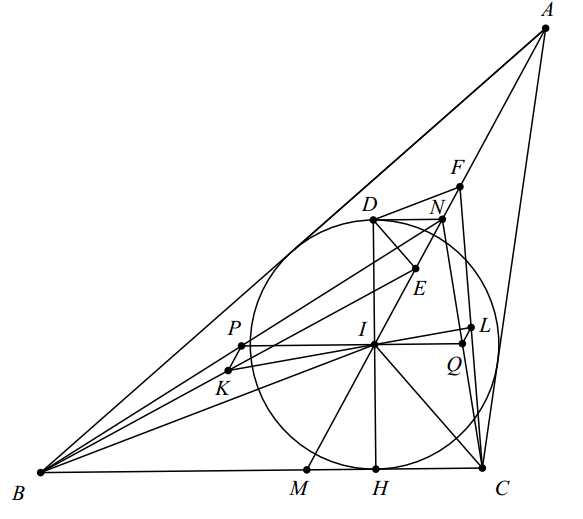
Bài 1. Cho tam giác $ABC$ nhọn nội tiếp trong đường tròn $(O)$. $M$ là trung điểm $BC$. Tiếp tuyến qua $B,C$ của $(O)$ cắt nhau tại $T$. Trên $TB,TC$ lấy các điểm $F,E$ sao cho $MF \parallel AB, ME \parallel AC$. $TM$ cắt $EF$ tại $D$. $ME,MF$ lần lượt cắt các đường tròn ngoại tiếp tam giác $TED, TFD$ tại $N,P$ khác $E,F$. $OE,OF$ lần lượt cắt $TN,TP$ tại $Q,R$. $S$ đối xứng $T$ qua $QR$. Chứng minh rằng đường tròn ngoại tiếp tam giác $SEF$ tiếp xúc $(O)$.
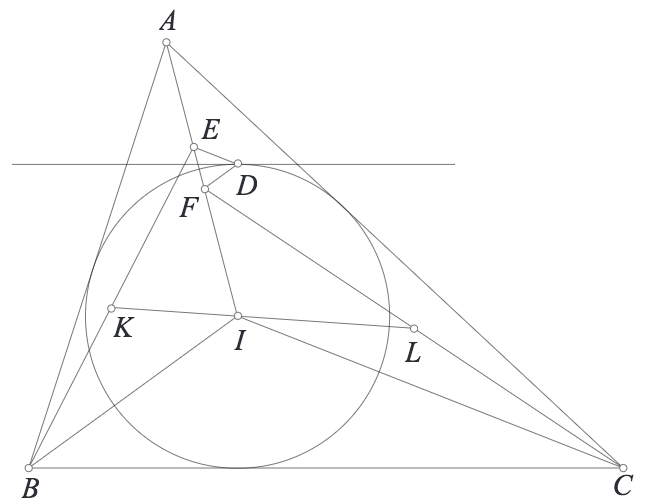
Bài 2. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$. Tiếp tuyến của $(I)$ song song với $BC$ tiếp xúc $(I)$ tại $D$> Lấy các điểm $E,F$ trên $IA$ sao cho $DE \parallel IC$ và $DF \parallel IB$. Chứng minh rằng đường thẳng nối trung điểm các đoạn thẳng $BE,CF$ đi qua $I$.