Chủ đề này có 452 trả lời

[BlackSelena]

Bài 32 (lớp 9): Cho đường tròn tâm $O$, đường kính $AB = 13$. Dây $CD = 12$ vuông góc với $AB$ tại $H$.
a, Tính $HA,HB$
b, Gọi $M,N$ theo thứ tự là hình chiếu của $H$ trên $AC,BC$. Tính $S_{CMHN}$

[henry0905]

Bài 32 (lớp 9): Cho đường tròn tâm $O$, đường kính $AB = 13$. Dây $CD = 12$ vuông góc với $AB$ tại $H$.
a, Tính $HA,HB$
b, Gọi $M,N$ theo thứ tự là hình chiếu của $H$ trên $AC,BC$. Tính $S_{CMHN}$

Ta có: HC=HD=6
HC.HD=HA.HB=36
Mà HA+HB=13
vây HA,HB là nghiệm của PT: $x^{2}-13x+36=0$
HA=4,HB=9

Bài viết đã được chỉnh sửa nội dung bởi henry0905: 15-07-2012 - 11:32

[henry0905]

Bài 33 (dựng hình): Dựng tam giác ABC biết cạnh BC=a, AC=b và $\widehat{A}-\widehat{B}=\alpha $

[triethuynhmath]

Tiếp lời câu b:
Theo lời giải câu a của bạn henry0905,ta có :
HA=4,HC=9=> $AC^2=AH.AB=4.13=> CA=2\sqrt{13}(cm)$
$CB^2=BH.AB=9.13=117(cm)=> CB=3\sqrt{13}(cm)$
Ta có: $CM=\frac{CH^2}{CA}=\frac{36}{2\sqrt{13}}=\frac{18\sqrt{13}}{13}(cm)$
$CN=\frac{CH^2}{CB}=\frac{36}{3\sqrt{13}}=\frac{12\sqrt{13}}{13}(cm)$
=> $CMHN=CM.CN=\frac{216}{13}(cm^2)$

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 15-07-2012 - 11:43

[BlackSelena]

Cách khác ngắn và sẽ áp dụng được nhiều hơn cho câu b.
Ta chứng minh công thức sau:
Cho tam giác $ABC: \text{ vuông tại A }$. Đường cao $AH (H \epsilon BC)$, $HE \perp AB; HD \perp AC$. Ta sẽ chứng minh
$S_{ADHE} = \frac{AH^3}{BC}$
Thật vậy, có $S_{ADHE} = AE.AD = \frac{AH^2}{AB} . \frac{AH^2}{AC} = \frac{AH^4}{AB.AC} = \frac{AH^4}{BC.AH}$
Áp dụng công thức này vào thẳng bài kia.
$S_{CMHN} = \frac{6^3}{13} = \frac{216}{13}$

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 15-07-2012 - 12:02

[Beautifulsunrise]

Bài 34 (Lớp 8): Cho tam giác ABC có AM, BN là các đường trung tuyến và AD, BE là các đường phân giác.
a) Nếu $\angle A > \angle B$ thì AM < BN và AD < BE.
b) Nếu AD = BE thì tam giác ABC cân.

[defaw]

Bài 34 (Lớp 8): Cho tam giác ABC có AM, BN là các đường trung tuyến và AD, BE là các đường phân giác.
a) Nếu $\angle A > \angle B$ thì AM < BN và AD < BE.

Bài 34:

a)Ta có: $BE^2=BC\cdot BA - EC\cdot EA$ và $AD^2=AB\cdot AC - DB\cdot DC$.
Ta cần chứng minh $a>b$ thì $AD<BE$, tương đương với
$AB\cdot AC - DB\cdot DC < BC\cdot BA - EC\cdot EA$
$\Leftrightarrow bc - \frac{bca^2}{(b+c)^2} < ac - \frac{acb^2}{(a+c)^2}$ (*)
Ta có: $ac > bc$ và $(a+c)^2>(b+c)^2$; $bca^2>acb^2$ nên ta có (*)
Vậy $AD < BE$.

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 16-07-2012 - 21:05

[henry0905]

Bài 31: Cho tam giác ABC, M là điểm nằm trong tam giác. Các tia AM, BM, CM cắt BC, CA, AB lần lượt lại D,E,F. CMR: $S_{DEF}\leq \frac{1}{4}S_{ABC}$. Dấu = xảy ra khi nào?

Bài 31: http://diendantoanho...showtopic=70674

Bạn có nhầm lẫn không? Bài mình là về diện tích, còn bài bạn post là chu vi, với lại dấu = là chân 3 đường cao cũng không chính xác.
__________________________________
C.X.Huy: Sorry nhầm cái đề
----------------------------
@binhmetric: Mình đã sửa lại đề theo như bên dưới, có chỗ nào không phải mong người ra đề chỉnh lại cho phải dùm nhá.

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 16-07-2012 - 21:13

[defaw]

Bài 31: Cho tam giác ABC, D,E,F là 3 điểm bất kì thuộc BC,CA,AB. C/m $S_{DEF}\leq \frac{1}{4}S_{ABC}$. Dấu = xảy ra khi nào?


Bạn có nhầm lẫn không? Bài mình là về diện tích, còn bài bạn post là chu vi, với lại dấu = là chân 3 đường cao cũng không chính xác.

Em nghĩ là cho các điểm này chạy ra sát với các đỉnh $\triangle ABC$ thì
$S_{DEF} > \frac{1}{4}S_{ABC}$.

Bài viết đã được chỉnh sửa nội dung bởi defaw: 15-07-2012 - 19:27

[BlackSelena]

Em nghĩ là cho các điểm này chạy ra sát với các đỉnh $\triangle ABC$ thì
$S_{DEF} > \frac{1}{4}S_{ABC}$.

Còn theo mình đề đúng là:
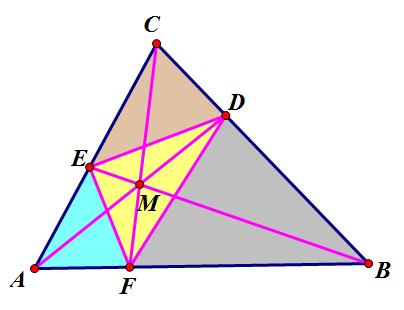
Cho $\triangle ABC$, $M$ là 1 điểm bất kì nằm trong tam giác $AM \cap BC = D, BM \cap AC = E, CM \cap AB = F$
CMR : $S_{DEF} \leq \frac{1}{4}S_{ABC}$

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 16-07-2012 - 21:16

[henry0905]

Em nghĩ là cho các điểm này chạy ra sát với các đỉnh $\triangle ABC$ thì
$S_{DEF} > \frac{1}{4}S_{ABC}$.

Bạn Selena nói đúng. Sorry bạn, mình đã sửa lại đề.

[tolaphuy10a1lhp]

Bài 35:[Câu 2: (THCS) - VMF 2011 - ĐỀ THI CHO TRẬN BETA - DELTA]
Cho hình thang có diện tích bằng 1. Hỏi đường chéo hình thang có thể lấy giá trị nhỏ nhất là bao nhiêu.
-------------
Bài này khá hay, mà chưa có ai giải, mình nghĩ các bạn xem qua.

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 16-07-2012 - 21:17

[BlackSelena]

Bài 36 (lớp 9):
Cho $\triangle ABC$, $I$ là tâm đường tròn nội tiếp. $I'$ là tâm đường tròn bàng tiếp góc $A$.
$AB=c,AC=b,BC=a$
a) $AI.AI'= b.c$
b) Đường thẳng qua $I' \perp AI'$ cắt $AC$ ở $E$
CMR: $AE= \frac{b.c}{p-a}$ (p là nửa chu vi)
c) $H,K$ là hình chiếu vuông góc của $I'$ lên $AB,AC$
$L$ thuộc $HK$ sao cho $CL// AB$
Cm: $B,L,E$ thẳng hàng.
2 - 3 ngày nữa em sẽ post lời giải

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 16-07-2012 - 23:23

[triethuynhmath]

Chém câu a trước,ta có $\angle BAI'=\angle IAC$
Ta có:
$\angle AIC=90^0+\frac{\angle B}{2}=90^0+\angle ABI=\angle ABI'$
=> Tam giác ABI' đồng dạng tam giác AIC(gg)=> AI.AI'=AB.AC=bc(Q.E.D)

[henry0905]

Bài 36 (lớp 9):
Cho $\triangle ABC$, $I$ là tâm đường tròn nội tiếp. $I'$ là tâm đường tròn bàng tiếp góc $A$.
$AB=c,AC=b,BC=a$
a) $AI.AI'= b.c$
b) Đường thẳng qua $I' \perp AI'$ cắt $AC$ ở $E$
CMR: $AE= \frac{b.c}{p-a}$ (p là nửa chu vi)
c) $H,K$ là hình chiếu vuông góc của $I'$ lên $AB,AC$
$L$ thuộc $HK$ sao cho $CL// AB$
Cm: $B,L,E$ thẳng hàng.
2 - 3 ngày nữa em sẽ post lời giải

Vẽ IK vuông góc AC tại K
Ta có: $\triangle AIK\sim \triangle AEI'$
$\Rightarrow AK.AE=AI.AI'=b.c$
Dễ dàng c/m K thuộc (I) nên $AK=\frac{b+c-a}{2}$ (dpcm)

Bài viết đã được chỉnh sửa nội dung bởi henry0905: 17-07-2012 - 12:53

[BlackSelena]

Chém nhanh quá ha .
Em gợi ý câu c: Dùng menelaus đảo.

 

triethuynhmath:$AK=\frac{b+c-a}{2}$ chứ chú !!!

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 22:55

[triethuynhmath]

Chém cho hết bài 36:
c)Ta có theo câu b,ta có:(Mình cho (I) tiếp xúc AB tại D)
$AD.AE=(p-a).AE=AB.AC$
$CL//AB$ nên áp dụng định lí Thales,ta được:
$\frac{KL}{LH}=\frac{KC}{AC}$
Đến khúc này mệt mỏi đây:
Ta có: $\angle HBI'=\angle \frac{HBC}{2}=\angle \frac{A+C}{2}=\angle IAC+\angle ICA=\angle I'IC$
=> Tam giác I'HB đồng dạng tam giác I'CI(gg)
=> $\frac{BH}{HI'}=\frac{IC}{CI'}$
Ta có $\angle ICH=90^0=> \angle ICD+\angle I'CK=90^0=> \angle ICK=\angle DIC$
=> tam giác IDC đồng dạng tam giác CKI'(gg)
=> $\frac{IC}{CI'}=\frac{ID}{CK}$=> $\frac{BH}{HI'}=\frac{ID}{CK}=>BH.CK=HI'.ID=KI'.ID$(t/c đường tròn bàng tiếp)
DDCM tam giác ADI đồng dạng tam giác I'KE($\angle KI'E=I'AE$)
=>$AD.KE=ID.I'K=BH.CK$
=>$AD=\frac{BH.CK}{KE}$
Đến đây đơn giản rồi:
Trong tam giác HKA,ta có
$\frac{BH}{AB}.\frac{EA}{EK}.\frac{KL}{LH}=\frac{BH}{AB}.\frac{EA}{EK}.\frac{CK}{AC}$
$=\frac{EA}{AB.AC}.\frac{BH.CK}{EK}=\frac{EA}{AB.AC}.AD=\frac{AE.AD}{AB.AC}=1$
=> B,L,E thẳng hàng(Menelaus đảo)

[tkvn97]

Bài 35:[Câu 2: (THCS) - VMF 2011 - ĐỀ THI CHO TRẬN BETA - DELTA]
Cho hình thang có diện tích bằng 1. Hỏi đường chéo hình thang có thể lấy giá trị nhỏ nhất là bao nhiêu.
-------------
Bài này khá hay, mà chưa có ai giải, mình nghĩ các bạn xem qua.

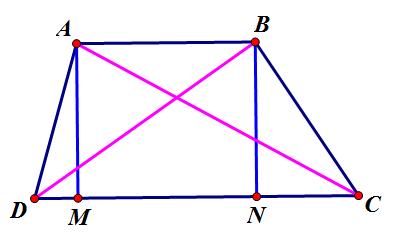
Giả sử hình thang ABCD có diện tích bằng 1 .
Đặt $AC = d_{1} , BD = d_{2}$
Kẻ AM vuông góc CD , BN vuông góc với CD . Đặt Mc = x , ND = y thì x ,y tương ứng là hình chiếu của $d_{1}$ và $d_{2}$ trên CD .
Giả sử $d_{1}\geq d_{2}\Rightarrow x\geq y$
Ta có $2x\geq x+y = MC + ND = DC + MN$
Dễ thấy MN = AB nên $2x\geq x+y=CD+AB$
Trong tam giác vuông AMC , có $AC^{2}=AM^{2}+MC^{2}\geq 2AM. MC \Leftrightarrow d_{1}^{2}=h^{2}+x^{2}\geq 2x.h$ trong đó h = AM là đường cao của hình thang .
Mặt khác $2x.h \geq (CD+AB)h = 2S_{ABCD} \Rightarrow d_{1}^{2}\geq 2\Rightarrow d_{1}\geq \sqrt{2}$
Vậy đườg chéo lớn nhất cua hình thang có độ dài nhỏ nhất là $\sqrt{2}$

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 19-07-2012 - 23:10

[tkvn97]

Mình post mấy bài khá hay cho anh em cùng chém nhé.
Bài 37 .
Cho tam giác ABC . Đường tròn $(O_{1})$ qua A tiếp xúc với BC tại C . Đường tròn $(O_{2})$ qua B tiếp xúc với AC tại C . Đường tròn $(O_{1})$ cắt $(O_{2})$ tại điểm thứ hai P . Gọi $O, R$ lần lượt là tâm . bán kính đường tròn ngoại tiếp tam giác ABC . Chứng minh:
a) $CP\leq R$
b) CP đi qua một điểm cố định khi C thay đổi trên đường tròn $©$
Bài 38 .
Cho đường tròn tâm O và dây cung AB cố định $(O\notin AB)$ . P là điểm di động trên đoạn thẳng ( AB $P \neq A , B$ và P khác trung điểm AB ) Đường tròn tâm C đi qua P tiếp xúc với đường tròn O tại A . Đường tròn tâm D đi qua P tiếp xúc với đường tròn (O) tại B . Hai đường tròn © và (D) cắt nhau tại N $(N\neq P)$.
a) Chứng minh rằng $\widehat{ANP } = \widehat{BNP}$ vfa bốn điểm O , D , C , N cùng nằm trên một đường tròn .
b) Chứng minh rằng đường trung trực của đoạn ON luôn đi qua một điểm cố định khi P di động.

Bài viết đã được chỉnh sửa nội dung bởi TRUNGKIEN1997: 17-07-2012 - 15:46

[henry0905]

Bài 37 .
Cho tam giác ABC . Đường tròn $(C_{1})$ qua A tiếp xúc với BC tại C . Đường tròn $(C_{2})$ qua B tiếp xúc với AC tại C . Đường tròn $(C_{1})$ cắt $(C_{2})$ tại điểm thứ hai P . Gọi $C , R$ lần lượt là tâm . bán kính đường tròn ngoại tiếp tam giác ABC . Chứng minh:
a) $CP\leq R$

Một bài toán mà có 2 điểm C?
a) Nếu C là tam đường tròn ngoại tiếp tam giác ABC, đổi thành O
Nếu tam giác ABC nhọn thì $OP\leq R$
Nếu tam giác ABC tù thì $OP> R$

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 19-07-2012 - 23:24